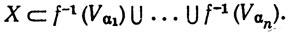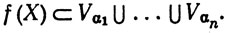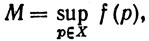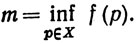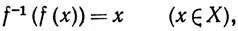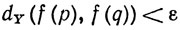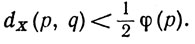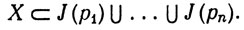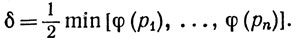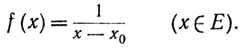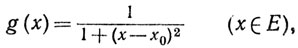Доказать что отображение непрерывно

Введение в топологические пространства. Программирование конечных топологий на Java. Часть 2: База топологии. Непрерывные отображения

Введение

Прежде, чем мы пойдём дальше, я бы хотел задать вам следующий простой вопрос.

Упражнение 0. Пусть X — множество из n элементов. Сколько элементов содержит дискретная топология т, содержащая все подмножества множества X?

Но с помощью базы вам достаточно задать всего лишь 10 множеств вместо 1024. А если у вас топология не дискретная, то и того меньше.

Итак, перейдём к определению. Существует несколько эквивалентных определений базы топологии. Я приведу как основное то определение, которое используется в колмогоровской школе, а затем докажу эквивалентность другого определения.

Определение 1. Совокупность J открытых подмножеств множества X называется базой топологии, если всякое открытое подмножество G пространства (X, т) может быть представлено как объединение некоторого набора множеств из J.

С математической точки зрения это определение вполне понятно, однако запрограммировать его является достаточно нетривиальной задачей. Ситуацию усложняет и то, что множество G не обязано быть объединением двух множеств базы, оно может быть объединениём и трёх, и четырёх, и так далее.

К счастью, дело поможет упростить следующая теорема.
Теорема 1. Для того, чтобы система J была базой топологии, необходимо и достаточно, чтобы для каждого открытого множества G и для каждой точки x из G существовало такое множество G(x), принадлежащее J и содержащее x, что G(x) является подмножеством G.

Доказательство теоремы также достаточно простое. Сперва докажем достаточность условия. Это означает, что если выполнено написанное условие, то J будет базой топологии.
Но если оно выполнено, то G можно представить как объединение по всем x из G множеств G(x), т. е. выполнено условие из определения, и J — база топологии.
Необходимость условия означает то, что если J — база, то верно наше условие. Но если J — база, то любое открытое множество представимо в виде объединения множеств из J, откуда немедленно вытекает условие.

Эта теорема уже лучше помогает запрограммировать алгоритм определения, является ли базой данная система подмножеств, однако некоторую сложность здесь представляет то, что первым квантором условия является квантор всеобщности.

А это означает, что при проектировании алгоритма мы должны идти от обратного: сперва считаем, что наша система база, и меняем решение, если выполнено обратное утверждение.

В математике обращение таких условий происходит следующим образом: квантор всеобщности заменяется на квантор существования и наоборот, а предикат заменяется на обратный.

Поэтому алгоритм, записанный на естественном языке, будет звучать следующим образом:

1. Считаем, что аргумент метода является базой топологии.
2. Если существует такое открытое множество G и такая точка x из G, что любое множество G из аргумента метода, содержащее x, НЕ явлется подмножеством G, то вернуть ЛОЖЬ, иначе вернуть ИСТИНУ.

Теперь создадим небольшой класс для базы

Это необходимо для того, чтобы иметь возможность написать конструктор топологии по базе.

А дополнить систему до топологии достаточно легко, только допишем несколько приватных методов. Но прежде, простые задачки.

Задача 1. Пусть X — множество мощности n, а т — дискретная топология, заданная на этом множестве. Найти базу топологии.

Если говорить об общей топологии, то довольно важным классом топологических пространств являются пространства со счётной базой. Их также называют пространствами со второй аксиомой счётности.

Легко заметить, что конечные топологические пространства, а именно их мы и программируем, образуют подмножество всех пространств со второй аксиомой счётности.

Но если это вторая аксиома счётности, то должна быть и первая, не так ли? Ею мы сейчас и займёмся, а затем окунёмся в непрерывные отображения.

Определяющие системы окрестностей

Определение 2. Пусть для точки x топологического пространства X существует не более, чем счётная система окрестностей n(x)> такая, что для всякого открытого множества G, содержащего x, найдётся окрестность O_n(x), содержащаяся в G. Эта система называется определяющей системой окрестностей точки x.

Определение 3. Если для каждой точки x существует её определяющая система окрестностей, то пространство удовлетворяет первой аксиоме счётности.

Это определение представляет больший интерес в рамках общей топологии, чем в рассматриваемых сейчас конечных топологиях, поскольку в качестве такой системы можно просто взять систему всех окрестностей данной точки. Однако, даже здесь можно поставить один интересный вопрос, который я любезно предоставлю Вам.

Задача 3. Привести пример конечного топологического пространства, в котором определяющая система окрестностей какой-либо точки лежит строго внутри системы всех окрестностей данной точки.

Система <<3>> является определяющей системой окрестности точки 3.

Непрерывные отображения

Вот мы и подошли к самому интересному месту нашей сегодняшней лекции. К непрерывным отображениям.

В принципе, в Java уже есть интерфейс для отображений: Mapper, однако из-за того, что он содержит два метода, он не может быть использован в качестве функционального интерфейса.

Я использую Java 8, и мне бы хотелось писать отображения в более удобном виде, чем создавать класс, имплементирующий интерфейс и так далее. Если Ваша среда разработки не поддерживает Java 8, то код метода всё равно будет работать, а вот код вызова придётся поменять.

Итак, я создам следующий простенький интерфейс

Аннотация выше необязательна, но она даст ошибку, если добавить в интерфейс ещё один абстрактный метод.

Теперь перейдём к математической стороне вопроса и дадим понятие непрерывности в терминах окрестностей точки.

Определение 4. Пусть (X, т1) и (Y, т2) — два топологических пространства. Отображение f пространства X в пространство Y называется непрерывным в точке x₀, если для любой окрестности U_y0 точки y₀ = f(x₀) найдётся такая окрестность V_x0 точки x₀, что f( V_x0) содержится внутри U_y0. Отображение f называется непрерывным, если оно непрерывно в каждой точке.

Если это перевести на русский язык, то определение непрерывности в точке звучать будет примерно так: Какую бы окрестность образа данной точки мы не взяли, найдётся окрестность данной точки, что образ этой окрестности будет лежать внутри окрестности образа точки.

Минуточку… Если вспомнить начала анализа, то мы получим в точности определение непрерывности функции по Коши, с той лишь разницей, что мы ушли от эпсилон-дельта языка и заменили отношение частичного порядка в определении близости.

Но не всё так просто здесь. Поэтому я предлагаю вам интересную задачку.
Задача 4. Пусть X — топологическое пространство с базой <<1>,<2,4>,<1,2,3,4>>, Y — с базой <<1>,<3>,<1,2,3,4>>.
Рассмотрим тождественное отображение f из X в Y, действующее по правилу f(x) = x. Является ли оно непрерывным? Если да, то докажите это. Если нет, покажите, в какой точке оно терпит разрыв.
Такой же вопрос и для отображения f из Y в X, действующего по правилу f(x) = x.

На этот раз я приведу вам и код исполнения:

Как вы видите, использование лямбда-выражения здесь довольно оправдано, поскольку позволяет достаточно точно задать правило отображения одного пространства в другое.

И, как я обещал, ответ:

Заключение
Сегодня мы познакомились с важным понятием базы топологии и научились строить по ней всю топологию пространства. Мы узнали про аксиомы счётности и то, что конечные топологии удовлетворяют обеим аксиомам счётности.

В следующей части я планирую рассказать чуть побольше об отображениях топологических пространств, ввести понятие открытого и замкнутого отображения, а также дать признак непрерывности отображения, который будет проще, чем изложенный в определении и перейти к новой теме: аксиомам отделимости.

В конце этого цикла статей я также планирую дать какой-либо практический пример применения конечной топологии. Спасибо за внимание!

Источник

Доказать что отображение непрерывно

Равносильное определение: непрерывным называется отображение, при котором прообразы замкнутых множеств замкнуты.

Упражнение. Проверьте эквивалентность двух определений непрерывного отображения.

Также нам потребуется определение отображения, непрерывного в точке.

Числовая прямая является метрическим пространством с метрикой вида поэтому, выбрав окрестности точек в виде открытых шаров (которые в данном случае являются открытыми интервалами), получим определение функции, непрерывной в точке.

Можно доказать, что отображение топологических пространств непрерывно тогда и только тогда, когда оно непрерывно в каждой точке.

Теперь обратимся к простейшим свойствам непрерывных отображений топологических пространств.

Теорема 1. Тождественное отображение топологического пространства в себя непрерывно.

Теорема 3. Отображение вложения подпространства в топологическое пространство непрерывно.

Теорема 4. Композиция непрерывных отображений топологических пространств непрерывна.

Для доказательства рассмотрим непрерывные отображения топологических пространств и и их композицию

Теперь обратимся к понятию категории.

Для любого неодноточечного пространства постоянное отображение не является гомеоморфизмом (оно не взаимно однозначно и тем более не обратимо).

Приведем примеры гомеоморфных топологических пространств, известных из других курсов геометрии.

Обратное отображение плоскости на параболоид имеет вид:

Оба отображения заданы непрерывными функциями и, следовательно, непрерывны, что и доказывает гомеоморфизм.

2. Трехосный эллипсоид гомеоморфен сфере.

Каноническое уравнение трехосного эллипсоида имеет вид:

Уравнение сферы с центром в начале координат: Отображение эллипсоида на сферу, осуществляющее гомеоморфизм, задается в координатах следующим образом:

Аналогично, в силу непрерывности обратного отображения прообраз при отображении любого открытого в множества также открыт:

Доказанное означает, что если некоторое топологическое утверждение верно для одного из двух гомеоморфных топологических пространств, то такое же утверждение верно для другого. Гомеоморфные пространства топологически неразличимы, поэтому о них говорят, что они имеют один топологический тип.

Отношение гомеоморфности в классе топологических пространств рефлексивно, симметрично и транзитивно, то есть является отношением эквивалентности (докажите!)

Топологические пространства могут быть негомеоморфными, но локально гомеоморфными. Таковы, например, тор (компактное пространство) и евклидова плоскость (некомпактное пространство.)

Источник

Доказать что отображение непрерывно

1.5.4. Непрерывные отображения

Понятие топологии является минимально необходимым для того, чтобы говорить о непрерывных отображениях в ощем случае. Интуитивно непрерывность есть отсутствие разрывов, то есть близкие точки при непрерывном отображении должны переходить в близкие. Оказывается, для определения понятия близости точек можно обойтись без понятия расстояния. Именно это и есть топологическое определение непрерывного отображения.

Определение 1. Точкой топологического пространства T = (x,τ) называют любой его элемент.

Определение 2.Окрестностью точки в топологическом пространстве называется любое открытое множество, содержащее указанную точку.

Определение 3. Для любого топологического пространства множество A⊂T = (X,τ) называется открытым если каждая точка x∈A имеет окрестность U_x⊂A.

Пусть задано отображение F:X→Y и A⊂X.

Определение 4. Множество F(A):y:=F(x), x⊂A, y⊂Y где называется образом множества А при отображении F.

Определение 7. Отображение, непрерывное в каждой точке x множества X, называется непрерывным на X. Если множество X фиксировано, отображения называют просто непрерывными, не указывая X.

Определение 8. Отображение топологических пространств называется непрерывным, если прообраз всякого открытого множества открыт.

( Комментарий. Итак, при непрерывном отображении прообраз открытого отображения открыт, а замкнутого замкнут. Для образов при непрерывных отображениях такого рода утверждения, вообще говоря, не имеют место.)

Источник

Доказать что отображение непрерывно

Непрерывность и компактность

4.13. Определение. Отображение f множества Е в пространство R л называется ограниченным, если существует вещественное число М, такое, что 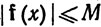для всех х∈Е.

Выведем теперь некоторые следствия из теоремы 4.14.

Тогда существуют точки p,q∈X, такие, что f(p) = M и f(q) = m.

Утверждение теоремы можно сформулировать и так: существуют точки р и q в X, такие, что f(q)≤f(х)≤f(р) для всех x∈Х, т. е. функция f достигает своего максимума (в точке р) и минимума (в точке а).

есть непрерывное отображение множества Y на X.

для всех р и q из X, для которых d_X (p, q) 0 и для каждой точки р множества X можно найти число δ>0, обладающее свойством, указанным в определении 4.5. Это δ зависит от ε и от р. Если же f равномерно непрерывна на X, то для каждого ε>0 можно найти одно число δ>0, которое годится для всех точек р множества X.

Очевидно, каждая равномерно непрерывная функция непрерывна. В случае компактных множеств эти два понятия, как показывает следующая теорема, равносильны.

Доказательство. Пусть ε>0. Поскольку f непрерывно, каждой точке р∈Х можно сопоставить положительное число φ(р), такое, что

Тогда δ>0. (Именно здесь существенна конечность покрытия, упоминаемого в определении компактности. Минимум конечного числа положительных чисел положителен, тогда как нижняя грань бесконечного множества положительных чисел вполне может оказаться равной нулю.)

(a) существует неограниченная функция, непрерывная на Е;

(b) существует ограниченная функция, непрерывная на Е, не имеющая максимума.

(с) Если, кроме того, множество Е ограничено, то существует непрерывная на Е функция, не являющаяся равномерно непрерывной.

Доказательство. Допустим сначала, что Е ограничено, так что существует предельная точка х0 множества Е, не содержащаяся в Е.

Эта функция непрерывна на Е (теорема 4.9), но, очевидно, не ограничена. Убедимся в том, что функция (21) не является равномерно непрерывной. Пусть ε>0 и δ>0 произвольны. Выберем точку х∈Е, такую, что |х-х₀| 0, функция f не является равномерно непрерывной на Е.

Функция g, заданная равенством

Источник

Предел отображения в метрическом пространстве

Содержание

Подмножества метрического пространства [ править ]

Окрестность точки в метрическом пространстве [ править ]

Примеры [ править ]

Предельная точка [ править ]

Пример(ы) [ править ]

Предел отображения [ править ]

Пример(ы) [ править ]

Предел сложного отображения [ править ]

Если [math]f[/math] имеет предел, то в ситуации общих МП:

Пусть также заданы отображения

[math]f: A \rightarrow B, \qquad g: B \rightarrow Z [/math]

[math] (f(x) \ne b \forall x \in A) [/math]

[math] b = \lim\limits_ f(x) \qquad d = \lim\limits_ g(y) [/math]

Пусть [math]z(x) = g(f(x)) [/math]

Итак, сложная фукнция от двух непрерывных — непрерывна.

Некоторые непрерывные отображения [ править ]

Полагаем в этом неравенстве [math] x_1 = x, x_2 = x_0 [/math] и обращаемся к определению непрерывного отображения:

[math] f(x_1) \le \rho(x_1, a) \le \rho(x_2, a) + \rho(x_2, x_1) [/math]

Дальнейшие рассуждения аналогичны предыдущему доказательству непрерывности.

[math] \Rightarrow [/math] :

[math] \Leftarrow [/math] :

[math] \delta [/math] можно найти для любого p значит прообраз открыт

Замечание: так как замкнутые множества являются дополнениями открытых, то отсюда напрямую следует, что прообраз замкнутого множества при непрерывном отображении замкнут.

Свойства непрерывных отображений. Определение компакта [ править ]

Докажем от противного.

Эта последовательность неограниченна и из нее нельзя выделить сходящуюся. Но К — компакт, получили противоречие с определением компакта.

То, что K — замкнутое, следует из основного характеристического свойства замкнутых множеств.[math]\triangleleft[/math]

Эти классы определены, т.к:

Равномерно непрерывные отображения [ править ]

Замечание: обратное в общем случае неверно.

Допустим, что это не так. Тогда, по логическому отрицанию: [math]\exists \varepsilon_0 \gt 0

\exists _\delta, _\delta \in K: \rho(_\delta, _\delta) \lt \delta ; \rho(f(_\delta), f(_\delta)) \ge \varepsilon_0; [/math]

т.к. K — компакт, т.е. в послед [math]‘_[/math] можно выделить сходящуюся подпоследовательность меньшую [math]\frac<1><‘_>[/math] следовательно стремящуюся к нулю.

[math]‘_> \rightarrow x\in K[/math]

Частный случай: [math][a,b]\subset \mathbb, f:[a,b]\rightarrow \mathbb[/math]

по т. Кантора f — равномерно и непрерывна на [math][a,b][/math] т.е.

[math]\forall \varepsilon \gt 0 \exists \delta \gt 0 : \left | \bigtriangleup x \right | \lt \delta ; x, x+ \bigtriangleup x \in [a,b] \rightarrow \left | f(x+ \bigtriangleup x)-f(x) \right |\lt \varepsilon [/math]

[math]f(A)\subset G_<1>\cup G_<2>[/math]

прообразы открытых множеств открыты, оба они входят в A, а значит A — не связно — противоречие.

Источник

• Популярная книга Круть доступна для чтения прямо сейчас на нашем сайте boochi.ru. Скачать книгу в формате FB2, TXT, PDF, EPUB бесплатно без регистрации. →