Доказать что отрезки соединяющие середины противоположных ребер тетраэдра пересекаются в одной точке

Доказать что отрезки соединяющие середины противоположных ребер тетраэдра пересекаются в одной точке

ТЕТРАЭДР. ВИДЫ ТЕТРАЭДРОВ

Тетраэдр является одним из простейших многогранников, гранями которого являются четыре треугольника. Его можно считать пространственным аналогом треугольника. Рассмотрим свойства треугольников и аналогичные им свойства тетраэдров.
Теорема 1. Биссектрисы треугольника пересекаются в одной точке – центре вписанной окружности.
Теорема 1′. Биссектральные плоскости двугранных углов тетраэдра пересекаются в одной точке – центре вписанной сферы.
Доказательство. Пусть ABCD – тетраэдр. Пересечением биссектральных плоскостей двугранных углов с ребрами AB, AC,и BC (рис. 1) является точка O, равноудаленная от всех граней тетраэдра. Следовательно, эта точка принадлежит биссектральным плоскостям остальных двугранных углов тетраэдра и является центром вписанной сферы.

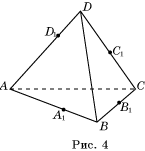
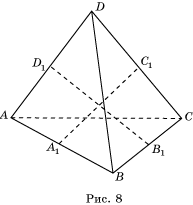
Теорема 9′ (Чевы). Пусть на ребрах AB, BC, CD и AD тетраэдра ABCD взяты соответственно точки A ₁ , B ₁ , C ₁ и D ₁. Плоскости ABC ₁ , BCD ₁ , CDA ₁ и DAB ₁ пересекаются в одной точке тогда и только тогда, когда

Рассмотрим теперь некоторые специальные тетраэдры.
Равногранным тетраэдром называется тетраэдр, у которого все грани равны.
Теорема 10. Для любого остроугольного треугольника существует равногранный тетраэдр, грани которого равны данному треугольнику.
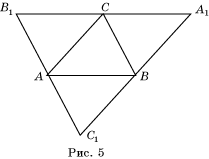
Доказательство. Пусть ABC – произвольный остроугольный треугольник. Через его вершины проведем прямые, параллельные противоположным сторонам (рис. 5).

Покажем обратное, пусть ABCD – равногранный тетраэдр, O – цетр описанной сферы. Тогда плоскости граней пересекают описанную сферу по окружностям одинакового радиуса. Следовательно, расстояния от точки O до граней тетраэдра равны и, значит O – центр вписанной сферы.
Прямоугольным тетраэдром называется тетраэдр, у которого все плоские углы при какой-нибудь вершине прямые.
Теорема 12. Основанием высоты прямоугольного тетраэдра, проведенной из вершины с прямыми плоскими углами, является точка пересечения высот противоположной грани.
Теорема 13. (Пифагора) Квадрат площади грани прямоугольного тетраэдра, лежащей против вершины с прямыми плоскими углами, равен сумме квадратов площадей остальных граней этого тетраэдра.
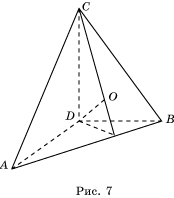
Доказательство. Пусть ABCD – прямоугольный тетраэдр (рис. 7). Плоские углы при вершине D прямые. Можно было бы обозначить ребра, выходящие из вершины D через a, b, c, а затем воспользоваться формулой Герона для нахождения площади треугольника ABC .

Тогда A ₁ B ₁ D ₁ C ₁ – параллелограмм. Его диагонали равны тогда и только тогда, когда он – прямоугольник, т.е. AC BD .
Теорема 2. Тетраэдр является ортогональным тогда и только тогда, когда он является ортоцентрическим.
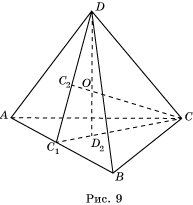
Доказательство. Пусть ABCD – ортогональный тетраэдр (рис. 9). DD ₂ – высота, опущенная из вершины D. Плоскость CDD ₂ перпендикулярна AB и, следовательно, DC ₁ и CC ₁ – высоты треугольников ABC и ABD. Высоты DD ₂ и CC ₂ треугольника C ₁ CD пересекаются.

Литература
1. Адамар Ж. Элементарная геометрия. Часть II. Стереометрия. – М.: Учпедгиз, 1938.
2. Перепелкин Д.И. Курс элементарной геометрии. Часть II. Геометрия в пространстве. – М.-Л.: Гостехиздат, 1949.
3. В.В.Прасолов, И.Ф.Шарыгин. Задачи по стереометрии. – М.: Наука, 1989.
4. Д.О.Шклярский, Н.Н.Ченцов, И.М.Яглом. Избранные задачи и теоремы элементарной математики. Часть 3. – М.: Государственное издательство технико-теоретической литературы, 1954.

Источник

Доказать что отрезки соединяющие середины противоположных ребер тетраэдра пересекаются в одной точке

а) Докажите, что медианы тетраэдра (отрезки, соединяющие вершины с точками пересечения медиан противоположных граней) и отрезки, соединяющие середины противоположных ребер, пересекаются в одной точке.

б) Дан тетраэдр с прямыми плоскими углами при вершине Площади граней и равны соответственно 132, 150, 539. Найдите объем тетраэдра.

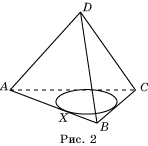
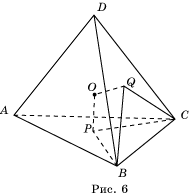
а) Пусть задан тетраэдр ABCD (рисунок 1)

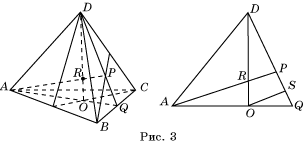
1. Рассмотрим грани ABC и ABD. Пусть M — точка пересечения медиан Δ ABC, N — треугольника ABD. И пусть K — середина AB. Точки C, D, M, N, K лежат в одной плоскости, коли они принадлежат двум пересекающимся прямым KC и KD. Поскольку KC : KM = KD : KN = 3 : 1, треугольники MKN и CKD гомотетичны с коэффициентом гомотетии (подобия) k = 3. По основному свойству гомотетии будем иметь: CD || MN, CD = 3MN.

Соединим отрезками точки: M и D, N и С. Точку пересечения MD с NC обозначим О.

Аналогично можно доказать, что через точку О пройдут все остальные медианы заданного тетраэдра.

2. Теперь докажем, что через точку О пройдут и отрезки, соединяющие середины противоположных ребер тетраэдра (рисунок 2).

Пусть L — середина ребра BC. В плоскости DKC через точку D проведем прямую, параллельную KC. Проведем также прямую KL, которая пересечет только что проведенную прямую в точке, которую обозначим P.

Пусть O₁ точка пересечения DM и KL.

Рассмотрим Δ KLC и Δ PLD. У них: ∠KLC = ∠PLD как вертикальные, ∠KCL = ∠ PDL как внутренние накрест лежащие при KC || PD и секущей DC, CL = DL. Тогда Δ KLC = Δ PLD — по второму признаку равенства треугольников. Отсюда: KC = PD, KL = PL, ∠CKL = ∠BPL.

В Δ KO₁M и Δ PO₁D ∠KO₁M = ∠ PO₁D как вертикальные, ∠MKO₁ = ∠DPO₁ по ранее доказанному. Значит, откуда DO₁ : O₁M = PD : KM. Но как доказано выше, KC = PD. Следовательно, O₁D : O₁M = KC : KM = 3 : 1.

Итак, O₁D : O₁M = 3 : 1. Выше было доказано, что OD : OM = 3 : 1. Так как отрезок DM можно разделить в отношении 3 : 1, считая от точки D, единственным образом, то точки О и O₁ совпадут, то есть KL проходит через точку О. Совершенно аналогично можно доказать то, что отрезки, соединяющие середины ребер BC и AD, BD и AC, пройдут через точку О. И это — все то, что требовалось доказать.

б) Введем обозначения длин ребер тетраэдра: пусть BD = a, CD = c, AD = b.

Источник

Доказать что отрезки соединяющие середины противоположных ребер тетраэдра пересекаются в одной точке

Докажите, что следующие свойства тетраэдра равносильны:

1) все грани равновелики;

2) каждое ребро равно противоположному;

4) центры описанной и вписанной сфер совпадают;

5) суммы углов при каждой вершине равны;

6) сумма плоских углов при каждой вершине равна 180 o ;

7) развёртка тетраэдра представляет собой остроугольный треугольник, в котором проведены средние линии;

8) все грани – остроугольные треугольники с одинаковым радиусом описанной окружности;

9) ортогональная проекция тетраэдра на каждую из трёх плоскостей, параллельных двум противоположным рёбрам, – прямоугольник;

10) параллелепипед, полученный в результате проведения через противоположные рёбра трёх пар параллельных плоскостей, – прямоугольный;

11) высоты тетраэдра равны;

12) точка пересечения медиан совпадает с центром описанной сферы;

13) точка пересечения медиан совпадает с центром вписанной сферы;

14) сумма плоских углов при трёх вершинах равна 180 o ;

15) сумма плоских углов при двух вершинах равна 180 o и два противоположных ребра равны.

Решение

Замечания

Рассмотрим следующие свойства тетраэдра (тетраэдром мы называем произвольную треугольную пирамиду):

i) все грани равновелики, то есть имеют одну и ту же площадь;

ii) каждое ребро равно противоположному;

iii) все грани равны;

iv) центры описанной и вписанной сфер совпадают;

v) для любой вершины тетраэдра сумма величин сходящихся в этой вершине плоских углов

Докажите, что все эти свойства эквивалентны. Постарайтесь найти другие эквивалентные им свойства тетраэдра.

Источник

Доказать что отрезки соединяющие середины противоположных ребер тетраэдра пересекаются в одной точке

а) Докажите, что медианы тетраэдра (отрезки, соединяющие вершины с точками пересечения медиан противоположных граней) и отрезки, соединяющие середины противоположных ребер, пересекаются в одной точке.

б) Дан тетраэдр с прямыми плоскими углами при вершине Площади граней и равны соответственно 132, 150, 539. Найдите объем тетраэдра.

1. Рассмотрим грани ABC и ABD. Пусть M — точка пересечения медиан Δ ABC, N — треугольника ABD. И пусть K — середина AB. Точки C, D, M, N, K лежат в одной плоскости, коли они принадлежат двум пересекающимся прямым KC и KD. Поскольку KC : KM = KD : KN = 3 : 1, треугольники MKN и CKD гомотетичны с коэффициентом гомотетии (подобия) k = 3. По основному свойству гомотетии будем иметь: CD || MN, CD = 3MN.

Соединим отрезками точки: M и D, N и С. Точку пересечения MD с NC обозначим О.

Аналогично можно доказать, что через точку О пройдут все остальные медианы заданного тетраэдра.

2. Теперь докажем, что через точку О пройдут и отрезки, соединяющие середины противоположных ребер тетраэдра (рисунок 2).

Пусть L — середина ребра BC. В плоскости DKC через точку D проведем прямую, параллельную KC. Проведем также прямую KL, которая пересечет только что проведенную прямую в точке, которую обозначим P.

Пусть O₁ точка пересечения DM и KL.

Рассмотрим Δ KLC и Δ PLD. У них: ∠KLC = ∠PLD как вертикальные, ∠KCL = ∠ PDL как внутренние накрест лежащие при KC || PD и секущей DC, CL = DL. Тогда Δ KLC = Δ PLD — по второму признаку равенства треугольников. Отсюда: KC = PD, KL = PL, ∠CKL = ∠BPL.

В Δ KO₁M и Δ PO₁D ∠KO₁M = ∠ PO₁D как вертикальные, ∠MKO₁ = ∠DPO₁ по ранее доказанному. Значит, откуда DO₁ : O₁M = PD : KM. Но как доказано выше, KC = PD. Следовательно, O₁D : O₁M = KC : KM = 3 : 1.

Итак, O₁D : O₁M = 3 : 1. Выше было доказано, что OD : OM = 3 : 1. Так как отрезок DM можно разделить в отношении 3 : 1, считая от точки D, единственным образом, то точки О и O₁ совпадут, то есть KL проходит через точку О. Совершенно аналогично можно доказать то, что отрезки, соединяющие середины ребер BC и AD, BD и AC, пройдут через точку О. И это — все то, что требовалось доказать.

б) Введем обозначения длин ребер тетраэдра: пусть BD = a, CD = c, AD = b.

Источник

Доказать что отрезки соединяющие середины противоположных ребер тетраэдра пересекаются в одной точке

а) Докажите, что медианы тетраэдра (отрезки, соединяющие вершины с точками пересечения медиан противоположных граней) и отрезки, соединяющие середины противоположных ребер, пересекаются в одной точке.

б) Дан тетраэдр с прямыми плоскими углами при вершине Площади граней и равны соответственно 132, 150, 539. Найдите объем тетраэдра.

а) Пусть задан тетраэдр ABCD (рисунок 1)

1. Рассмотрим грани ABC и ABD. Пусть M — точка пересечения медиан Δ ABC, N — треугольника ABD. И пусть K — середина AB. Точки C, D, M, N, K лежат в одной плоскости, коли они принадлежат двум пересекающимся прямым KC и KD. Поскольку KC : KM = KD : KN = 3 : 1, треугольники MKN и CKD гомотетичны с коэффициентом гомотетии (подобия) k = 3. По основному свойству гомотетии будем иметь: CD || MN, CD = 3MN.

Соединим отрезками точки: M и D, N и С. Точку пересечения MD с NC обозначим О.

Аналогично можно доказать, что через точку О пройдут все остальные медианы заданного тетраэдра.

2. Теперь докажем, что через точку О пройдут и отрезки, соединяющие середины противоположных ребер тетраэдра (рисунок 2).

Пусть L — середина ребра BC. В плоскости DKC через точку D проведем прямую, параллельную KC. Проведем также прямую KL, которая пересечет только что проведенную прямую в точке, которую обозначим P.

Пусть O₁ точка пересечения DM и KL.

Рассмотрим Δ KLC и Δ PLD. У них: ∠KLC = ∠PLD как вертикальные, ∠KCL = ∠ PDL как внутренние накрест лежащие при KC || PD и секущей DC, CL = DL. Тогда Δ KLC = Δ PLD — по второму признаку равенства треугольников. Отсюда: KC = PD, KL = PL, ∠CKL = ∠BPL.

В Δ KO₁M и Δ PO₁D ∠KO₁M = ∠ PO₁D как вертикальные, ∠MKO₁ = ∠DPO₁ по ранее доказанному. Значит, откуда DO₁ : O₁M = PD : KM. Но как доказано выше, KC = PD. Следовательно, O₁D : O₁M = KC : KM = 3 : 1.

Итак, O₁D : O₁M = 3 : 1. Выше было доказано, что OD : OM = 3 : 1. Так как отрезок DM можно разделить в отношении 3 : 1, считая от точки D, единственным образом, то точки О и O₁ совпадут, то есть KL проходит через точку О. Совершенно аналогично можно доказать то, что отрезки, соединяющие середины ребер BC и AD, BD и AC, пройдут через точку О. И это — все то, что требовалось доказать.

б) Введем обозначения длин ребер тетраэдра: пусть BD = a, CD = c, AD = b.

В соответствии с условием задачи:

В правильной шестиугольной пирамиде SABCDEF с вершиной S боковое ребро вдвое больше стороны основания.

а) Докажите, что плоскость, проходящая через середины рёбер SA и SE и вершину C, делит ребро SB в отношении 3 : 1, считая от вершины S.

б) Найдите отношение, в котором плоскость, проходящая через середины рёбер SA и SE и вершину C, делит ребро SF, считая от вершины S.

а) Обозначим середины ребер SA и SE за M и N соответственно. Прямая MN || AE, как средняя линия, и, следовательно, параллельна плоскости основания пирамиды. Это означает, что плоскость сечения пересекается с плоскостью основания по прямой a параллельной MN и проходящей через точку C. Пусть прямая AB пересекается с прямойa в точке P. Тогда точка P является одновременно точкой сечения и плоскости SAB. Пусть прямая MP пересекает ребро SB в точке K. Требуется доказать, что SK : KB = 3 : 1. Рассмотрим плоскость SAB, в соответствующем треугольнике проведем среднюю линию MM’ || AB. Заметим теперь, что из свойств правильного шестиугольника отрезок Таким образом, треугольники MM’K и PBK равны, следовательно, Значит, SK : KB = 3 : 1.

б) Рассмотрим сечение пирамиды плоскостью SCF. Так как боковое ребро пирамиды вдвое больше ребра основания треугольник SCF — равносторонний. Пусть RT — его средняя линия параллельна плоскости основания пирамиды, как и MN, значит, они пересекаются. Назовем точку их пересечения W. Точка W — точка пересечения RT и плоскости сечения пирамиды. Значит, сечение пирамиды и плоскостьSCF пересекаются по прямой CW. Точку пересечения этой прямой с ребром SF назовем G. Таким образом требуется найти SG : GF. Точка R — середина SF, значит, R’, ее проекция на FC, — середина FO, где O — центр основания. Эта же точка является точкой пересечения AE и FC. Так как MN — средняя линия треугольника SAE, то W’ — проекция точки W на FC является серединой R’O. Таким образом, Треугольники GRW и GFC — подобны с коэффициентом Значит

Следовательно, учитывая, что R — середина SF,

а) Обозначим середины ребер SA и SE за и соответственно. Тогда MN || AE || BD. Проведем через точку C прямую, параллельную AE (она будет лежать в плоскости сечения), тогда она пересечет AB в точке Р, причем по свойствам шестиугольника AB = 2BP. Пусть теперь K точка пересечения прямой MР с SB.

По теореме Менелая для треугольника ASB и прямой MKР имеем откуда

то есть SK : KB = 3 : 1.

б) Опустим из S перпендикуляр на AE. Он упадет в середину AE — точку R’. По свойствам шестиугольника CR’ : R’F = 3 : 1. При этом отрезок MN пересекает SR’ в его середине W.

Пусть CW пересекает SF в точке G, это и есть точка пересечения плоскости сечения с ребром CF.

По теореме Менелая для треугольника FSR’ и прямой GWC имеем откуда

то есть SG : GF = 3 : 4.

Дана правильная шестиугольная пирамида SABCDEF с вершиной S.

а) Докажите, что плоскость, проходящая через середины рёбер SA и SD и вершину C, делит апофему грани ASB в отношении 2 : 1, считая от вершины S.

б) Найдите отношение, в котором плоскость, проходящая через середины рёбер SA и SD и вершину C, делит ребро SF, считая от вершины S.

а) Обозначим за M, N середины ребер SA и SD. Поскольку MN — средняя линия треугольника SAD, то поэтому точка B также лежит в данной плоскости. Поэтому с гранью ABS данная плоскость пересекается по прямой BM — медиане треугольника SAB. Она делит его медиану SQ (Q — середина AB) в отношении 2 : 1 считая от вершины.

б) Пусть Поскольку MN — средняя линия треугольника SAD, она делит отрезок SK пополам, то есть T — середина SK. Ясно, что T лежит в данной плоскости.

Рассмотрим теперь треугольник SBF. В нем проведена медиана SK и отмечена ее середина T. В данной плоскости лежит прямая BT, пересекающая SF в точке W. Осталось выяснить местоположение точки W.

Напишем теорему Менелая для треугольника FSK и прямой откуда

Можно поподробнее, откуда вы взяли, что точка В лежит в плоскости сечения?

из параллельности

На мой взгляд, условие, состоящее в том, что боковое ребро вдвое больше ребра основания, не используется при решении задачи и является лишним.

Согласны, убрали из условия это уточнение.

Склад имеет форму прямоугольного параллелепипеда, длины рёбер которого выражаются целыми числами. Этот склад заполняют контейнерами размером 1×1×3. При этом контейнеры можно располагать как угодно, но их грани должны быть параллельны граням склада.

а) Могло ли получиться так, что склад объёмом 150 невозможно полностью заполнить контейнерами?

б) Могло ли получиться так, что на складе объёмом 400 невозможно разместить 133 контейнера?

в) Какой наибольший процент объёма любого склада объёмом не менее 200 гарантированно удастся заполнить контейнерами?

а) Длина одного из рёбер параллелепипеда объёмом 150 делится на 3. Значит, если расположить все контейнеры так, чтобы их длинное ребро было параллельно этому ребру параллелепипеда, то склад будет полностью заполнен.

б) Рассмотрим склад размером 2×2×100. Контейнеры в нём могут располагаться только так, что их длинное ребро параллельно длинному ребру склада. Таким образом, любой из контейнеров целиком располагается в одном из четырёх параллелепипедов размером 1×1×100, на которые можно разбить параллелепипед размером 2×2×100. Но в каждый из этих четырёх параллелепипедов можно поместить нс более 33 контейнеров. Значит, на складе невозможно разместить более 132 контейнеров.

в) Пусть склад имеет размеры a×b×c. Покажем, что его можно заполнить контейнерами так, что останется свободное пространство объёмом a₀b₀c₀, где a₀, b₀, c₀ остатки от деления на 3 чисел a, b и c соответственно. Параллелепипед размером a×b×c можно разбить на параллелепипеды размером и Каждый из этих параллелепипедов, кроме последнего, можно полностью заполнить контейнерами, поскольку длина одного из рёбер каждого из этих параллелепипедов делится на 3. Таким образом, останется незаполненным только параллелепипед размером объём которого равен a₀b₀c₀.

Заметим, что для любых чисел а, b и с значение выражения a₀b₀c₀ не превосходит 8. Значит, склад объёмом не менее 200 всегда можно заполнить контейнерами так, чтобы объём свободного пространства был не более 8. Таким образом, можно гарантировать, что не менее 96% склада будет заполнено.

Аналогично пункту б, в склад размером 2×2×50 нельзя поместить больше 64 контейнеров. То есть в этом случае можно заполнить не более 96% склада.

Ответ: а) нет; б) да; в) 96.

Аналоги к заданию № 525383: 527255 Все

Шар проходит через вершины одной грани куба и касается сторон противоположной грани куба.

а) Докажите, что сфера касается ребер в их серединах.

б) Найдите объем шара, если ребро куба равно 1.

Нетрудно решить задачу чисто геометрически (сделайте это). Мы укажем аналитический путь.

Заметим, что сфера касается ребер в их серединах. Введем обозначения так, как показано на рисунке, введем прямоугольную систему координат с центром в вершине куба А, оси направим вдоль ребер (см. рис.), и пусть центр сферы имеет координаты (x₀, y₀, z₀), а радиус сферы равен R. Тогда уравнение сферы будет

а лежащие на сфере точки A, B, D и точка касания сферы с серединой ребра удовлетворяют соответственно уравнениям:

откуда то есть

Тогда объем шара равен

Ответ:

В правильной треугольной пирамиде с основанием известны ребра

а) Докажите, что

б) Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер и

а) Спроецируем вершину S на плоскость ABC. Получится точка O — центр правильного треугольника ABC. Значит, а тогда, по теореме о трех перпендикулярах

б) Пусть и — середины ребер и соответственно. — медиана правильного треугольника следовательно, находится по формуле Прямая проецируется на плоскость основания и прямую Поэтому проекция точки — точка — лежит на отрезке Значит, прямая является проекцией прямой следовательно, угол — искомый.

где — центр основания, значит, — средняя линия треугольника поэтому Тогда и Из прямоугольного треугольника находим:

Из прямоугольного треугольника находим:

Значит, искомый угол равен

Ответ:

В правильной треугольной пирамиде SABC с основанием ABC известны ребра SC = 17.

а) Докажите, что

б) Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер AS и BC.

а) Спроецируем вершину S на плоскость ABC. Получится точка O — центр правильного треугольника ABC. Значит, а тогда, по теореме о трех перпендикулярах

б) Пусть и — середины ребер и соответственно. — медиана правильного треугольника следовательно, находится по формуле Прямая проецируется на плоскость основания и прямую Поэтому проекция точки — точка — лежит на отрезке Значит, прямая является проекцией прямой следовательно, угол — искомый.

где — центр основания, значит, — средняя линия треугольника поэтому Тогда и Из прямоугольного треугольника находим:

Из прямоугольного треугольника находим:

Значит, искомый угол равен

Ответ:

В правильной треугольной пирамиде с основанием известны ребра

а) Докажите, что

б) Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер и

а) Спроецируем вершину S на плоскость ABC. Получится точка O — центр правильного треугольника ABC. Значит, а тогда, по теореме о трех перпендикулярах

б) Пусть и — середины ребер и соответственно. — медиана правильного треугольника следовательно, находится по формуле Прямая проецируется на плоскость основания и прямую Поэтому проекция точки — точка — лежит на отрезке Значит, прямая является проекцией прямой следовательно, угол

где — центр основания, значит, — средняя линия треугольника поэтому Тогда и Из прямоугольного треугольника находим:

Из прямоугольного треугольника находим:

Значит, искомый угол равен

Ответ:

В правильной треугольной пирамиде с основанием известны ребра

а) Докажите, что

б) Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер и

а) Спроецируем вершину S на плоскость ABC. Получится точка O — центр правильного треугольника ABC. Значит, а тогда, по теореме о трех перпендикулярах

б) Пусть и — середины ребер и соответственно. — медиана правильного треугольника следовательно, находится по формуле Прямая проецируется на плоскость основания и прямую Поэтому проекция точки — точка — лежит на отрезке Значит, прямая является проекцией прямой следовательно, угол

где — центр основания, значит, — средняя линия треугольника поэтому Тогда и Из прямоугольного треугольника находим:

Из прямоугольного треугольника находим:

Значит, искомый угол равен

Ответ:

нельзя ли этот угол найти через косинус

ведь в основании пирамиды равносторонний треугольник, если провести окружность, то АО=ОN=30:2=15 как радиусы, а так как АМ1=1/2 АО, то АМ1=АО:2=15:2=7,5

Вы, собственно какую окружность имеете в виду? И какое отношение эта окружность имеет к точке И уж точно ни при каких обстоятельствах

Зачтут ли ответ arctg 0.55?

Возможно, вы имели ввиду Да, зачтут.

Дана треугольная пирамида ABCD с вершиной D, грани которой ABD и ACD — прямоугольные треугольники, ребро AD перпендикулярно медиане основания АК и AD = AK. Сечение пирамиды плоскостью, не проходящей через середины ребер AD и ВС, является равнобочная трапеция EFGH с основаниями EF и GH, причем точка Е делит ребро BD пополам, а точка G лежит на ребре АС и AG = 3GC. Найти отношение площади трапеции EFGH к площади грани BCD.

Докажем, что ребро AD перпендикулярно основанию пирамиды. Пусть это не так, тогда заметим, что лучи АВ и АС лежат по разные стороны от АК, и поэтому один из углов DAB или DAC — тупой. Но тогда один из треугольников ABD или ACD не может быть прямоугольным, что противоречит условию. Следовательно, AD перпендикулярно ABC.

Теперь докажем, что плоскость сечения параллельна ребру BC. Рассмотрим параллельные стороны сечения, они должны быть параллельны какому-то из ребер AD, BC, CD, AB (это следует из того, что две плоскости, проходящие через параллельные прямые пересекаются по прямой, параллельной данным прямым). Если прямая EF параллельна прямой CD, то F является серединой ребра BC, а это невозможно по условию. Пусть теперь прямая EF параллельна прямой AB, тогда F является серединой ребра AD, что также невозможно. Если прямая EF параллельна прямой AD, то трапеция прямоугольная, то есть не может быть равнобедренной. Значит, основания трапеции EFGH параллельны ребру BC.

Пусть далее

1. Точка E — середина BD, прямая EF параллельна прямой BC, следовательно, F — середина DC. Пусть — проекции точек E и F на плоскость основания пирамиды. Тогда: т. к. трапеция равнобедренная, тогда и — равнобедренная трапеция. Тогда

и BAC — равнобедренный. Прямая AK — медиана равнобедренного треугольника, следовательно, прямая AK перпендикулярна прямой BC, и тогда по теореме о трех перпендикулярах прямая DK перпендикулярна прямой BC.

2. Из треугольника DAK найдем тогда площадь треугольника BDC равна

3. Имеем: EN — высота трапеции EFGH, тогда прямая перпендикулярна прямой HG и прямая параллельна прямой AK. Далее,

Найдем площадь трапеции EFGH:

4. В итоге получаем:

Ответ:

В треугольной пирамиде длины двух непересекающихся рёбер равны 12 и 4, а остальные рёбра имеют длину 7. В пирамиду вписана сфера. Найти расстояние от центра сферы до ребра длины 12.

Пусть — середины этих ребер соответственно. Тогда центр вписанной сферы лежит в бисектральной плоскости, проходящей через ребро то есть в (она перпендикудярна поэтому тетраэдр симметричен относительно нее). Аналогично центр лежит и в то есть лежит на отрезке Очевидно (поскольку лежит в плоскостях, перпендикулярных этим отрезкам). Тогда

Найдем радиус вписанной сферы. Он равен

Итак, на отрезке располагается точка на расстоянии от плоскости при этом расстояния от точек и равны и Значит, она делит этот отрезок в отношении и располагается на расстоянии от точки Это и есть ответ.

Ответ:

В пирамиде SLMN даны рёбра LM = 5, MN = 9, NL = 10. Сфера радиуса касается плоскости основания LMN и боковых рёбер пирамиды. Точки касания делят эти рёбра в равных отношениях, считая от вершины S. Найти объём пирамиды.

Рассмотрим треугольники с вершинами в центре сферы,вершине и точках касания сферы с боковыми ребрами. Они все равны по гипотенузе (общей) и катету (радиусу), поэтому у них равны и расстояния от точек касания до Из условия о равенстве отношений получаем, что боковые ребра пирамиды равны. Следовательно, ее высота падает в центр H описанной окружности основания.

Пусть это отношение было равно Продолжим луч O (O — центр сферы) и отметим точку так, чтобы Тогда перпендикуляры из на боковые ребра будут падать в то есть точка равноудалена от них. Поэтому ее проекция на плоскость — центр описанной окружности треугольника Следовательно, O лежит на Тогда

Рассмотрим треугольник SHN. Пусть тогда (поскольку O равноудалена от ON и SN, она лежит на биссектрисе угла). Тогда

Ответ:

Приведем другое решение.

Пусть сфера касается боковых ребер SL, SM, SN пирамиды в точках P, Q, T соответственно. O — центр сферы.

Тогда у пирамиды OPQT с основанием PQT боковые ребра равны как радиусы сферы. А значит, вершина O проектируется в центр описанной окружности (назовем K) около основания (действительно, прямоугольные треугольники PKO, QKO, TKO равны по гипотенузе и катету, а значит точка K равноудалена от каждой вершины основания PQT).

Но ведь тогда и, в обратную сторону, в пирамиде SPQT боковые ребра равны, раз ее вершина S спроектировалась в центр описанной окружности около основания.

А поскольку по условию точки касания сферы делят боковые ребра пирамиды в равных отношениях, считая от вершины S, то и LS = MS = NS, а также S проектируется в центр описанной окружности около треугольника LMN.

Ну и поскольку плоскости (PQT), (LMN) параллельны, то и точки S, K, O, H лежат на одной прямой.

Найдем радиус описанной окружности около основания LMN пирамиды SLMN, а так же площадь основания пирамиды.

По формуле Герона где имеем:

Тогда, пользуясь формулой нахождения радиуса описанной окружности около треугольника с площадью S и сторонами a, b, с: имеем:

Обратимся к прямоугольному треугольнику SMH. Как мы знаем, радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости, то есть OQ ꓕ SM. Тогда из равенства треугольников OMH и OMQ (по гипотенузе у катету) следует, что OM — биссектриса угла SMH.

Пусть Из треугольника OMH имеем:

Из треугольника SMH:

Как только мы найдем — мы будем знать высоту пирамиды (площадь основания мы уже знаем), тогда и объем будет найден. Итак,

Наконец, из треугольника SMH:

К диагонали куба провели перпендикуляры из середин ребер AB и AD. Найдите угол между этими перпендикулярами.

Пусть ребро куба равно О — центр куба, точки К и N — середины рёбер AD и AВ соответственно.

Заметим, что A₁N = NC = треугольник A₁NC равнобедренный, его медиана NO является высотой, поэтому NО — перпендикуляр к AС. Аналогично KO перпендикуляр к АС.

Найдём угол KON. Введем систему координат, как показано на рисунке. В этой системе координат:

Найдём угол между векторами из их скалярного произведения:

Следовательно,

Ребро куба ABCDA₁B₁C₁D₁ равно 4. Через середины ребер AB и BC параллельно прямой ВD₁ проведена плоскость.

А) Постройте сечение куба этой плоскостью.

Б) Найдите площадь полученного сечения.

а) Пусть — середины ребер соответственно. Продлим прямую до пересечения с и в точках соответственно. Очевидно

поскольку

Отметим теперь середины диагоналей граней и Прямые, соединяющие их с точками параллельны диагонали куба (как средние линии треугольников ), поэтому эти точки лежат в плоскости сечения. Соединим их с точками и Образовавшиеся точки пересечения с ребрами назовем а точку пересечения с ребром — Тогда — искомое сечение.

б) Обозначим середины отрезков за Очевидно треугольники подобны, причем откуда Тогда Значит, высота равнобедренной трапеции равна аналогично высота треугольника равна поэтому

Ответ:

Источник