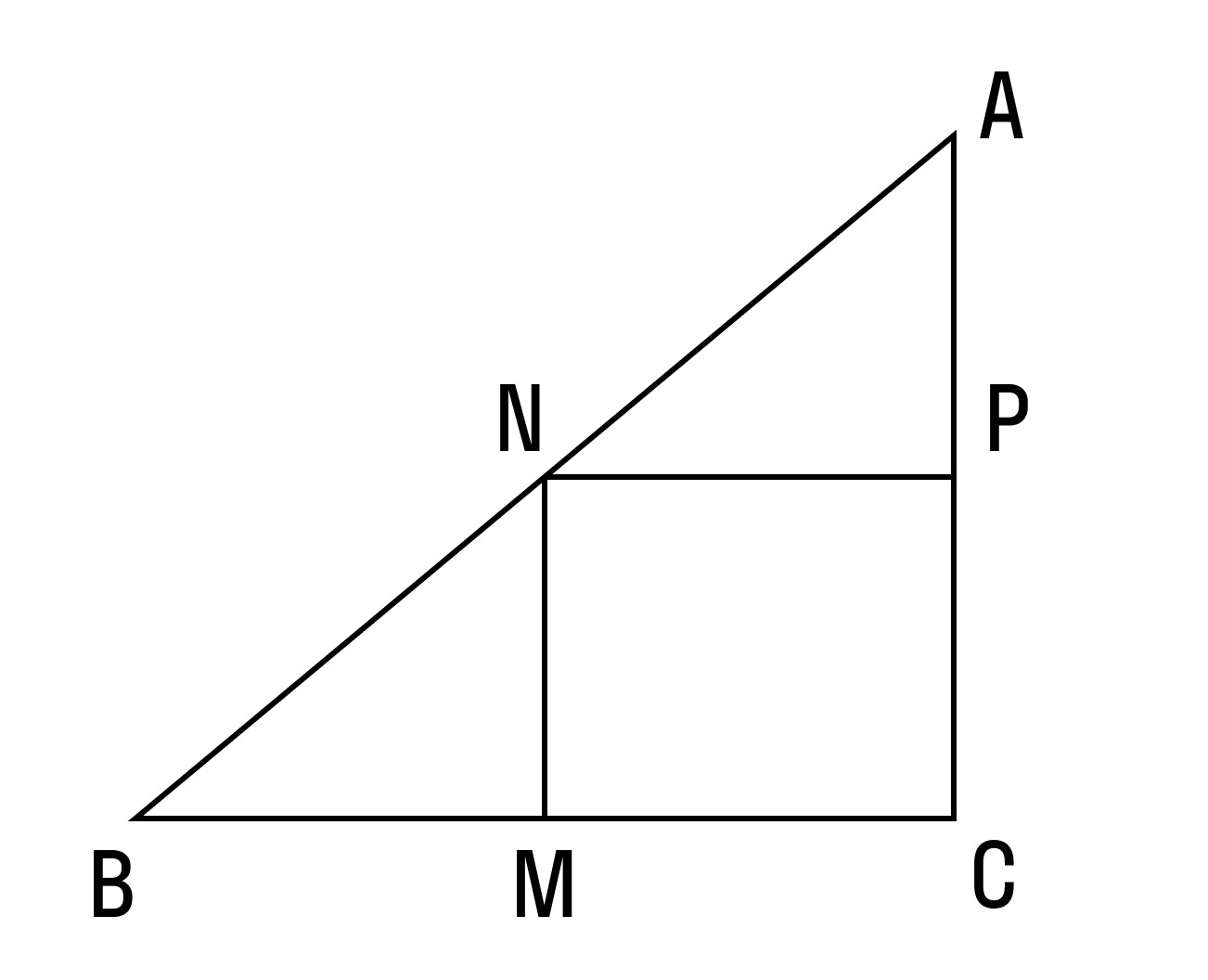
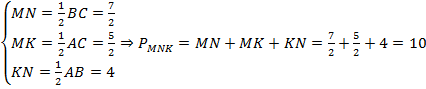Доказать что периметр треугольника образованного средними линиями данного треугольника вдвое меньше

Закрепление усвоенных умений и навыков

А класс Геометрия

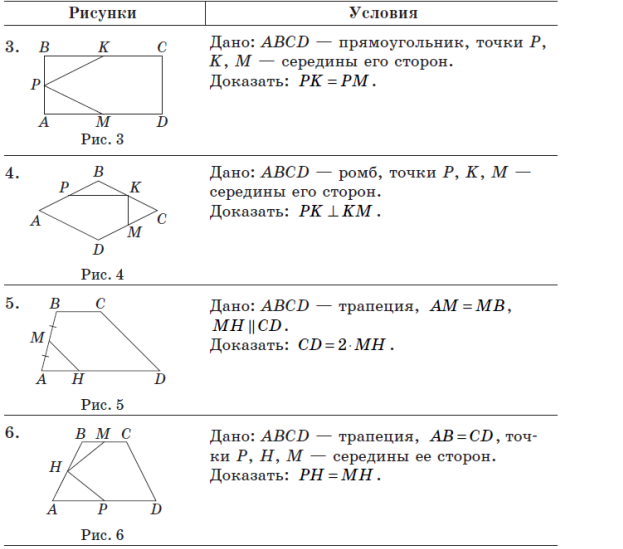
Тема урока:

Средняя линия треугольника и ее свойства.

Записать в тетради число, тему урока

Актуализация опорных знаний

Закрепление усвоенных умений и навыков

Задача 1. Докажите, что периметр одного треугольника, образованного средними линиями второго треугольника, вдвое меньшепериметра второго треугольника.

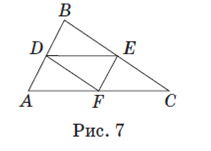
Пусть ABC (рис. 7) — данный треугольник; DE, EF, DF — его средние линии. По свойству средней линии треугольника DE= AC;

DF= BC; EF = AB. P_ΔDEF = AC+BC+AB)= P_{Δ ABC}, что и требовалось доказать.

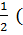
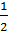
Задача 2. Периметр первого треугольника равен 76 см. Стороны второго треугольника, образованного средними линиями первого треугольника, относятся как 4:7:8. Найдите стороны первого треугольника.

Из доказанной задачи 1 следует, что периметр второго треугольника, образованного средними линиями первого треугольника, равен 76:2 =38 (см). Пусть x — коэффициент пропорциональности, тогда имеем уравнение:

Значит, стороны второго треугольника, образованного средними линиями,—

8 см, 14 см, 16 см, а стороны первого треугольника равны 16 см, 28 см и 32см.

Ответ: 16 см, 28 см, 32 см.

Задача 3. В четырехугольнике ABCD угол между диагоналями AC и BD равен 60º, AC =BD =10 см. Найдите меньшую диагональ четырехугольника, вершинами которого являются середины сторон четырехугольника ABCD.

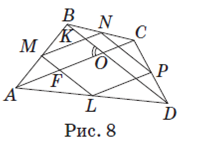
Пусть ABCD (рис. 8) — данный четырехугольник; M, N, P, L — середины сторон AB, BC, CD и AD соответственно. Как известно, четырехугольник MNPL — ромб, так как это параллелограмм с равными сторонами

(MN=NP=PL=LM=5 см= AC).

Пусть точка O — точка пересечения диагоналей AC и BD. По условию ∠BOA =60º. Четырехугольник MKOF — параллелограмм, так как MF ǁ OK и FO =MK. Значит, ∠NML =∠KOF =60º как противолежащие углы параллелограмма. Отсюда стороны ромба MN, ML и его диагональ NL образуют равносторонний треугольник MNL. Значит, NL =MN =ML =5 см. Ответ: 5 см.

Задача 4. Определите вид четырехугольника, вершины которого являются серединами сторон: а) квадрата; б) четырехугольника с взаимно перпендикулярными диагоналями.

Задача 5. В четырехугольнике последовательно соединены отрезками середины сторон. В свою очередь, в образовавшемся четырехугольнике

середины его сторон тоже последовательно соединены отрезками. Полученный таким образом четырехугольник — ромб. Докажите, что диагонали исходного четырехугольника перпендикулярны.

Источник

Как найти среднюю линию треугольника?

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие треугольника

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.

Треугольник, у которого все стороны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Свойства треугольников:

Понятие средней линии треугольника

Определение средней линии треугольника подходит для любого вида этой фигуры.

​Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.

​Основанием считается сторона, которой параллельна средняя линия.

Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.

Понятие средней линии прямоугольного треугольника

Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

Свойства средней линии треугольника

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

Свойства:

Теорема о средней линии треугольника

Теорема о средней линии треугольника звучит так:

Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:

Докажем теорему:

По условию нам дано, что MA = MB, NA = NC

Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.

(по второму признаку подобия треугольников).

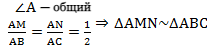
△ABC, то 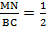Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.

Параллельность средней линии и соответствующего ей основания доказана.

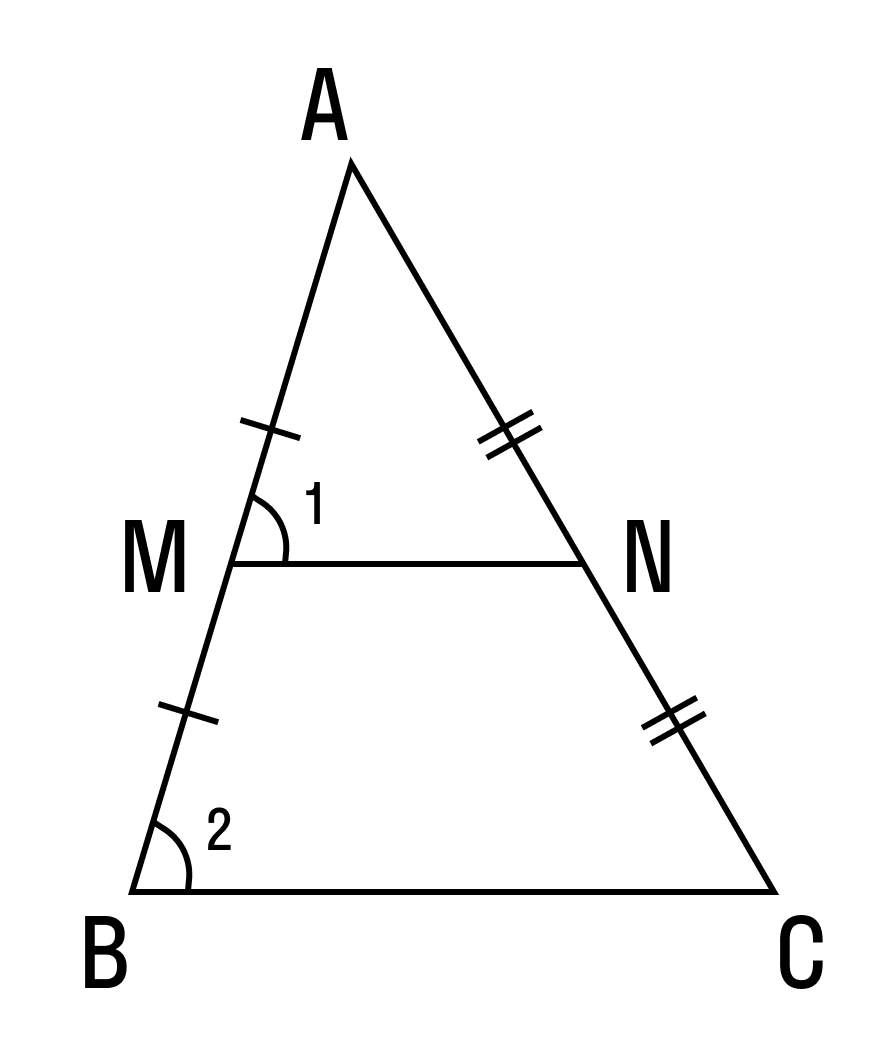
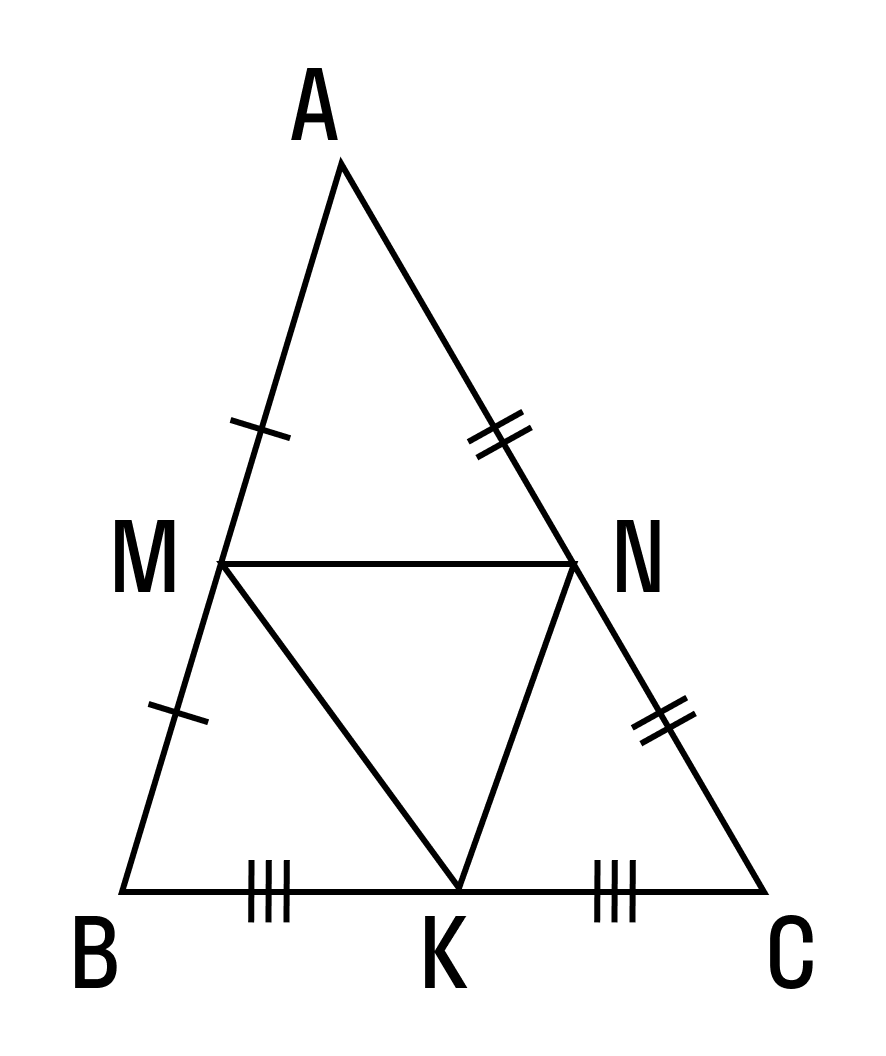
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:

Ответ: периметр треугольника ΔMNK равен 10.

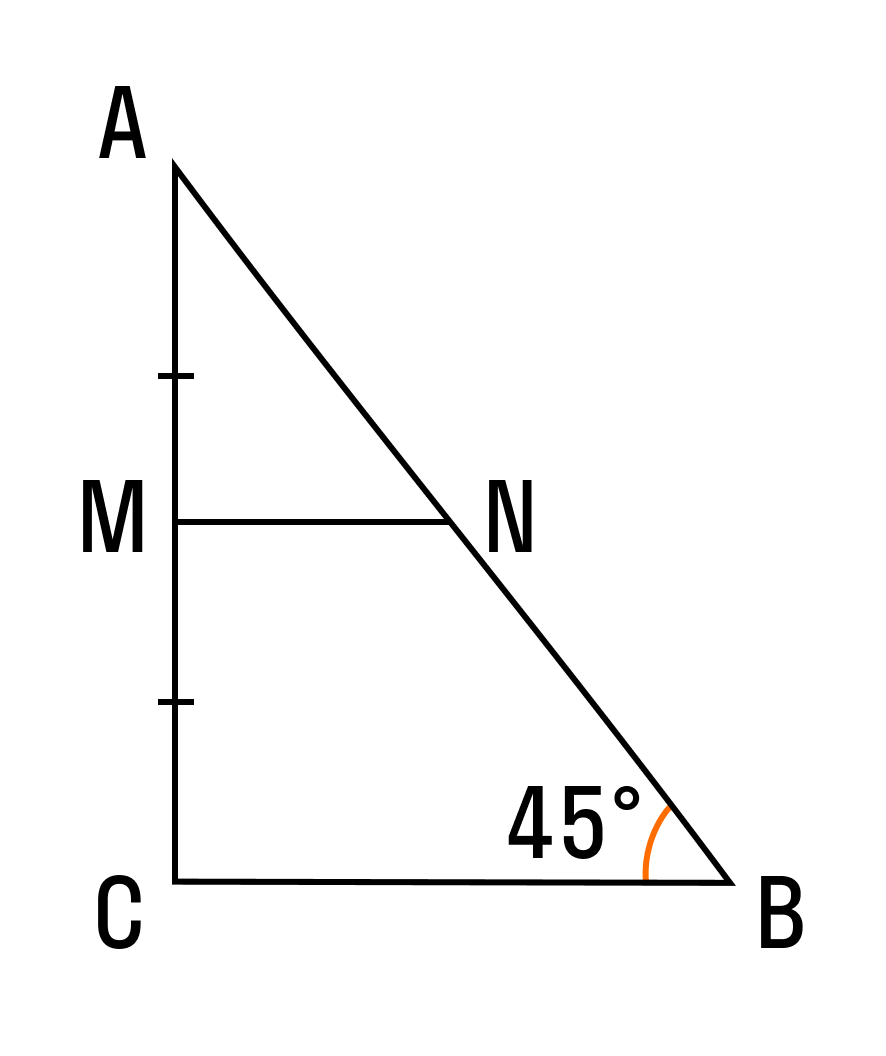
Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:

Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:

Значит, AC = 2MN = 2 × 3 = 6.

Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:

Значит, BC = 2NP = 2 × 4 = 8.

Тогда найдем площадь большого треугольника, используя формулу, указанную выше:

S = ½ × 6 × 8 = ½ × 48 = 24.

Ответ: площадь большого прямоугольного треугольника равна 24.

Источник