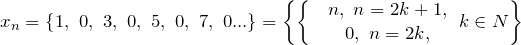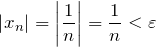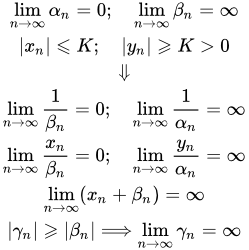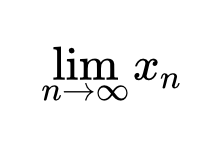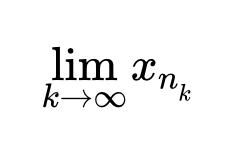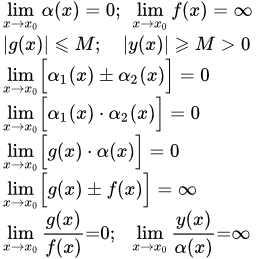Доказать что последовательность бесконечно большая

Бесконечно малые и бесконечно большие последовательности

Бесконечно большие последовательности

Следствие. Любая бесконечно большая последовательность является неограниченной.

Замечание 2. Обратное утверждение в общем случае неверно.

является неограниченной, но не является бесконечно большой. Покажем это.

Бесконечно малые последовательности

Замечание 3. Любая бесконечно малая последовательность является ограниченной, но не наоборот.

Примеры решения задач

Задание	Доказать, что последовательность 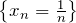является бесконечно малой.
Доказательство	Зададим произвольное положительное число и найдем такой номер 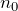элемента этой последовательности, что для всех выполняется соотношение

Что и требовалось доказать.

Источник

Свойства бесконечно больших последовательностей

Формулировки свойств

Связь между бесконечно большой и бесконечно малой последовательностью

Сумма бесконечно большой и ограниченной последовательности

Произведение бесконечно большой и ограниченной снизу последовательности

Частное ограниченной и бесконечно большой последовательности

Если последовательность < β_n > бесконечно большая, с неравными нулю членами, а последовательность < x_n > ограничена, то
.
Доказательство ⇓

Частное ограниченной снизу и бесконечно малой последовательностью

Если абсолютные значения элементов последовательности < y_n > ограничены снизу положительным числом ( | y_n | ≥ K > 0 ), а < α_n > – бесконечно малая с неравными нулю членами, то
.
Доказательство ⇓

Свойство неравенств бесконечно больших последовательностей

Это свойство имеет два частных случая, которые доказываются аналогичным способом.

Арифметические свойства бесконечно больших и бесконечно малых последовательностей

Приведенные выше свойства выполняются, если последовательность ограничена, а последовательность абсолютных членов ограничена снизу положительным числом. При этом эти последовательности не обязательно должны иметь конечный предел, а могут расходиться. Однако, эти последовательности будут обладать указанными свойствами, если они имеют соответствующие пределы. Это позволяет сформулировать арифметические свойства бесконечно больших и бесконечно малых последовательностей.

Доказательство свойств

Связь между бесконечно большой и бесконечно малой последовательностью

Первая часть свойства доказана.

Умножим первое неравенство (1.2) на положительное число :
.
Тогда вместо (1.2) имеем:
.
Подставим :
.

Сумма бесконечно большой и ограниченной последовательности

Произведение бесконечно большой и ограниченной снизу последовательности

Частное ограниченной и бесконечно большой последовательности

Все свойства ⇑ Если последовательность < β_n > бесконечно большая, с неравными нулю членами, а последовательность < x_n > ограничена, то
.

Поскольку последовательность является бесконечно большой, то, согласно свойству 1, последовательность с членами является бесконечно малой. Но произведение ограниченной последовательности на бесконечно малую является бесконечно малой последовательностью. См. «Произведение ограниченной последовательности на бесконечно малую». Поэтому
.

Частное ограниченной снизу и бесконечно малой последовательностью

Все свойства ⇑ Если абсолютные значения элементов последовательности < y_n > ограничены снизу положительным числом ( | y_n | ≥ K > 0 ), а < α_n > – бесконечно малая с неравными нулю членами, то
.

Свойство неравенств бесконечно больших последовательностей

Источник

Предел последовательности – основные теоремы и свойства

Определение последовательности

Более подробно см. страницу Определение числовой последовательности >>>.
Далее мы будем считать, что элементами последовательности являются действительные числа.

Верхнюю грань также называют точной верхней границей, а нижнюю грань – точной нижней границей. Понятия верхней и нижней граней справедливы не только к последовательностям, но и к любым множествам действительных чисел.

Определение предела последовательности

С помощью логических символов существования и всеобщности определение предела можно записать следующим образом:
.

Свойства конечных пределов последовательностей

Основные свойства

Точка a является пределом последовательности тогда и только тогда, когда за пределами любой окрестности этой точки находится конечное число элементов последовательности или пустое множество.

Теорема единственности предела числовой последовательности. Если последовательность имеет предел, то он единственный.

Если последовательность имеет конечный предел, то она ограничена.

Если у последовательности добавить, отбросить или изменить первые m элементов, то это не повлияет на ее сходимость.

Арифметические действия с пределами

Свойства, связанные с неравенствами

Бесконечно большая и бесконечно малая последовательности

Бесконечно малая последовательность

Сумма и разность конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.

Произведение ограниченной последовательности на бесконечно малую является бесконечно малой последовательностью.

Произведение конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.

Доказательства свойств бесконечно малых последовательностей приведены на странице
Бесконечно малые последовательности – определение и свойства >>>.

Бесконечно большая последовательность

Если последовательность бесконечно большая, а последовательность ограничена, то
.

Если абсолютные значения элементов последовательности ограничены снизу положительным числом ( ), а – бесконечно малая с неравными нулю элементами, то
.

Более подробно определение бесконечно большой последовательности с примерами приводится на странице
Определение бесконечно большой последовательности >>>.
Доказательства свойств бесконечно больших последовательностей приведены на странице
Свойства бесконечно больших последовательностей >>>.

Критерии сходимости последовательностей

Монотонные последовательности

Аналогичными неравенствами определяются другие монотонные последовательности.

Строго убывающая последовательность:
.
Неубывающая последовательность:
.
Невозрастающая последовательность:
.

Отсюда следует, что строго возрастающая последовательность также является неубывающей. Строго убывающая последовательность также является невозрастающей.

Монотонная последовательность – это неубывающая или невозрастающая последовательность.

Теорема Вейерштрасса. Для того чтобы неубывающая (невозрастающая) последовательность имела конечный предел, необходимо и достаточно, чтобы она была ограниченной сверху (снизу ). Здесь M – некоторое число.

Поскольку любая неубывающая (невозрастающая) последовательность ограничена снизу (сверху), то теорему Вейерштрасса можно перефразировать следующим образом:

Монотонная неограниченная последовательность имеет бесконечный предел, равный для неубывающей и для невозрастающей последовательности.

Критерий Коши сходимости последовательности

Фундаментальная последовательность – это последовательность, удовлетворяющая условию Коши.

Критерий Коши сходимости последовательности. Для того, чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она удовлетворяла условию Коши.

Доказательство критерия сходимости Коши приведено на странице
Критерий Коши сходимости последовательности >>>.

Подпоследовательности

Доказательство теоремы Больцано – Вейерштрасса приведено на странице
Теорема Больцано – Вейерштрасса >>>.

Определения, теоремы и свойства подпоследовательностей и частичных пределов рассмотрены на странице
Подпоследовательности и частичные пределы после­довательностей>>>.

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
В.А. Зорич. Математический анализ. Часть 1. Москва, 1997.
В.А. Ильин, Э.Г. Позняк. Основы математического анализа. Часть 1. Москва, 2005.

Источник

Подпоследовательности и частичные пределы последовательностей

Определение подпоследовательности

Свойства подпоследовательностей

Свойство 3 является следствием свойств 1 и 2.

Частичный предел последовательности

Произвольная последовательность может иметь конечное или бесконечное число частичных пределов ⇑.

5. Свойство частичного предела последовательности
Точка является частичным пределом последовательности тогда и только тогда, когда в любой окрестности точки a содержится бесконечное число членов последовательности.
Доказательство ⇓

Верхний и нижний частичные пределы

Рассмотрим множество частичных пределов последовательности. Эта теорема утверждает, что верхняя и нижняя грани этого множества являются ее элементами. То есть множество частичных пределов последовательности замкнуто, оно содержит свою границу. Для произвольного множества это может не выполняться. Например, для открытого интервала не существует наибольшего и наименьшего элемента, поскольку и верхняя грань b и нижняя a не принадлежит этому множеству.

Если последовательность не ограничена сверху, то ее верхний частичный предел равен плюс бесконечности:
.
Соответственно, если последовательность не ограничена снизу, то
.

Если последовательность ограничена, то ее верхний и нижний частичные пределы конечны.

8. Теорема о неравенстве между верхним и нижним частичными пределами
Верхний и нижний частичные пределы последовательности удовлетворяют неравенству:
.
Частичные пределы равны друг другу тогда и только тогда, когда существует предел последовательности:
.
Доказательство ⇓

9. Связь верхних и нижних пределов между последовательностями n> и <–x_n>.
Имеет место очевидное равенство:
.

10. Свойства верхних и нижних пределов суммы последовательностей
Верхний и нижний частичные пределы от суммы последовательностей удовлетворяют следующим неравенствам:
;
,
где последовательности и ограничены.
Доказательство ⇓

11. Свойство верхних пределов произведения последовательностей
Пусть последовательность сходится к конечному положительному числу:
.
И пусть – любая последовательность. Тогда
.
Отсюда
.
Доказательство ⇓

Применяя равенство
,
можно получить другие подобные соотношения.

Доказательство свойств и теорем

Далее перечислены определения и свойства, которые мы будем использовать при доказательстве свойств подпоследовательностей.

1. Свойство подпоследовательностей сходящейся последовательности

2. Свойство последовательности, все подпоследовательности которой сходятся к одному числу

5. Свойство частичного предела последовательности

Все свойства ⇑ Точка является частичным пределом последовательности тогда и только тогда, когда в любой окрестности точки a содержится бесконечное число членов последовательности.

Возьмем произвольную окрестность точки a : ⇑. В качестве первого члена подпоследовательности возьмем любой член последовательности, принадлежащий этой окрестности.

6. Теорема о существовании верхнего и нижнего частичных пределов

В этом случае точка является верхним частичным пределом последовательности.

Пусть последовательность ограничена сверху и при этом любой отрезок содержит только конечное число членов последовательности.

Поскольку мы выбирали самые правые отрезки с бесконечным числом членов, то точка c является верхним частичным пределом последовательности.

7. Свойство верхнего и нижнего частичных пределов

8. Теорема о неравенстве между верхним и нижним частичными пределами

Все свойства ⇑ Верхний и нижний частичные пределы последовательности удовлетворяют неравенству:
.
Частичные пределы равны друг другу тогда и только тогда, когда существует предел последовательности:
.

10. Свойства верхних и нижних пределов суммы последовательностей

Все свойства ⇑ Верхний и нижний частичные пределы от суммы последовательностей удовлетворяют следующим неравенствам:
;
,
где последовательности и ограничены.

Докажем второе неравенство:
.
Умножим первое неравенство на – 1 :
.
Применим свойство 8 ⇑:
.

11. Свойство верхних пределов произведения последовательностей

Все свойства ⇑ Пусть последовательность сходится к конечному положительному числу:
.
И пусть – любая последовательность. Тогда
.
Отсюда
.

Из (10.1) и (10.2) следует, что
.
Свойство доказано.

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Бесконечно малые и бесконечно большие функции

Определение бесконечно малой и бесконечно большой функции

Свойства бесконечно малых функций

Свойство суммы, разности и произведения бесконечно малых функций

Теорема о произведении ограниченной функции на бесконечно малую

Свойство о представлении функции в виде суммы постоянной и бесконечно малой функции

Свойства бесконечно больших функций

Теорема о сумме ограниченной функции и бесконечно большой

Теорема о произведении ограниченной снизу функции на бесконечно большую

Теорема о частном от деления ограниченной функции на бесконечно большую

Теорема о частном от деления ограниченной снизу функции на бесконечно малую

Свойство неравенств бесконечно больших функций

Это свойство имеет два частных случая.

Связь между бесконечно большими и бесконечно малыми функциями

Из двух предыдущих свойств вытекает связь между бесконечно большими и бесконечно малыми функциями.

Дополнительные формулы, связывающие символы бесконечности, можно найти на странице
«Бесконечно удаленные точки и их свойства».

Арифметические свойства бесконечно больших и бесконечно малых функций

Приведенные выше свойства выполняются, если функция ограничена, а функция ограничена снизу по абсолютной величине положительным числом. При этом эти функции не обязательно должны иметь конечный предел, а могут расходиться. Однако, эти функции будут обладать указанными свойствами, если они имеют соответствующие пределы. Это позволяет сформулировать арифметические свойства бесконечно больших и бесконечно малых функций.

Доказательство свойств и теорем

Теорема о произведении ограниченной функции на бесконечно малую

Для доказательства этой теоремы, мы воспользуемся определением предела функции по Гейне. А также используем свойство бесконечно малых последовательностей, согласно которому произведение ограниченной последовательности на бесконечно малую является бесконечно малой последовательностью.

Воспользуемся тем, что произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность:
.
Тогда, согласно определению предела последовательности по Гейне,
.

Свойство о представлении функции в виде суммы постоянной и бесконечно малой функции

Теорема о сумме ограниченной функции и бесконечно большой

Для доказательства теоремы, мы воспользуемся определением предела функции по Гейне. Также используем свойство бесконечно больших последовательностей, согласно которому сумма или разность ограниченной последовательности и бесконечно большой является бесконечно большой последовательностью.

Поскольку сумма или разность ограниченной последовательности и бесконечно большой является бесконечно большой последовательностью, то
.
Тогда, согласно определению предела последовательности по Гейне,
.

Теорема о произведении ограниченной снизу функции на бесконечно большую

Для доказательства этого свойства, мы воспользуемся определением предела функции по Гейне. Также используем свойство бесконечно больших последовательностей, согласно которому произведение бесконечно большой и ограниченной снизу последовательности является бесконечно большой последовательностью.

Поскольку произведение бесконечно большой и ограниченной снизу последовательности является бесконечно большой последовательностью, то
.
Согласно определению предела последовательности по Гейне,
.

Теорема о частном от деления ограниченной функции на бесконечно большую

Для доказательства, мы воспользуемся определением предела функции по Гейне. Также используем свойство бесконечно больших последовательностей, согласно которому частное от деления ограниченной последовательности на бесконечно большую является бесконечно малой последовательностью.

Поскольку частное от деления ограниченной последовательности на бесконечно большую является бесконечно малой последовательностью, то
.
Тогда, согласно определению предела последовательности по Гейне,
.

Теорема о частном от деления ограниченной снизу функции на бесконечно малую

Для доказательства этого свойства, мы воспользуемся определением предела функции по Гейне. Также используем свойство бесконечно больших последовательностей, согласно которому частное от деления ограниченной снизу последовательности на бесконечно малую является бесконечно большой последовательностью.

Поскольку частное от деления ограниченной снизу последовательности на бесконечно малую является бесконечно большой последовательностью, то
.
Согласно определению предела последовательности по Гейне,
.

Свойство неравенств бесконечно больших функций

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.

Источник