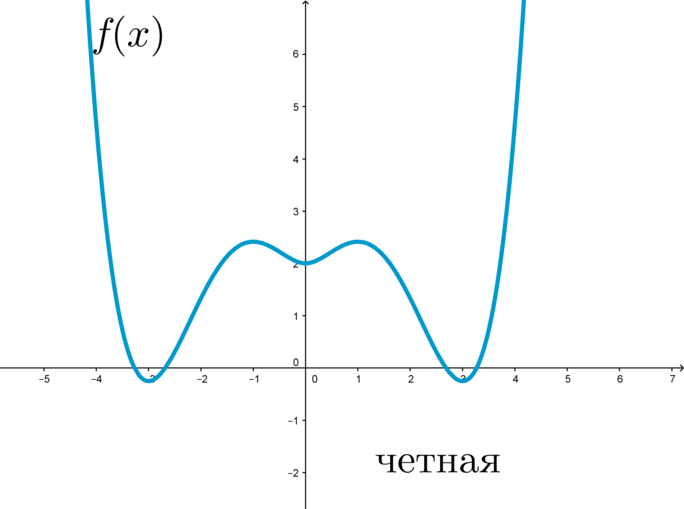
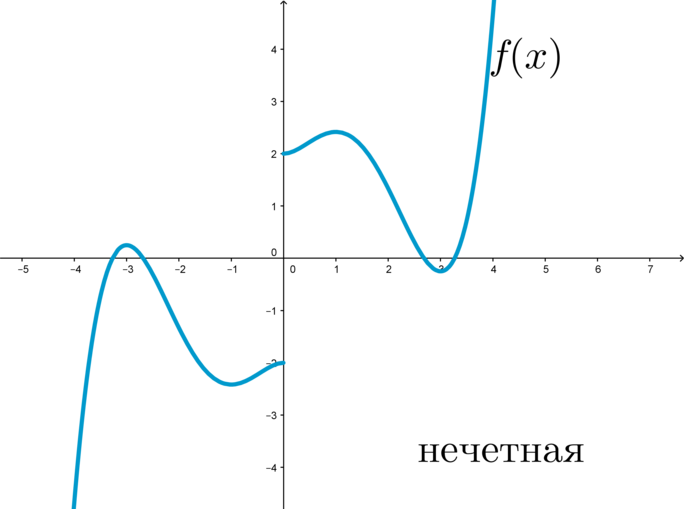
Доказать что произведение и частное двух нечетных функций являются четными

Исследовательская работа по теме: «Четность произведения двух функций»

Муниципальное образовательное учреждение

средняя общеобразовательная школа №129

Советского района Волгограда

Исследовательская работа по теме:

«Четность произведения двух функций»

обучающиеся 8 «Б» класса

Иванас Ирина Анатольевна,

Глава 1. Теоретическая подготовка и сбор материала исследования. 5

Сбор первичного фонда информации. 5

Классификация фонда. 5

Составление модели для исследования. 6

Сбор дополнительного фонда для того, чтобы можно было

исследовать все виды моделей. 6

Глава 2. Исследование собранного материала. 7

2.1. Исследование полученных моделей на четность

(по выбранному вопросу). 7

Глава 3. Гипотеза и ее проверка на практических примерах. 8

3.1. Формулировка гипотезы. 8

3.2. Проверка гипотезы на дополнительном фонде. 8

Глава 4. Обобщенная формулировка гипотезы и её теоретическое обоснование. 9

4.1. Формулировка гипотезы в виде теорем (если…, то…). 9

4.2. Доказательство теоремы в общем виде. 9

Список литературы 12

Проблема. Четность произведения двух функций.

изучение алгоритма определения четности произведения двух функций;

содействие углублению теоретического материала;

развитие познавательного интереса, расширение представления о свойствах произведения двух функций;

развитие умения осуществлять самостоятельный поиск информации, анализировать и обобщать её.

расширить знания программного материала о четности функции;

продолжить формирование умения исследовать функцию на четность с помощью определения;

формировать культуру построения графиков функций, культуру формулирования новой гипотезы и её доказательства;

развивать способность к исследовательской и проектной деятельности;

повысить информационную и коммуникативную компетентность.

расширение знаний о четности функции, четности произведения двух функций;

развитие средствами составления гипотез и их доказательства своих индивидуальных способностей и своего саморазвития;

умение использовать новую информацию и дополнительную литературу, выполнять анализ полученного материала и синтезировать его в доказательстве гипотезы.

Объектная область : математика.

Объект исследования: функции.

Предмет исследования : четность функции.

метод визуализации данных.

Новизна и практическое значение:

Изучая свойства элементарных функций (линейная, квадратичная, степень с натуральным показателем, обратная пропорциональность, модуль), мы узнали, как исследовать функцию на четность по определению. Изучаемые в школьной программе функции были исследованы нами на четность. В данной работе с помощью теоретического материала и графиков функций исследована четность произведения двух функций, что способствует углублению знаний и расширению кругозора.

Глава 1. Теоретическая подготовка и сбор материала исследования.

Изучая теоретический материал по теме «Функции и их свойства мы

познакомились со свойством четности.

По определению, которое мы нашли в дополнительной литературе,

четной называется функция f(x), обладающая следующими свойствами:

1). Область определения функции (D(f)) симметрична относительно начала отсчета;

Сбор первичного фонда информации.

Из собственного опыта мы собрали копилку конкретных примеров функций, известных из курса алгебры:
y=5x; y=-7x+5; y=x 2 ; y=x 3 ; y=x 4 ; y=x 5 ; y=|x|; y=3/x; y=5; y=x; y=5x 2 +2x-3

На этом этапе мы провели классификацию собранного фонда функций по четности.

Составление модели для исследования.

Для четности произведения двух функций, четность которых известна, возможны варианты:

Ч Ч;

Ч Н;

Н Н.

Сбор дополнительного фонда для того, чтобы можно было исследовать все виды моделей.

у=5х x 3

у= х 5 3/x

у=х x 3

Глава 2. Исследование собранного материала.

2.1. Исследование полученных моделей на четность (по выбранному вопросу).

2). z (- x ) = (- x ) 2 (- x ) 4 =(- x ) 6 = x 6 = z ( x )

2). f (- x ) = (- x ) (- x ) 3 =(- x ) 4 = x 4 = f ( x )

Глава 3. Гипотеза и ее проверка на практических примерах.

3.1. Формулировка гипотезы.

В первом случае: Ч Ч=Ч (произведение двух четных функций есть четная функция).

Во втором случае: Ч Н=Н (произведение четной функции на нечетную функцию есть нечетная функция).

В третьем случае: Н Н=Ч (произведение двух нечетных функций есть четная функция).

3.2. Проверка гипотезы на дополнительном фонде.

2). у(х)=|x| 3/x

2). у(-x) =|-x| 3/(-x)=-|x| 3/x=- у(x)

3). у(х)= х 5 3/x

2). у(-x) =(-x) 5 3/(-x) =x 5 3/x= у(x)

Глава 4. Обобщенная формулировка гипотезы и её теоретическое обоснование.

4.1. Формулировка гипотезы в виде теорем (если…, то…).

1). Если перемножить две четные функции, то в результате получится четная функция.

2). Если перемножить четную и нечетную функции, то в результате получится нечетная функция.

3). Если перемножить две нечетные функции, то в результате получится четная функция.

4.2. Доказательство теоремы в общем виде.

1). Если перемножить две четные функции, то в результате получится четная функция.

2). Если перемножить четную и нечетную функции, то в результате получится нечетная функция.

3). Если перемножить две нечетные функции, то в результате получится четная функция.

Изучив теоретический материал, рассмотрев свойство четности элементарных функций, мы исследовали четность произведения двух функций, четность которых была нам уже известна. Работая над этой темой мы выяснили, что произведение двух четных функций и двух нечетных функций есть четная функция, а произведение четной функции и нечетной функции есть нечетная функция.

При помощи определения четности функции нам удалось провести исследование частных примеров, затем проверить и доказать гипотезу четности и нечетности произведения двух функций.

Изучение данной проблемы помогло нам выбрать дальнейший путь исследований.

Нами были определены следующие направления работы:

увеличить фонд за счет добавления более сложных функций. Здесь можно доказать теорему о том, что произведение любого количества четных функций есть функция четная (Ч Ч Ч … Ч=Ч);

рассмотреть частные случаи (отыскание возможных следствий из доказанной теоремы);

составить и проверить обратные утверждения.

Полученные знания и умения сбора и анализа материала, составления гипотезы и доказательства её помогут нам провести исследование по выбранному направлению.

Источник

Четные и нечетные функции

График четной функции симметричен относительно оси \(y\) :

График нечетной функции симметричен относительно начала координат:

\(\blacktriangleright\) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.

\(\blacktriangleright\) Некоторые свойства:

1) Произведение и частное двух функций одинаковой четности — четная функция.

2) Произведение и частное двух функций разной четности — нечетная функция.

3) Сумма и разность четных функций — четная функция.

4) Сумма и разность нечетных функций — нечетная функция.

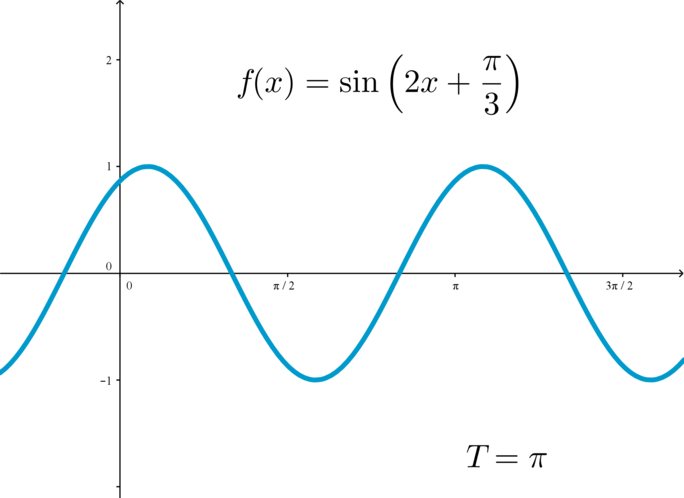
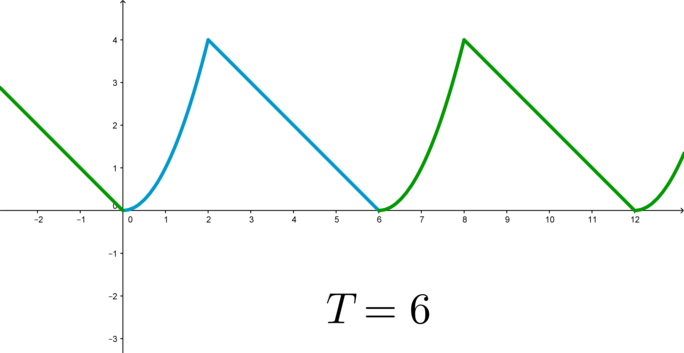
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной \(T\) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:

При каких значениях параметра \(a\) уравнение

имеет единственное решение?

\[2\cdot 0+a\mathrm\,(\cos 0)+a^2=0 \quad \Rightarrow \quad a^2+a\mathrm\,1=0 \quad \Rightarrow \quad \left[ \begin\begin &a=0\\ &a=-\mathrm\,1 \end \end\right.\]

симметричен относительно начала координат.

Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)

\(\dfrac n2, n\in\mathbb\)

(Задача от подписчиков)

имеет хотя бы один корень.

(Задача от подписчиков)

имеет шесть различных решений.

Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.

1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \[D=a^2-16a+52>0\quad\Leftrightarrow\quad a\in (-\infty;8-2\sqrt3)\cup(8+2\sqrt3;+\infty)\]

2) Также нужно, чтобы оба корня были положительными (так как \(t>0\) ). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно: \[\begin 12-a>0\\-(a-10)>0\end\quad\Leftrightarrow\quad a

Источник

Доказать что произведение и частное двух нечетных функций являются четными

ФУНКЦИИ И ПРЕДЕЛЫ IX

§ 206. Четные и нечетные функции

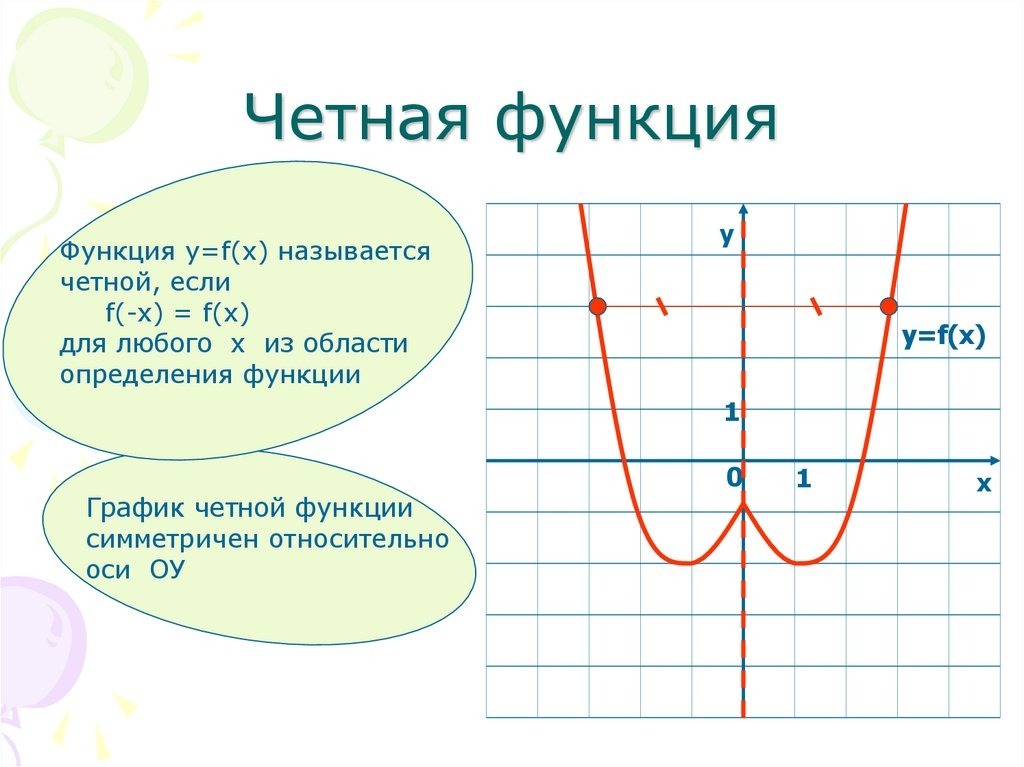
Функция у = f (х) называется четной, если при всех значениях х из области определения этой функции

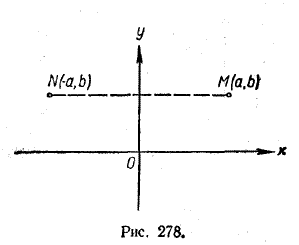
Пусть точка М с координатами (а, b) принадлежит графику четной функции у = f (х). Тогда b = f (а). Так как функция f (х) четна, то и f (— a)= f (а)= b. Но это означает, что наряду с точкой М (а, b) графику функции у = f (х) должна принадлежать и точка N с координатами (— а, b). Эти две точки симметричны друг другу относительно оси у (рис. 278).

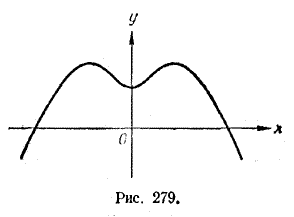
Таким образом, какую бы точку графика четной функции мы ни взяли, на нем обязательно найдется точка, симметричная первой относительно оси у. Вот почему график четной функции представляет собой линию, симметричную относительно оси ординат (один из таких графиков показан на рис. 279).

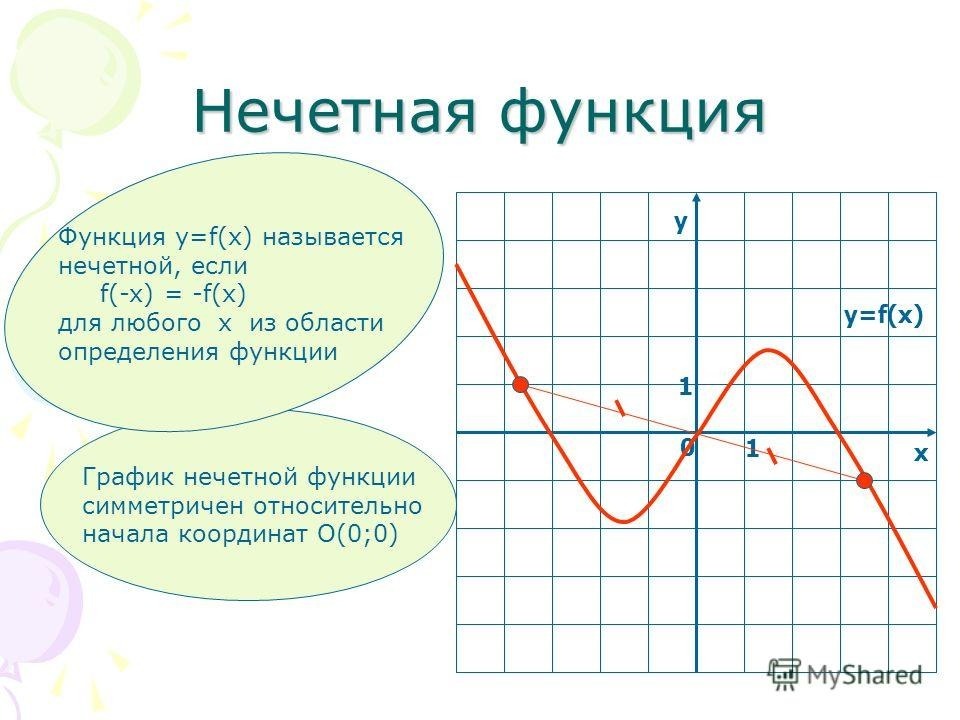
Функция у = f (x) называется нечетной, если при всех значениях х из области определения этой функции

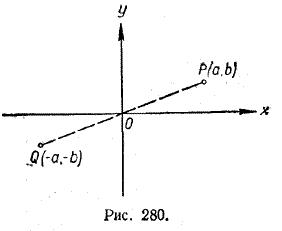
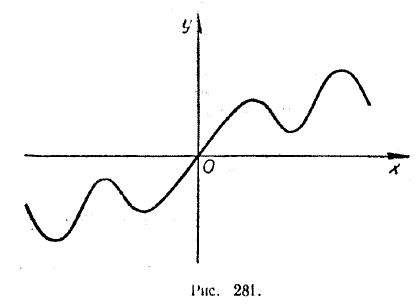
Таким образом, какую бы точку графика нечетной функции мы ни взяли, на нем обязательно найдется другая точка, симметричная первой относительно начала координат. Вот почему график любой нечетной функции симметричен относительно начала координат (см., например, рис. 281).

Кроме того, говорить о том, что функция у = f ( х) четна или нечетна, можно лишь в том случае, когда область определения этой функции является симметричной относительно начала координат. Это означает, что если функция определена при х = а, то она должна быть определена и при х = — а. В противном случае сравнивать выражения f (х) и f (— х) не имеет смысла. Например, функция у = lg х определена только для положительных значений аргумента. Поэтому одно из выражений lg х и lg (— х) наверняка не имеет смысла. Следовательно, говорить о том, является ли логарифмическая функция четной или нечетной, также не имеет смысла.

1605. (У с т н о.) Среди данных функций указать четные и нечетные:

1606. Какие из данных функций являются четными и какие нечетными:

1607. Доказать, что сумма, разность, произведение и частное двух четных функций являются четными функциями.

1608. Доказать, что произведение и частное двух нечетных функций представляют собой четные функции.

1609. Может ли функция быть одновременно и четной и нечетной?

1610*. Что вы можете сказать о четности функции f ( х), если известно, что функция | f ( х) | : а) четна; б) нечетна?

1611. Может ли монотонная на всей числовой прямой функция быть: а) четной; б) нечетной?

1612. Как достроить график четной функции у = f ( х), еели он задан только при х > 0?

Источник

Понятие четной и нечетной функции

Понятие четности и нечетности функции

Главное условие при исследовании функции на четность/нечетность — это симметричность области определения относительно 0. Если она не симметрична, то функция не является ни четной, ни нечетной, и дальнейшее исследование производить не нужно. Например, \(D(y)\in(-\infty;+\infty)\) симметрична относительно 0, а \(D(y):x\in(-5;9)\) — нет.

Четная функция

Функцию \(f(x)\) называют четной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=f(x).\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

График четной функции симметричен относительно оси Ох.

Нечетная функция

Функцию \(f(x)\) называют нечетной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=-f(x).\)

График нечетной функции симметричен относительно начала координат (точки (0;0)).

Произведение четной и нечетной функции

Произведение четной и нечетной функций есть нечетная функция.

Пусть \(f(x)\) — четная функция, а \(g(x)\) — нечетная. Тогда \(f(x)=f(-x), а g(-x)=-g(x).\)

Исследование функций в примерах

Доказать, что функция \(y=x^2\) четная.

1. Найдем область определения: \(D(y):x\in(-\infty;+\infty)\) — симметрична относительно 0.

Исследовать на четность и нечетность функцию \(f(x)=8x^3-7x.\)

1. Найдем область определения: \(D(f):x\in(-\infty;+\infty)\) — симметрична относительно 0.

Исследовать на четность и нечетность функции \(f_1(x)=\frac\) и \(f_2(x)=\frac4\)

Рассмотрим первую функцию:

1. Найдем область определения: x — любое число, кроме 1. Она не симметрична относительно 0, значит \( f_1(x)\) относится к функциям общего вида, то есть не является ни четной ни нечетной.

Рассмотрим вторую функцию:

Источник

Конспект урока по теме «Исследование функций на чётность и нечётность»

Учитель математики высшей категории: Петухова Ольга Владимировна

Тема урока: Исследование функций на чётность и нечётность. 10 класс

Тип урока: Комбинированный урок (с элементами проектной деятельности).

Предметная цель: организация деятельности учащихся по воспроизведению, осмыслению, обобщению знаний и овладению элементами проектной деятельности.

Закрепить понятия чётной и нечётной функции. Сформулировать правила, способствующие доказательству чётности и нечётности функции. Научить применять правила для определения чётности и нечётности функции.

Развивать познавательные навыки у учащихся, умения самостоятельно конструировать свои знания, анализировать, обобщать, доказывать, делать выводы.

Воспитывать у учащихся самостоятельность, личностную заинтересованность в приобретаемых знаниях, культуру поведения.

Методы обучения: Словесный, наглядный, элементы «метода проектов» и частично-поискового метода.

Оборудование: презентация «Исследование функций на чётность и нечётность», раздаточный материал в форме обобщающих таблиц, «Алгебра и начала анализа» учебник для 10-11 классов под ред. А.Н. Колмогорова, дополнительный справочный материал.

Форма учебного занятия – урок с элементами исследования.

1-й уровень: знать понятия «чётная функция» и «нечётная функция», уметь доказывать чётность (нечётность) функции, используя определения чётной и нечётной функций.

2-й уровень: знать понятия «чётная функция» и «нечётная функция», уметь доказывать чётность (нечётность) функции, используя определения чётной и нечётной функций; уметь обобщать и делать вывод (формулировать правила).

3-й уровень: знать понятия «чётная функция» и «нечётная функция», уметь доказывать чётность (нечётность) функции, используя определения чётной и нечётной функций; уметь обобщать и делать вывод (формулировать правила); уметь применять правила для доказательства чётности (нечётности) функции и приводить примеры чётных (нечётных) функций применительно данному правилу.

Включить презентацию. Разделить класс на 3 группы, раздать печатный материал.

I . Организационное начало урока (2 мин.).

Добрый день! Я рада вас видеть. На уроке у нас присутствуют гости. Давайте поприветствуем их поклоном головы, и посмотрите на меня. На уроке нам потребуется: учебник, ручка, раздаточный материал и хорошее настроение для получения желаемого результата от урока.

II. Вместе с учителем в ходе беседы формулируют тему урока, ставят цели достижения учебной задачи, формулируют гипотезы (8 мин.).

На экране представлены чётные и нечётные функции.

Задание: докажите, что функция является чётной (нечётной).

Учащиеся читают функцию и объясняют, почему она является чётной или нечётной (используют определение).

Учитель: а если функция является суммой, произведением или отношением двух и более чётных или нечётных функций или представляет собой сочетание нескольких чётных и нечётных функций, то есть достаточно сложная функция. Как быстро доказать чётная функция или нечётная? Чтобы ответить на эти вопросы проведём исследование различных функций и сформулируем правила, которые позволят нам сразу определять чётная функция или нечётная.

Таким образом, тема урока «Исследование функций на чётность и нечётность» (слайд 2)

Учащиеся: Выдвигают несколько гипотез (устно):

-сумма двух чётных функций – _________;

-сумма двух нечётных функций – __________;

III . Исследование функций на чётность (нечётность). (6 мин.)

1 группа исследует чётные функции; 2 группа исследует нечётные функции; 3 группа исследует сочетания чётной и нечётной функций. Каждой группе предложено некоторое количество функций, которые они должны исследовать, сделать вывод и сформулировать правило (Приложение 1). Заполняют свою часть обобщающей таблицы (Приложение 2).

IV . Представление результатов. (6 мин.)

Заполняют обобщающую таблицу на доске с пояснениями. Начинают со слов: в результате исследования мы пришли к выводу, что….. и сформулировали правило….

Две другие группы заполняют таблицу за выступающими.

Учитель: Существует ли функция, которая одновременно является нечётной и чётной?

Ученики: Существует у(х)=0.

V . Закрепление полученных знаний. (6 мин.) Проверочная работа (Приложение 3).

VI. Подведение итогов урока и информация о домашнем задании (2 мин.).

Какие цели мы ставили в начале урока? Выполнили задуманное? Молодцы, нам удалось выполнить цели урока, потому что вы были внимательны, сосредоточены и активны. За активную работу устно и у доски следующие учащиеся получили отметки:______________.

Домашнее задание: подготовить по две функции с доказательством чётности (нечётности) на каждое правило. Уровень сложности составленных функций будет учитываться.

VII. Рефлексия (2 мин.).

У Вас у каждого на столах лежит по 2 смайлика. Один улыбающий, который обозначает радость, успех, удовольствие, интерес. А другой – грустный, обозначает трудности, преграды, разочарование. Если вам на уроке было интересно, понятно, то прикрепите смайлик с улыбкой к вашей работе. А если трудно и что-то осталось непонятно, то грустного смайлика.

Источник