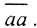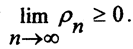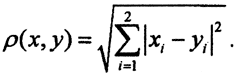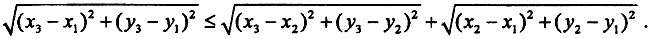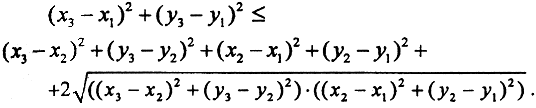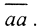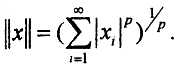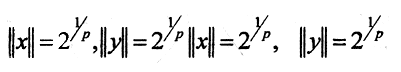Доказать что пространство неполное

задан 18 Ноя ’15 20:37

Ni55aN
65 ● 4 ● 17
80&#037 принятых

2 ответа

Совершенно неверно то, что все последовательности фундаментальны. Видимо, это просто оговорка. Полным называется метрическое пространство, в котором каждая ф.п. сходится к некоторому элементу этого же пространства.

Следует также помнить, что на практике часто приходится решать сложные уравнения (например, дифференциальные), которые не решаются аналитически. Тогда приходится применять приближённые методы, и встаёт вопрос о степени точности. Допустим, мы получаем серию каких-то решений, постепенно повышая точность, и видим, что решения почти «стабилизировались». Это соответствует интуитивному смыслу того, что последовательность фундаментальна. Если мы знаем, что она сходится, то тогда её предел и есть решение, то есть можно считать, что оно найдено.

Важен при этом тот факт, что сравнивать по степени близости приходится более сложные объекты нежели числа или точки плоскости. При решении дифференциальных уравнений (а они описывают физические и прочие процессы) сравнивать по степени «близости» приходится функции, изучая метрические пространства функций и их свойства. Для этого надо научиться работать в «непривычных» метриках любого сорта. Понимая при этом, какие свойства являются общими для всех метрик, а какие для данных специфических метрик.

Вообще, проще всего считать, что применимо ВСЁ. Это так и есть на самом деле.

В разного рода сложных пространствах функций может быть как полнота, так и неполнота. Если пространство не полно, то его часто пытаются расширить до полного, что обычно оказывается возможным, но получается ещё более сложный объект (в том же смысле, как действительные числа сложнее рациональных). С другой стороны, с ними проще работать. Для рациональных чисел мы бы не могли определить синусы или логарифмы.

3) Выводы состоят в том, что в полном метрическом пространстве можно переходить к пределу, а в неполном это уже не так. По сути дела, на этот вопрос было отвечено выше. Если имелось в виду, как отличить полное пространство от неполного, то это в каждом отдельном случае надо исследовать своими способами, и такая задача может быть сложной. Поэтому и развивают общую теорию для изучения этого рода вещей.

Источник

II. Основные теоремы о пространствах

2.1. Полные метрические пространства

Теорема 1 (Критерий полноты Кантора). Метрическое пространство полно, если и только если любая последовательность непустых вложенных замкнутых шаров, радиусы которых стремятся к нулю, имеет непустое пересечение.

Необходимость. Пусть последовательность вложенных шаров при r_{n →∞}→0 и пространство (X,ρ) полное. Тогда существует и единственна точка x₀, принадлежащая всем шарам сразу. Рассмотрим последовательность n> центров этих шаров и оценим расстояние ρ(x_n,x_m) при m>n. Так как при , но по условию теоремы r_n→0, стало быть и ρ(x_n,x_m)→0 при n,m→∞. То есть последовательность n> фундаментальна и в силу полноты пространства сходится. Члены её, начиная с m-го, принадлежат шару так как шар замкнутый, то и предел принадлежит этому шару, а то есть пересечение шаров не пусто.

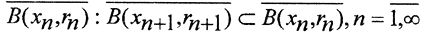
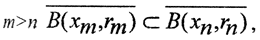
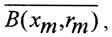
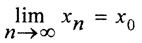
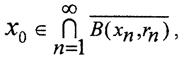
Пример. Может ли в банаховом пространстве иметь пустое пересечение последовательность непустых вложенных замкнутых множеств?

Да, может. Рассмотрим банахово пространство вещественных чисел R и последовательность непустых замкнутых вложенных множеств в нем x_i = [i,∞), i=1,∞. Ясно, что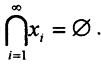

Пример. Множество рациональных чисел есть множество I категории.

Теорема 2 (Теорема Бэра о категориях). Носитель X полного метрического пространства (X,ρ) есть множество II категории.

( Комментарий. Ясно, что в полном метрическом пространстве всякое не пустое открытое множество есть множество второй категории, а множества, дополнительные к множествам первой категории, тоже множества второй категории.)

Определение 2. Полное метрическое пространство (Y,ρ_y) называется пополнением метрического пространства (X,ρ_x), если пространство (X,ρ_x) всюду плотно в пространстве (Y,ρ_y).

Определение 3. Пространства (X,ρ_x) и (Y,ρ_y) называют изомерными, если между ними существует хоть одна биекция и ρ_y = ρ_x.

Теорема 3 (Теорема Хаусдорфа о пополнении метрических пространств). Любое неполное метрическое пространство (X,ρ_x) имеет единственное с точностью до изомерности пополнение.

1. Из элементов данного неполного метрического пространства (X,ρ_x) построим некоторое пространство (Y,ρ_y).

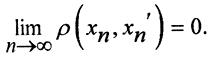
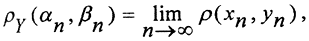
Фундаментальные последовательности n> и n> метрического пространства (X,ρ) назовём конфинальными, если Конфинальность определяет отношение эквивалентности x_nx’_n, то есть это отношение рефлексивно, симметрично и транзитивно. Рефлексивность и симметричность очевидны, а из неравенства треугольника следует транзитивность. Действительно, пусть x_nx’_n, а x’_nx»_n. Тогда ρ(x_n,x»_n)≤ρ(x_n,x’_n)+ρ(x’_n,x»_n). Если ρ(x_n,x’_n)→0 и ρ(x’_n,x»_n)→0, то ρ(x_n,x»_n)→0. Отношение эквивалентности разбивает фундаментальные последовательности пространства (X,ρ_x) на непересекающиеся классы эквивалентных между собой последовательностей. Таким образом мы получили новое фактор-множество Y, элементами которого являются непересекающиеся классы фундаментальных последовательностей <α_n>, <β_n>, <γ_n>. представителями которых являются фундаментальные последовательности n>, n>, n>. пространства (X,ρ_x). Если фундаментальная последовательность n> сходится к точке x, то и эквивалентная ей последовательность <α_n> сходится к той же точке. Действительно, пусть ρ(x_n,x)|_n→∞→0. Тогда ρ(α_n,x)≤ρ(α_n,x_n)+ρ(x_n,x)→0 и ρ(α_n,x)|_n→∞→0. Будем рассматривать фактор-множество Y как носитель нового метрического пространства (Y,ρ_y) с метрикой , если, конечно, удастся доказать, что это метрика.

2.1. Существование. Достаточно показать, что последовательность <ρ_n(x_n,y_n)> фундаментальна, тогда, в силу полноты числовой оси, она сходится. Полнота числовой оси доказывается независимо.

Лемма 1 (О четырёх точках). Для любых четырёх точек x,x’,y,y’ метрического пространства Х справедливо неравенство |ρ(x,y)-ρ(x’,y’)|≤ρ(x,x’)+ρ(y,y’).

ρ(x,y)≤ρ(x,x’)+ρ(x’,y)≤ρ(x,x’)+ρ(x’,y’)+ρ(y’,y) ⇒ ρ(x,y)-ρ(x’,y’)≤ρ(x,x’)+ρ(y,y’). Поменяв местами x,y и x’,y’, получим ρ(x’,y’)-ρ(x,y)≤ρ(x’,x)+ρ(y’,y).

Отсюда сразу |ρ(x,y)-ρ(x’,y’)|≤ρ(x,x’)+ρ(y,y’).

Лемма 2 (О непрерывности метрики). Метрика ρ(x,y) является непрерывной функцией своих аргументов.

Из леммы 1 |ρ(x_n,y_n)-ρ(x,y)|≤ρ(x_n,x)+ρ(y_n,y)→0 при n→∞, то есть если ρ(x_n,x)→0 и ρ(y_n,y)→0 при n→∞, то ρ(x_n,y_n)→ρ(x,y).

Доказательство существования метрического пространства (Y,ρ_y).

Если последовательности n> и n> фундаментальные, то ρ(x_n,x_m)→0 и ρ(y_n,y_m)→0 при m,n→∞. Тогда согласно лемме о четырёх точках можно записать соотношение: |ρ(x_n,y_n)-ρ(x_m,y_m)|≤ρ(x_n,x_m)+ρ(y_n,y_m)→0 при m,n→∞. То есть числовая последовательность <ρ_n(x_n,y_n)> фундаментальна и, следовательно, и сходится в полном пространстве R 1 ₁.

2.2. Доказательство независимости от выбора представителей.

2.3. Проверим выполнение аксиом метрики.

1. По свойствам пределов, связанных с неравенствами, если все члены последовательности <ρ_n(x_n,y_n)>≥0, то и

2. Симметричность очевидна.

3. Докажем аксиому треугольника. Так как ∀ n ρ(x_n,y_n)≤ρ(x_n,z_n)+ρ(z_n,y_n), то, по свойствам пределов, связанных с неравенствами и непрерывности метрики сразу получаем что и третья аксиома справедлива. Таким образом, пространство (Y,ρ_y) метрическое.

3. Покажем, что метрическое пространство (Y,ρ_y) и есть пополнение метрического пространства (X,ρ_x).

Надо показать, что: метрическое пространство (X,ρ_x) всюду плотно в метрическом пространстве (Y,ρ_y) и эти пространства изомерны.

3.1. Покажем, что метрическое пространство (X,ρ_x) всюду плотно в метрическом пространстве (Y,ρ_y).

3.2. Покажем, что метрическое пространство (Y,ρ_y) полно.

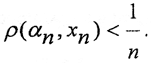
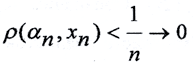
Рассмотрим некоторую фундаментальную последовательность <α_n>∈Y. Так как пространство (X,ρ_X) всюду плотно в (Y,ρ_y), то для каждого номера n найдётся элемент x_n∈X такой, что Тогда из неравенства треугольника следует соотношение ρ(x_n,x_m)≤ρ(x_n,α_n)+ρα_n,x_m) 1 ₁, то есть ρ_y(α₀,x_n)→0. Таким образом, метрическое пространство (Y,ρ_Y) полно.

3.3. Покажем, что метрическое пространство (Y,ρ_Y) является единственным с точностью до изоморфизма пополнением метрического пространства (X,ρ_X).

Источник

Доказать что пространство неполное

1.4.3. Стандартные метрические пространства

Пример 1. На плоскости R 2 для точек A(x₁, y₁) и B(x₂, y₂) определим расстояние тремя различными способами и покажем, что введенные расстояния являются метриками, то есть проверим выполнимость аксиом.

1.Метрика 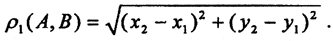. Это евклидова метрика при p = 2

Первые аксиомы очевидны. Проверим третью аксиому. Рассмотрим точки A(x₁, y₁), B(x₂, y₂) и C(x₃, y₃) докажем следующее неравенство:

Возведем это неравенство в квадрат:

Так как (x₃-x₁) 2 ≤(x₃-x₂) 2 +(x₂-x₁) 2 и (y₃-y₁) 2 ≤(y₃-y₂) 2 +(y₂-y₁) 2 (поскольку (b-a) 2 )≤b 2 +a 2 ) и выражение 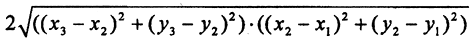неотрицательно, то неравенство является верным.

2. Метрика ρ₂(A,B) = max<|y₂-y₁|, |x₂-x₁|>. Это двумерное арифметическое пространство с супремальной метрикой. Первые аксиомы очевидны. Проверим третью аксиому.

( Комментарий. 1. Понятие пополнения употреблено впрок и будет определено позднее.

2. Любое нормированное пространство является метрическим с метрикой ρ = ||x-y||. Выполнение первых аксиом очевидно. Третья выполняется в силу ||x-y||=||(x-z)+(z-y)||≤||x-z||+||z-y||. Обратное, вообще говоря, неверно, то есть метрические пространства, вообще говоря, не являются нормированными. Но если потребовать, чтобы метрическое пространство обладало инвариантностью относительно сдвигов, то есть ρ(x+z,y+z) = ρ(x,y) и однородностью относительно растяжений, то есть ρ(αx,αy) = |α|ρ(x,y), то тогда верно и обратное, и норма элемента есть метрика, второй элемент которой есть ноль.

Для стандартных метрических пространств это так, так что все вышеприведённые примеры являются одновременно и примерами стандартных норм с геометрией, отличной от эвклидовой. Единичные шары в этих метриках изображены в примере 3.)

Пример 2. Покажем, что ρ = arctg|x-y| является метрикой. Выполнение первых двух аксиом метрики очевидно. Чтобы проверить третью, то есть arctg|x-z+z-y|≤arctg|x-z|+arctg|z-y|, докажем, что для любых α,β ≥0имеет место неравенство arctg(α+β)≤arctgα+arctgβ.

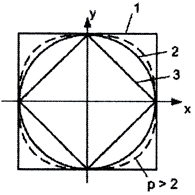
Пример 3. Рассмотрим пространство R 2 _p. Положив y = 0, а ρ = 1, мы получим единичную сферу в пространстве R 2 _p.

При p = 1 уравнение этой сферы имеет вид ||x||₁ = |x|+|y| = 1, и такая метрика называется октаэдрической, потому что единичной сферой в трёхмерном случае ||x||₁ = |x|+|y|+|z| = 1 будет октаэдр.

При p = 2 уравнение этой сферы имеет вид 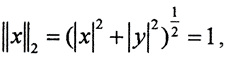и такая метрика называется евклидовой (сферической), потому что единичной сферой в трёхмерном случае будет обычная сфера.

Чебышёвская (кубическая) метрика: ||x||_∞ = max<|x|,|y|>, потому что единичной сферой в трёхмерном случае ||x||_∞ = max <|x|,|y|,|z|>= 1 будет куб.

Пусть неверно, что ρ(x,y)≤ρ(x,z)+ρ(z,y). Тогда ρ(x,y) = 1.⇒x ≠y. Но тогда ρ(x,z)+ρ(z,y) = 0, то есть x=y.

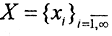
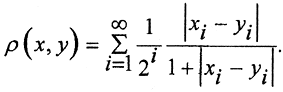
2. Ограниченные последовательности с метрикой Проверим третью аксиому.

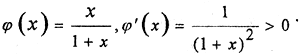
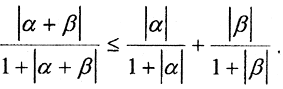
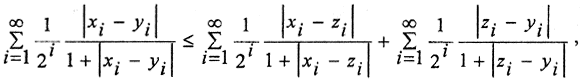
Рассмотрим возрастающую функцию Так как |α+β|≤|α|+|β|, то φ(|α+β|)≤φ(|α|)+φ(|β|), то есть Пусть α = x_i-z_i, β = z_i-y_i, тогда α+β = x_i-y_i. Теперь или ρ(x,y)≤ρ(x,z)+ρ(z,y).

В этой метрике при m ρ(m, n₂) то есть натуральные числа, чем дальше они расположены на числовой оси, тем ближе по метрике ρ.

Ясно, что равенство параллелограмма не выполнено при p≠2.

5. Покажем, что пространство C[0,1] не гильбертово.

Пространство C[0,1] полное нормированное пространство, то есть банахово. (Полноту покажем в следующем пункте.) Уже отмечалось, что норма порождается скалярным произведением, если и только если выполняется равенство параллелограмма ||x+y|| 2 +||x-y|| 2 = 2(||x|| 2 +||y|| 2 ). Пусть x(t) = 1, y(t) = t. Тогда, вычисляя норму в пространстве C[0,1], сразу получим ||t+1|| 2 +||t-1|| 2 = 2 2 +1 2 ≠2(1 2 +1 2 ).

6. Будет ли нормированным пространством линейное пространство непрерывно дифференцируемых функций, если на нём в качестве нормы использовать норму пространства непрерывных функций C[0,1]?

Да. Проверим аксиоматику:

3)||x(t)+y(t)||_t∈[a,b] = max_t∈[a,b]|x(t)+y(t)|≤ max_t∈[a,b](|x(t)|+|y(t)|)≤ max_t∈[a,b]|x(t)|+max_t∈[a,b]|y(t)| = ||x(t)||_t∈[a,b]+||y(t)||_t∈[a,b].

7. Будет ли нормированным пространством линейное пространство непрерывно дифференцируемых функций, если на нём в качестве нормы использовать норму ||x(t)||_t∈[a,b] = max_t∈[a,b]|x'(t)|?

8. Доказать, что подпространство B₁ банахова пространства B является банаховым пространством.

Источник

Теория функций действительного переменного/Полные метрические пространства

Определение и примеры [ править ]

Метрическое пространство (M, ρ) называется полным, если любая его фундаментальная последовательность сходится к элементу этого пространства.

Рассмотрим несколько примеров.

Пример 2. Пусть M = (0; 1), ρ(x, y)=|x-y|. Рассмотрим последовательность

является примером фундаментальной последовательности элементов множества M, которая не сходится в M.

Как известно из математического анализа:

lim n → ∞ ( 1 + 1 n ) n = e ∉ Q <\displaystyle \lim _\left(1+<\frac <1>>\right)^=e\notin \mathbb > .

ρ = ∑ i = 1 n ( x i − y i ) 2 <\displaystyle \rho =<\sqrt <\sum _^(x_-y_)^<2>>>> .

Рассмотрим фунментальную последовательность

(здесь номера членов последовательности обозначены индексом в скобках наверху). По определению фундаментальной последовательности,

∑ i = 1 n ( x i ( k ) − x i ( m ) ) 2 ϵ <\displaystyle <\sqrt <\sum _^\left(x_^<(k)>-x_^<(m)>\right)^<2>>> .

| x n ( t ) − x m ( t ) | ϵ <\displaystyle |x_(t)-x_(t)| ,

это означает, что последовательность < x n ( t ) ><\displaystyle \(t)\>> сходится равномерно, а так как предел равномерно сходящейся последовательности непрерывных функций есть непрерывная функция

x ( t ) = lim n → ∞ x n ( t ) <\displaystyle x(t)=\lim _x_(t)>

Если в неравенстве

| x n ( t ) − x m ( t ) | ϵ <\displaystyle |x_(t)-x_(t)| ,

Пример 6. Покажем что пространство непрерывных функций C 2 [ − 1 ; 1 ] <\displaystyle C_<2>[-1;1]> не является полным. Рассмотрим последовательность непрерывных функций вида

Последовательность < g n ><\displaystyle \\>> является фундаментальной. Действительно, рассмотрим две функции g n <\displaystyle g_> и g m <\displaystyle g_> , они отличаются друг от друга лишь на отрезке ширины

причём абсолютная величина различия не превышает 1, следовательно

Однако последовательность < g n ><\displaystyle \\>> не сходится ни к одной непрерывной функции из C 2 [ 0 ; 1 ] <\displaystyle C_<2>[0;1]> . Для доказательства этого факта рассмотрим произвольную функцию f ∈ C 2 [ − 1 ; 1 ] <\displaystyle f\in C_<2>[-1;1]> и разрывную функцию

В силу интегрального неравенства Минковского (это неравенство справедливо и для кусочно-непрерывных функций):

∫ − 1 1 [ f ( t ) − g ( t ) ] 2 d t ≤ ∫ − 1 1 [ f ( t ) − g n ( t ) ] 2 d t + ∫ − 1 1 [ g n ( t ) − g ( t ) ] 2 d t <\displaystyle <\sqrt <\int \limits _<-1>^<1>[f(t)-g(t)]^<2>dt>>\leq <\sqrt <\int \limits _<-1>^<1>[f(t)-g_(t)]^<2>dt>>+<\sqrt <\int \limits _<-1>^<1>[g_(t)-g(t)]^<2>dt>>> .

∫ − 1 1 [ g n ( t ) − g ( t ) ] 2 d t ≤ 2 n <\displaystyle \int \limits _<-1>^<1>[g_(t)-g(t)]^<2>dt\leq <\frac <2>>>

lim n → ∞ ∫ − 1 1 [ g n ( t ) − g ( t ) ] 2 d t = 0 <\displaystyle \lim _\int \limits _<-1>^<1>[g_(t)-g(t)]^<2>dt=0> .

Теоремы о полных пространствах [ править ]

Теорема 2 (о вложенных шарах). Для того, чтобы метрическое пространство было полным необходимо и достаточно, чтобы в нём всякая последовательность вложенных друг в друга замкнутых шаров, радиусы которых стремятся к нулю, имела непустое пересечение.

Последовательность центров x n <\displaystyle x_> является фундаментальной, так как

По определению пересечения множеств

Следующий номер n_<1>>»> n 2 > n 1 <\displaystyle n_<2>>n_<1>> n_<1>>»/> выберем таким образом, чтобы при n_<2>>»> n > n 2 <\displaystyle n>n_<2>> n_<2>>»/> выполнялось неравенство

Пусть мы уже выбрали номера

Номер n_>»> n k + 1 > n k <\displaystyle n_>n_> n_>»/> выберем так, чтобы при n_>»> n > n k + 1 <\displaystyle n>n_> n_>»/> выполнялось неравенство

Доказательство проведём от противного.

и так далее. Таким образом можно получить последовательность вложенных друг в друга замкнутых шаров

радиусы которых стремятся к нулю, причём

По теореме о вложенных шарах пересечение

что противоречит исходному предположению. Теорема доказана.

Пополнение метрического пространства [ править ]

Полнота пространства является очень важным с точки зрения анализа свойством, так как в неполных пространствах не все фундаментальные последовательности имеют предел. Возникает вопрос: можно ли расширить неполное пространство таким образом, чтобы оно стало полным. Оказывается, что это всегда можно сделать, причём такое расширение является, по-существу, единственным.

Напомним, что множество

называется всюду плотным в M, если имеет место равенство

Справедлива следующая теорема:

Обозначать факт эквивалентности двух последовательностей будем следующим образом:

\\>\sim \\>> .

Используя аксиомы метрики, можно показать, что введённое нами отношение эквивалентности двух последовательностей является рефлексивным, симметричным и транзитивным.

\\>\in \eta _<2>>

В силу неравенства четырёхугольника:

По неравенству четырёхугольника

\\>\sim \\>> ,

то по введённому определению эквивалентности

Таким образом, значение предела действительно не зависит от выбора последовательности.

Для доказательства аксиомы треугольника рассмотрим три класса эквивалентности

\eta _<3>\in R’> .

Выберем в каждом из этих классов по одной последовательности

Переходя в этом неравенстве к пределу, получим

y=\lim _y_> ,

Тогда при n_<0>>»> n > n 0 <\displaystyle n>n_<0>> n_<0>>»/> будем иметь

\lim _y_=y’> ,

а в пространстве R 2 <\displaystyle R_<2>>

\lim _y_=y»> ,

то в силу непрерывности метрики

Источник