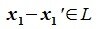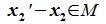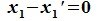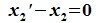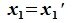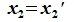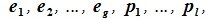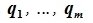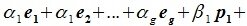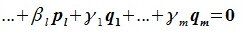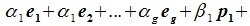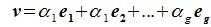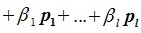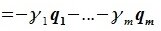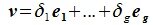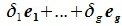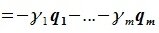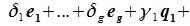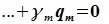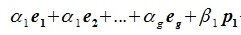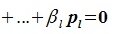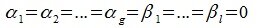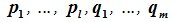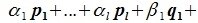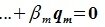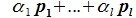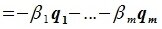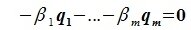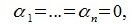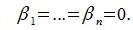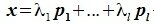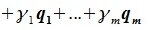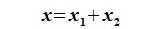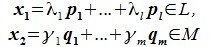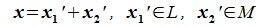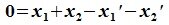Доказать что пространство rn есть прямая сумма двух линейных подпространств

18.04.202223.04.2022 admin 0 Comments

Прямая сумма подпространств, натянутых на системы векторов

Проверить, что подпространства L1 и L2, натянутые на системы векторов x₁=(2,3,11,5), x₂=(1,1,5,2), x₃=(0,1,1,1) и y₁=(2,1,3,2), y₂=(1,1,3,4), y₃=(5,2,6,2) соответственно, дают в прямой сумме все подпространство A₄, и найти разложение вектора x=(2,0,0,3) по этим подпространствам.

Правильно ли я понимаю, что чтобы ответить на первый вопрос, нужно найти базис суммы подпространств и если его размерность равна 4, то ответ верный (L1 и L2 дают в прямой сумме все подпространство A₄)?

А вот как найти разложение вектора по подпространствам, я не понимаю. Помогите, пожалуйста!

Прямая сумма подпространств
Помогите разобраться. Задачка такая: доказать, что пространство V многочленов степени не выше n.

Прямая сумма подпространств
Доказать, что 4-мерное арифметическое пространство является прямой суммой линейных подпространств.

Прямая сумма подпространств
Здравствуйте! Нужно показать, что пространство M_2(\mathbb) является прямой суммой.

То есть, мне нужно найти только коэффициенты? и всё?

Источник

Прямая сумма подпространств

видно что столбцы образуют базис в пространстве
При этом ни один из векторов нельзя выразить через вектора, и наоборот, т.к. они линейно независимы.

Вроде кажется что все верно, но грамотно сформулировать мысль не могу, помогите пожалуйста.

Прямая сумма подпространств, натянутых на системы векторов
Проверить, что подпространства L1 и L2, натянутые на системы векторов x1=(2,3,11,5), x2=(1,1,5,2).

Сумма подпространств
Пусть задана сумма подпространств V = _<1>+_ <2>, нужно доказать что если запись X =.

Решение

Прямая сумма и прямое произведение групп
В чём принципиальное отличие прямого произведения от прямой суммы? Я если честно эти понятия не.

Структуры (Создайте структуру Прямая с элементами x1, y1, x2, y2 – координаты двух точек, через которые проходит прямая)
Создайте структуру Прямая с элементами x1, y1, x2, y2 – координаты двух точек, через которые.

В автокаде прямая линия не всегда прямая
Почему то получается иногда в автокаде так, что прямая линия имеет дефекты, какие то шреховатости.

Описание алгоритмов «математическая прямая», «рекуррентная прямая», «прямая Брезенхейма»
Доброго времени суток. Есть задача, нарисовать прямые используя следующие алгоритмы «математическая.

Источник

Подпространство линейного пространства

Определение и размерность подпространства

Определение 6.1. Подпространством L n-мерного пространства R называется множество векторов, образующих линейное пространство по отношению к действиям, которые определены в R.

Другими словами, L называется подпространством пространства R, если из x, y∈L следует, что x+y∈L и если x∈L, то λ x∈L, где λ— любое вещественное число.

Простейшим примером подпространства является нулевое подпространство, т.е. подмножество пространства R, состоящее из единственного нулевого элемента. Подпространством может служить и все пространство R. Эти подпространства называются тривиальными или несобственными.

Подпространство n-мерного пространства конечномерно и его размерность не превосходит n: dim L≤ dim R.

Сумма и пересечение подпространств

Cуммой L+M называется множество векторов x+y, где x∈L и y∈M. Очевидно, что любая линейная комбинация векторов из L+M принадлежит L+M, следовательно L+M является подпространством пространства R (может совпадать с пространством R).

Пересечением L∩M подпространств L и M называется множество векторов, принадлежащих одновременно подпространствам L и M (может состоять только из нулевого вектора).

Теорема 6.1. Сумма размерностей произвольных подпространств L и M конечномерного линейного пространства R равна размерности суммы этих подпространств и размерности пересечения этих подпространств:

dim L+dim M=dim(L+M)+dim(L∩M).

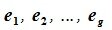
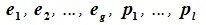
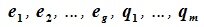
Доказательство. Обозначим F=L+M и G=L∩M. Пусть G g-мерное подпространство. Выберем в нем базис . Так как G⊂L и G⊂M, следовательно базис G можно дополнить до базиса L и до базиса M. Пусть базис подпространства L и пусть базис подпространства M. Покажем, что векторы

составляют базис F=L+M. Для того, чтобы векторы (6.1) составляли базис пространства F они должны быть линейно независимы и любой вектор пространства F можно представить линейной комбинацией векторов (6.1).

Докажем линейную независимость векторов (6.1). Пусть нулевой вектор пространства F представляется линейной комбинацией векторов (6.1) с некоторыми коэффициентами:

Левая часть (6.3) является вектором подпространства L, а правая часть является вектором подпространства M. Следовательно вектор

принадлежит подпространству G=L∩M. С другой стороны вектор v можно представить линейной комбинацией базисных векторов подпространства G:

Из уравнений (6.4) и (6.5) имеем:

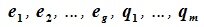
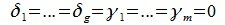
Но векторы являются базисом подпространства M, следовательно они линейно независимы и . Тогда (6.2) примет вид:

В силу линейной независимости базиса подпространства L имеем:

Так как все коэффициенты в уравнении (6.2) оказались нулевыми, то векторы

Изучая базисы подпространств L и M и базис подпространства F=L+M (6.10), имеем: dim L=g+l, dim M=g+m, dim (L+M)=g+l+m. Следовательно:

dim L+dim M−dim(L∩M)=dim(L+M). ■

Прямая сумма подпространств

Определение 6.2. Пространство F представляет собой прямую сумму подпространств L и M, если каждый вектор x пространства F может быть единственным способом представлен в виде суммы x=y+z, где y∈ L и z∈M.

Прямая сумма обозначается L⊕M. Говорят, что если F=L⊕M, то F разлагается в прямую сумму своих подпространств L и M.

Теорема 6.2. Для того, чтобы n-мерное пространство R представляло собой прямую сумму подпространств L и M, достаточно, чтобы пересечение L и M содержало только нулевой элемент и чтобы размерность R была равна сумме размерностей подпространств L и M.

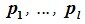
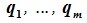
Доказательство. Выберем некоторый базис в подпространстве L и некоторый базис в подпространстве M. Докажем, что

является базисом пространства R. По условию теоремы размерность пространства R n равна сумме подпространств L и M (n=l+m). Достаточно доказать линейную независимость элементов (6.11). Пусть нулевой вектор пространства R представляется линейной комбинацией векторов (6.11) с некоторыми коэффициентами:

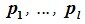
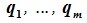
Но векторы и являются базисами подпространств L и M соответственно. Следовательно они линейно независимы. Тогда

Установили, что (6.12) справедливо лишь при условии (6.15), а это доказывает линейную независимость векторов (6.11). Следовательно они образуют базис в R.

Пусть x∈R. Разложим его по базису (6.11):

Из (6.17) и (6.18) следует, что любой вектор из R можно представить суммой векторов x₁∈L и x₂∈M. Остается доказать что это представление является единственным. Пусть кроме представления (6.17) есть и следующее представление: