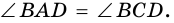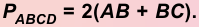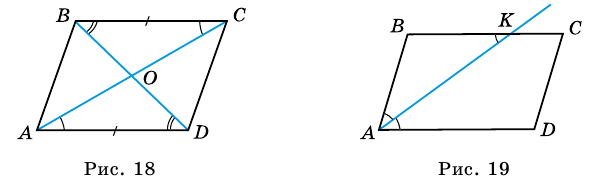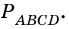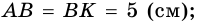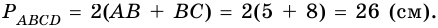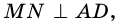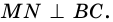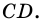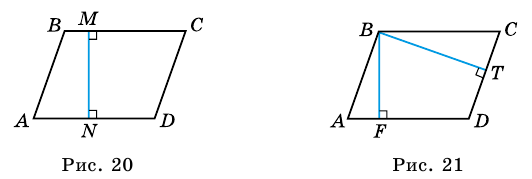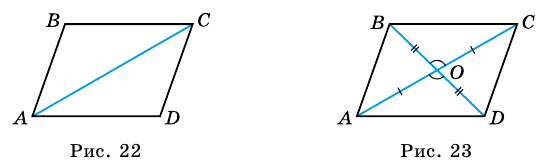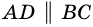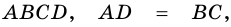Доказать что противоположные стороны параллелограмма равны

Параллелограмм. Свойства и признаки параллелограмма

Определение параллелограмма

Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.

Свойства параллелограмма

1. Противоположные стороны параллелограмма попарно равны

2. Противоположные углы параллелограмма попарно равны

3. Сумма смежных (соседних) углов параллелограмма равна 180 градусов

4. Сумма всех углов равна 360°

5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам

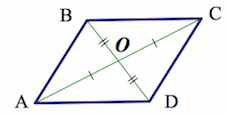
6. Точка пересечения диагоналей является центром симметрии параллелограмма

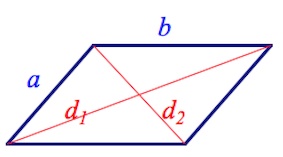
7. Диагонали параллелограмма и стороны
связаны следующим соотношением:

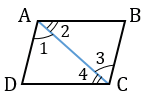
8. Биссектриса отсекает от параллелограмма равнобедренный треугольник

Признаки параллелограмма

Четырехугольник является параллелограммом, если выполняется хотя бы одно из следующих условий:

1. Противоположные стороны попарно равны:

2. Противоположные углы попарно равны:

3. Диагонали пересекаются и в точке пересечения делятся пополам

4. Противоположные стороны равны и параллельны:

5.

Небольшой видеоролик о свойствах параллелограмма (в том числе ромба, прямоугольника, квадрата) и о том, как эти свойства применяются в задачах:

Формулы площади параллелограмма смотрите здесь.

Хорошую подборку задач на нахождение углов и длин в параллелограмме смотрите здесь.

Источник

Признаки параллелограмма

Доказательство:

Дано: АВСD — четырехугольник, АD = ВС, АDВС.

Доказать: АВСD — параллелограмм.

Доказательство:

1. Проведем диагональ АС четырехугольника АВСD.

Доказательство:

Доказать: АВСD — параллелограмм.

Доказательство:

1. Проведем диагональ АС четырехугольника АВСD.

3. Итак, АD = ВC, АDВС, по 1 0 признаку параллелограмма, четырехугольник АВСD — параллелограмм. Что и требовалось доказать.

Доказательство:

Доказать: АВСD — параллелограмм.

Доказательство:

1. Рассмотрим АОD и ВОС: по условию АО = ОС, DО = ОВ, АОD и ВОС (как вертикальные углы), АОD =ВОС (по 1 признаку равенства треугольников), АD = ВC и 1 = 2.

2. 1 и 2 накрест лежащие при пересечении прямых АD и ВC секущей АС, при этом 1 = 2, по признаку параллельности двух прямых АDВС.

3. Итак, АD = ВC, АDВС, по 1 0 признаку параллелограмма, четырехугольник АВСD — параллелограмм. Что и требовалось доказать.

Поделись с друзьями в социальных сетях:

Источник

Признаки параллелограмма

Признаки параллелограмма — это признаки,
с помощью которых можно доказать,
что четырехугольник — параллелограмм.

Чтобы доказать, что четырехугольник — параллелограмм, нужно знать признаки
параллелограмма. Четырехугольник является параллелограммом, если один
из признаков параллелограмма для этого четырехугольника истинен.
Например, если у четырехугольника две стороны равны и
параллельны, значит этот четырехугольник параллелограмм.

Всего существует три признака параллелограмма: по двум одинаковым
параллельным сторонам, по пересечению диагоналей и делению
диагоналей пополам в точке пересечения, по попарно равным
противоположным сторонам. В этой статье мы рассмотрим
все три признака параллелограмма.

I признак параллелограмма

По пересечению диагоналей и делению
диагоналей в точке пересечения пополам.

Четырехугольник является параллелограммом, если у четырехугольника
диагонали пересекаются, и в точке пересечения делятся пополам.

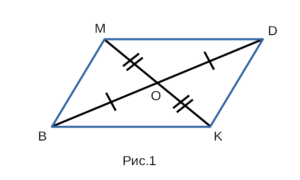
Если на рисунке 1 — BO = OD, MO = OK, то BMDK — параллелограмм.

II признак параллелограмма

По двум одинаковым параллельным сторонам.

Четырехугольник является параллелограммом, если у четырехугольника
две стороны равны и параллельны.

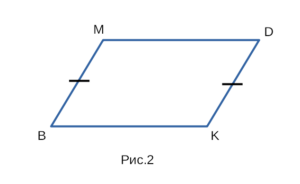
Если на рисунке 2 — BM = DK, BM || DK, то BMDK — параллелограмм.

III признак параллелограмма

По попарно равным противоположным сторонам.

Четырехугольник является параллелограммом, если у
четырехугольника противоположные стороны попарно равны.

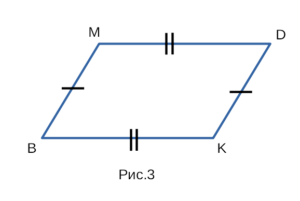
Если на рисунке 3 — BM = DK, MD = BK, то BMDK — параллелограмм.

В этой статье мы рассмотрели все три признака параллелограмма и
теперь можем доказать, что некий четырехугольник параллелограмм.

В следующей статье про площадь параллелограмма вы узнакете как её расчитать.

Источник

Параллелограмм, его свойства и признаки с примерами решения

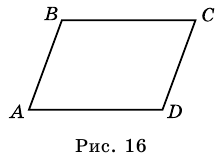
Параллелограммом называют четырехугольник, у которого противолежащие стороны попарно параллельны.

На рисунке 16 изображен параллелограмм

Рассмотрим свойства параллелограмма.

1. Сумма двух любых соседних углов параллелограмма равна 180°.

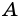
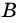
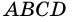
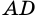
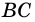
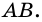
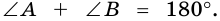
Действительно, углы и параллелограмма (рис. 16) являются внутренними односторонними углами для параллельных прямых и и секущей Поэтому Аналогично это свойство можно доказать для любой другой пары соседних углов параллелограмма.

2. Параллелограмм является выпуклым четырехугольником.

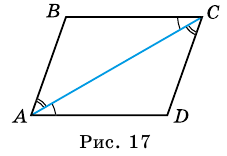
3. В параллелограмме противолежащие стороны равны и противолежащие углы равны.

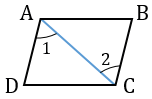
Доказательство:

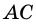
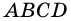
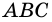
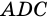
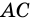
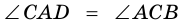
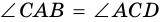
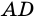
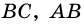
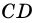
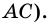
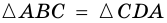
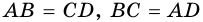
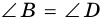
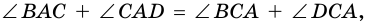
Диагональ разбивает параллелограмм на два треугольника и (рис. 17). -их общая сторона, и (как внутренние накрест лежащие углы для каждой из пар параллельных прямых и и и секущей Тогда (по стороне и двум прилежащим углам). Откуда, и (как соответственные элементы равных треугольников). Так как то

4. Периметр параллелограмма

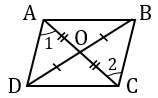
5. Диагонали параллелограмма точкой пересечения делятся пополам.

Доказательство:

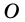
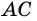
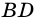
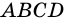
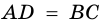
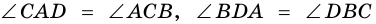
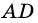
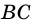
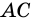
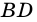
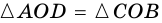
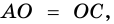
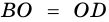
Пусть — точка пересечения диагоналей и параллелограмма (рис. 18). (как противолежащие стороны параллелограмма), (как внутренние накрест лежащие углы для параллельных прямых и и секущих и соответственно). Следовательно, (по стороне и двум прилежащим углам). Тогда (как соответственные стороны равных треугольников).

Пример:

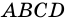
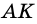
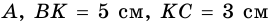
Дано: параллелограмм, — биссектриса угла (рис. 19). Найдите:

Решение:

1)

2) (как внутренние накрест лежащие углы для параллельных прямых и и секущей

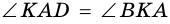
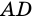
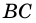
3) (по условию), тогда Тогда — равнобедренный (по признаку равнобедренного треугольника),

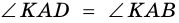
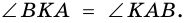
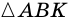
4)

Высотой параллелограмма называют перпендикуляр, проведенный из любой точки стороны параллелограмма к прямой, содержащей противолежащую сторону.

На рисунке 20 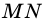— высота параллелограмма,

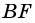
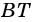
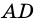
Из каждой вершины параллелограмма можно провести две высоты. Например, на рисунке 21 и — высоты параллелограмма, проведенные соответственно к сторонам и

Рассмотрим признаки параллелограмма.

Теорема (признаки параллелограмма). Если в четырехугольнике: 1) две стороны параллельны и равны, или 2) противолежащие стороны попарно равны, или 3) диагонали точкой пересечения делятся пополам, или 4) противолежащие углы попарно равны, — то четырехугольник является параллелограммом.

Доказательство:

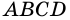
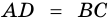
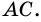
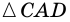
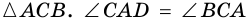
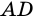
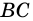
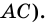
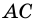
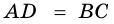
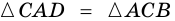
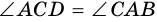
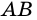
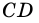
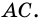
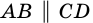
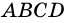
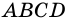
1) Пусть в четырехугольнике и (рис. 22). Проведем диагональ Рассмотрим и (как внутренние накрест лежащие при параллельных прямых и и секущей — общая сторона, (по условию). Следовательно, (по двум сторонам и углу между ними). Тогда (как соответственные). Но это накрест лежащие углы при пересечении прямых и секущей Поэтому (по признаку параллельности прямых). Следовательно, в четырехугольнике противолежащие стороны попарно параллельны. Поэтому -параллелограмм.

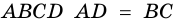
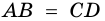
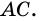
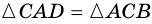
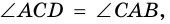
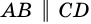
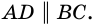
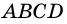
2) Пусть в четырехугольнике и (рис. 22). Проведем диагональ Тогда (по трем сторонам). Поэтому и следовательно, (по признаку параллельности прямых). Аналогично доказываем, что Следовательно, — параллелограмм.

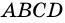
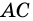
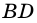
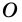
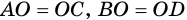
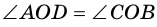
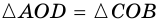
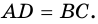
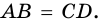
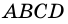
3) Пусть в четырехугольнике диагонали и пересекаются в точке и (рис. 23). (как вертикальные). Поэтому (по двум сторонам и углу между ними). Отсюда Аналогично доказываем, что Принимая во внимание п. 2) этой теоремы, приходим к выводу, что — параллелограмм.

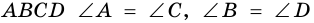
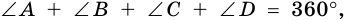
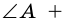
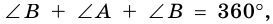
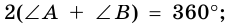
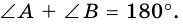
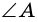
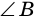
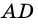
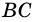
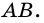
4) Пусть в параллелограмме (рис. 16). Так как то т. е. откуда Но и — внутренние накрест лежащие углы для прямых и и секущей Поэтому

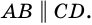
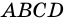
по признаку параллельности прямых). Аналогично доказываем, что Следовательно, — параллелограмм.

Пример:

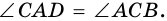
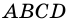
В четырехугольнике Докажите, что — параллелограмм.

Доказательство:

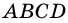
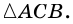
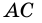
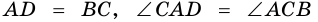
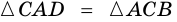
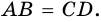
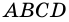
Пусть — данный четырехугольник (рис. 22). Рассмотрим и — их общая сторона, (по условию). Тогда, (по двум сторонам и углу между ними). Следовательно, Но тогда в четырехугольнике противолежащие стороны попарно равны, поэтому он является параллелограммом.

О некоторых видах четырехугольников (квадраты, прямоугольники, равнобокие и прямоугольные трапеции) знали еще древнеегипетские и вавилонские математики.

Термин «параллелограмм» греческого происхождения, считают, что он был введен Евклидом (около 300 г. до н. э.). Также известно, что еще раньше о параллелограмме и некоторых его свойствах уже знали ученики школы Пифагора («пифагорейцы»).

В «Началах» Евклида доказана следующая теорема: в параллелограмме противолежащие стороны равны и противолежащие углы равны, а диагональ делит его пополам, но не упоминается о том, что точка пересечения диагоналей параллелограмма делит каждую из них пополам.

Евклид также не упоминает ни о прямоугольнике, ни о ромбе.

Полная теория параллелограммов была разработана лишь в конце Средневековья, а в учебниках она появилась в XVII в. Все теоремы и свойства параллелограмма в этих учебниках основывались на аксиоме параллельности Евклида.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник