Доказать что прямая принадлежит плоскости
Доказать что прямая принадлежит плоскости
Сформулируем условие принадлежности прямой плоскости как аксиомы:
Аксиома 1. Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости.
Аксиома 2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости.
Проиллюстрируем примерами использование этих аксиом.
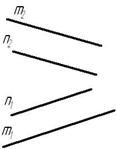
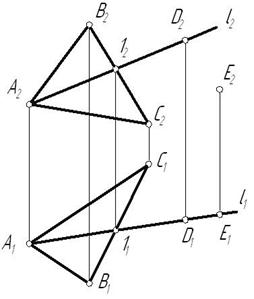
Требуется найти недостающие проекции прямой m, если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k.
Проекция прямой m2 пересекает проекции прямых n2 и k2 в точках В2 и С2 соответственно. Для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек, лежащих на прямых n и k соответственно.
Таким образом, точки В и С принадлежат плоскости, заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит, согласно аксиоме 1, прямая принадлежит этой плоскости.
Рисунок 53. Прямая и плоскость имеют две общие точки
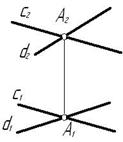
Задача. Через точку В провести прямую m, если известно, что она принадлежит плоскости заданной пересекающимися прямыми n и k (рис. 5 4).
Таким образом, точка В принадлежит плоскости, заданной пересекающимися прямыми n и k, а прямая m проходит через эту точку и параллельна прямой k , значит согласно аксиоме 2 прямая принадлежит этой плоскости.
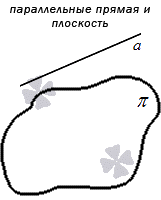
Параллельные прямая и плоскость, признак и условия параллельности прямой и плоскости
Статья рассматривает понятия параллельность прямой и плоскости. Будут рассмотрены основные определения и приведены примеры. Рассмотрим признак параллельности прямой к плоскости с необходимыми и достаточными условиями параллельности, подробно решим примеры заданий.
Параллельные прямые и плоскость – основные сведения
Прямая и плоскость называются параллельными, если не имеют общих точек, то есть не пересекаются.
Параллельность прямой и плоскости – признак и условия параллельности
Не всегда очевидно, что прямая и плоскость параллельны. Зачастую это нужно доказать. Необходимо использовать достаточное условие, которое даст гарантию на параллельность. Такой признак имеет название признака параллельности прямой и плоскости. Предварительно рекомендуется изучить определение параллельных прямых.
Рассмотрим теорему, используемую для установки параллельности прямой с плоскостью.
Если одна из двух параллельных прямых параллельна плоскости, то другая прямая лежит в этой плоскости либо параллельна ей.
Условие применимо, когда необходимо доказать параллельность в прямоугольной системе координат трехмерного пространства. Рассмотрим подробное доказательство.
Значит, перпендикулярность векторов a → и n → очевидна. Отсюда следует, что прямая с плоскостью являются параллельными.
Ответ: прямая с плоскостью параллельны.
Отсюда следует, что прямая А В с координатной плоскостью О y z не являются параллельными.
Ответ: не параллельны.
Из определения следует, что прямая a с плоскостью α не должна иметь общих точек, то есть не пересекаться, только в этом случае они будут считаться параллельными. Значит, система координат О х у z не должна иметь точек, принадлежащих ей и удовлетворяющих всем уравнениям:
Система уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 не имеет решения, когда ранг основной матрицы меньше ранга расширенной. Это проверяется теоремой Кронекера-Капелли для решения линейных уравнений. Можно применять метод Гаусса для определения ее несовместимости.
Для решения данного примера следует переходить от канонического уравнения прямой к виду уравнения двух пересекающихся плоскостей. Запишем это так:
Видим, что она не решаема, значит прибегнем к методу Гаусса.
Отсюда делаем вывод, что система уравнений является несовместной, так как прямая и плоскость не пересекаются, то есть не имеют общих точек.
Ответ: прямая и плоскость параллельны.
Доказать что прямая принадлежит плоскости
Контрольные задания по теме:
Рабочая тетрадь задача 39, задача 40а, задача 40б
Точка принадлежит прямой, если её проекции лежат на одноимённых проекциях этой прямой (рис. 21а).
Точка принадлежит плоскости, если она лежит на прямой, лежащей в этой плоскости (рис.21б).
Прямая принадлежит плоскости, если она проходит через две точки, лежащие в этой плоскости (рис.21в).
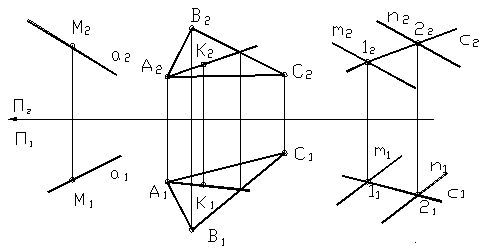
Рисунок 21
Прямая параллельна плоскости, если она параллельна любой прямой, лежащей в этой плоскости. На рисунке 22 изображена прямая t, параллельная прямой b, принадлежащей плоскости Σ: t // b Î Σ (a Ç b).
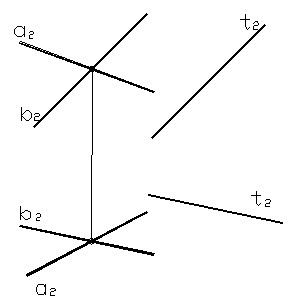
Рисунок 22
Через любую точку пространства можно провести бесконечное множество прямых, параллельных данной плоскости.
Это задача на определение общей точки прямой и плоскости. Её называют также точкой встречи. Рассмотрим пересечение прямой с плоскостью частного положения.
Плоскость Σ задана треугольником АВС и является горизонтально проецирующей плоскостью. Точка встречи прямой k с плоскостью Σ определяется по горизонтальной проекции. Фронтальная проекция точки К достраивается с помощью линии связи. Символическая запись будет выглядеть следующим образом: k Ç Σ (ABC) = K.
Видимость прямой относительно плоскости определяется при помощи фронтально-конкурирующих точек 1 и 2.
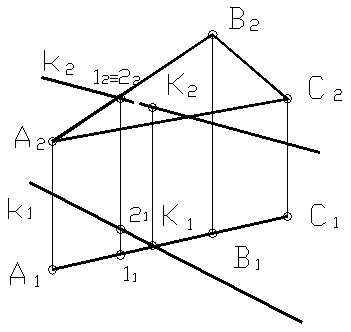
Рисунок 23
Пересечение прямой с плоскостью общего положения изображено на рисунке 24. В этом случае нужно заключить прямую в проецирующую плоскость.
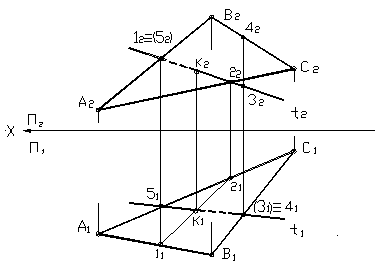
Рисунок 24
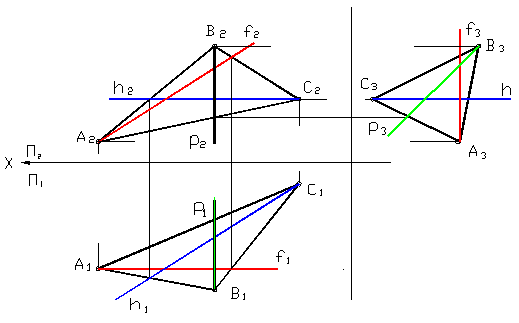
Рисунок 25
1. Сформулируйте условия принадлежности точки плоскости и прямой плоскости.
2. Как построить прямую параллельную заданной плоскости?
3. Вспомните этапы решения задачи на определение точки пересечения прямой и плоскости.
4. Какие точки называются конкурирующими?
5. Как провести в плоскости горизонталь и фронталь?
6. Какие еще особые прямые плоскости вы знаете?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Принадлежность прямой и точки плоскости



Рис. 3.2 Взаимное расположение прямых
Прямые в пространстве могут занимать относительно друг друга одно из трех положений:
1) быть параллельными;
Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.
Если прямые параллельны друг другу, то на КЧ их одноименные проекции тоже параллельны (см. п. 1.2).
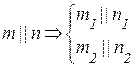
Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.
У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А. Причем фронтальная (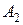
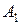
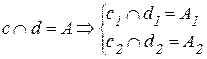
Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.
Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.
На рис. 3.4 точка С принадлежит прямой b, а точка D – прямой а. Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций. Аналогично точки E и F принадлежат разным прямым, но находятся на одном расстоянии от горизонтальной плоскости проекций. Поэтому на КЧ их фронтальные проекции совпадают.
Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.5).
Признак принадлежности точки и прямой плоскости:
Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости.
Прямая принадлежит плоскости, если имеет с ней две общие точки или имеет с ней одну общую точку и параллельна другой прямой, лежащей в этой плоскости.
На рис. 3.5 изображена плоскость 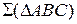
На рис. 3.6 показана плоскость 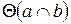
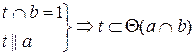
Прямая принадлежит плоскости, если



— она проходит через две точки, принадлежащие плоскости;
— она проходит через точку, принадлежащую плоскости, и параллельна другой прямой, лежащей в этой плоскости или параллельной ей.

Основываясь на признаке принадлежности точки плоскости, через точку М следует провести произвольную прямую, лежащую в плоскости АВС. Поскольку точка М принадлежит вводимой прямой, то горизонтальная проекция этой прямой должна проходить через горизонтальную проекцию точки М. Так как эта прямая принадлежит заданной плоскости, то со сторонами угла АВС она должна пересекаться, и точки 1 и 2 – горизонтальные проекции точек пересечения. Определив фронтальные проекции 1′ и 2′ можно найти фронтальную проекцию прямой, проведенной через точку М. Искомая проекция m’ находится на фронтальной проекции 1’2′ в проекционной связи с m.
Из бесконечного множества прямых, принадлежащих плоскостям, выделяют семейства прямых, расположенных некоторым особенным образом относительно плоскостей проекций (рис. 1.16 а).
Прямые, принадлежащие плоскости и параллельные горизонтальной плоскости проекций, называют горизонталями плоскости.
Прямые, принадлежащие плоскости и параллельные фронтальной плоскости проекций, называют фронталями плоскости.
Если в плоскости, заданной параллельными прямыми АВ и CD (рис. 1.16 б), необходимо построить произвольную горизонталь, то начинать следует с проведения фронтальной проекции горизонтали параллельно оси x, поскольку горизонталь – это прямая, параллельная плоскости H. Но в то же время горизонталь – прямая, принадлежащая плоскости, поэтому с прямыми АB и CD она должна пересекаться, и точки 1′ и 2′ – фронтальные проекции точек пересечения. Горизонтальные проекции 1 и 2 точек пересечения располагаются на горизонтальных проекциях ab и cd соответствующих прямых. Соединив точки 1 и 2 прямой, получим горизонтальную проекцию горизонтали.
Если необходимо построить проекции произвольной фронтали, принадлежащей плоскости, заданной параллельными прямыми АВ и CD, то построения следует начинать с горизонтальной проекции. Поскольку фронталь – прямая, параллельная фронтальной плоскости проекций, то ее горизонтальная проекция должна быть параллельна оси x. При этом фронталь – прямая, принадлежащая плоскости, и с прямыми AB и CD она должна пересекаться. Тогда точки 3 и 4 (рис. 1.16 б) – горизонтальные проекции точек пересечения фронтали с соответствующими прямыми. Построив фронтальные проекции 3′ и 4′ точек пересечения и соединив их прямой, получим фронтальную проекцию фронтали.
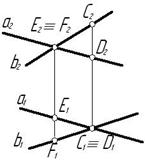
Все горизонтали плоскости параллельны между собой (см. рис. 1.16 а), и одной из них является горизонтальный след плоскости. Аналогично, все фронтали плоскости параллельны между собой, и одной из них является фронтальный след плоскости. Поэтому, если необходимо построить горизонталь и фронталь в плоскости, заданной следами (рис. 1.17), то направление этих прямых уже известно, и для их построения достаточно лишь одной точки, принадлежащей плоскости. Для построения проекций горизонтали на рис.1.17 использованы проекции точки В, а для построения проекций горизонтали – проекции точки А. Точка С – точка пересечения горизонтали и фронтали.
Положение плоскости относительно плоскостей проекций
По положению относительно плоскостей проекций плоскости различают плоскости общего и частного положения.
Плоскости не перпендикулярные ни к одной из плоскостей проекций называют плоскостями общего положения.
Плоскости перпендикулярные к одной или двум плоскостям проекций называют плоскостями частного положения.
В таблице 1.2 приведены наглядные изображения и чертежи заданных треугольниками плоскостей, расположенных относительно плоскостей проекций всеми возможными вариантами. В системе трех взаимно перпендикулярных плоскостей проекций существуют три семейства плоскостей, перпендикулярных к одной и только одной плоскости проекций – варианты 2, 3 и 4.
Если же плоскость перпендикулярна к двум плоскостям проекций, то она перпендикулярна к линии пересечения плоскостей проекций, т.е. к одной из осей. Ось перпендикулярна к третьей плоскости проекций. Следовательно, плоскость, перпендикулярная к двум плоскостям проекций, параллельна третьей плоскости проекций. Таким образом, существует еще три семейства плоскостей, параллельных плоскостям проекций – варианты 5, 6 и 7.
Положение плоскости относительно плоскостей проекций
| № варианта | Положение плоскости относительно плоскостей проекций | Наглядное изображение | Изображение на чертеже |
| Плоскость не перпендикулярна ни к одной из плоскостей проекций (плоскость общего положения) |  |  | |
| Плоскость перпендикулярна к одной из плоскостей проекций | Плоскость перпендикулярна к горизонтальной плоскости проекций (горизонтально-проецирующая плоскость) |  |  |
| Плоскость перпендикулярна к фронтальной плоскости проекций (фронтально-проецирующая плоскость) |  |  | |
| Плоскость перпендикулярна к профильной плоскости проекций (профильно-проецирующая плоскость) |  |  |
Продолжение таблицы 1.2
| Плоскость перпендикулярна к двум плоскостям проекций | Плоскость параллельна горизонтальной плоскости проекций (горизонтальная плоскость) | 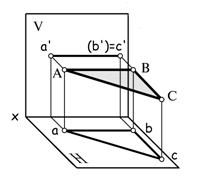 |  |
| Плоскость параллельна фронтальной плоскости проекций (фронтальная плоскость) | 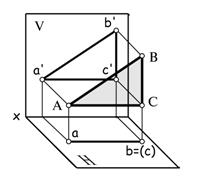 |  | |
| Плоскость параллельна профильной плоскости проекций (профильная плоскость) | 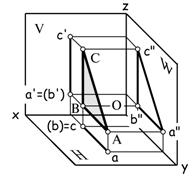 |  |
Плоскость, перпендикулярная к некоторой плоскости проекций, проецируются на нее в виде прямой – см. варианты 2 – 7. Если в этой плоскости лежит точка, прямая или любая плоская фигура, то их проекции совпадают с прямой линией, в которую проецируется вся плоскость.
Пересечение прямой линии с проецирующей плоскостью.
Пусть необходимо построить проекции точки пересечения прямой DE (рис. 1.18) с плоскостью, заданной треугольником АВС. Прямая DE – прямая общего положения, а плоскость АВС, судя по ее фронтальной проекции, – фронтально-проецирующая плоскость.

При необходимости решение подобных задач заканчивается определением видимости рассматриваемых фигур на различных плоскостях проекций. Будем полагать, что прямая DE бесконечна, а плоскость непрозрачна и ограничена треугольником АВС. Из-за того, что заданная плоскость перпендикулярна к фронтальной плоскости проекций, плоскость АВС не закрывает на плоскости V ни одной из точек прямой DE, за исключением самой точки М.
При определении видимости прямой в данной задаче из-за простоты ее условий (заданная плоскость является проецирующей) можно воспользоваться более простой процедурой. Очевидно, что на горизонтальной плоскости проекций будет видна та часть прямой, которая располагается выше плоскости АВС, а та часть прямой, которая находится ниже заданной плоскости, видна не будет. Если обратиться к фронтальной проекции прямой и плоскости, то можно убедиться, что выше плоскости АВС располагается луч МЕ, а луч MD находится ниже заданной плоскости.
Пересечение двух плоскостей,
одна из которых является проецирующей
Пусть имеются две плоскости (рис. 1.19), одна из которых задана треугольником АВС, а другая – треугольником DEF. Требуется построить проекции прямой, по которой эти плоскости пересекаются.
Проекции треугольника АВС также представляют собой треугольники, следовательно, плоскость АВС – плоскость общего положения. Плоскость, треугольника DEF, судя по его фронтальной проекции, является фронтально-проецирующей.

Если считать, что треугольники лишь задают положение плоскостей, то прямую, по которой плоскости пересекаются, следует считать бесконечной. Если же в данной задаче рассматривать пересечение двух непрозрачных пластин в форме треугольников, то прямую, по которой эти пластины пересекаются, следует ограничить отрезком, который может существовать на участке, где имеется и треугольник АВС, и треугольник DEF. Поэтому прямую пересечения двух плоскостей следует ограничить отрезком МN2, где точка N2 – точка пересечения прямой EF с плоскостью АВС.
Пересечение прямой линии с плоскостью общего положения
Если необходимо построить проекции точки пересечения прямой с плоскостью общего положения, например, прямой АВ с плоскостью Р (рис. 1.20), то следует поступить следующим образом.
1. Заключить прямую в плоскость:
2. Построить прямую, по которой вспомогательная плоскость пересекается с заданной:
3. Найти точку пересечения построенной прямой с заданной прямой:
Прямая КL – прямая, по которой пересекается заданная плоскость Р со вспомогательной плоскостью Т – является общей для плоскостей Р и Т. Заданная прямая АВ и прямая KL пересекаются, т.к. лежат в одной и той же плоскости Т. При этом точка М пересечения этих прямых будет принадлежать как прямой АВ, так и плоскости Р, поскольку является одной из точек прямой KL, принадлежащей плоскости Р.
Рассмотрим реализацию изложенного плана решения подобной задачи на чертеже.
Пусть заданы прямая АВ (рис. 1.21) и плоскость треугольника CDE. Требуется построить проекции точки пересечения прямой и плоскости.

Построение проекций линии пересечения двух плоскостей
общего положения
Для построения прямой, по которой пересекаются две плоскости (рис. 1.22), например, плоскость Q, заданная параллельными прямыми АВ и СD, и плоскость Р, заданная треугольником DEF, как правило, необходимо располагать двумя точками, принадлежащими как одной плоскости, так и другой плоскости – точками общими для двух пересекающихся плоскостей. Одним из способов построения таких точек является определение точек пересечения прямых, принадлежащих одной из плоскостей, с другой плоскостью. Например, можно выяснить положение точки М, в которой прямая АВ пересекает плоскость Р, и положение точки N пересечения прямой CD с плоскостью Р. Полученные точки соединить прямой линией.
Рассмотрим реализацию этого пространственного плана на чертеже, где одна из плоскостей задана треугольником EFG (рис. 1.23), а другая – параллельными прямыми AB и CD. Требуется построить проекции прямой, по которой эти плоскости пересекаются.

1.6. Способы преобразования чертежа
Из рассмотрения особенностей проецирования прямых и плоскостей, находящихся в общем и частном положении относительно плоскостей проекций, а также приемов решения задач, в которых присутствуют эти геометрические объекты, следует сделать вывод, что частное положение прямых или плоскостей является предпочтительным. Например, отрезки прямой, параллельной какой-либо плоскости проекций, проецируются на нее в натуральную величину, можно определить углы наклона прямой к плоскостям проекций. Если плоскость занимает проецирующее положение, то легко определяются точки пересечения прямой с этой плоскостью, линия пересечения двух плоскостей, углы наклона плоскости к плоскостям проекций.
Общей целью способов преобразования чертежа является переход от общего положения геометрического объекта – к частному, необходимому для решения геометрических задач.
Количество способов преобразования чертежа достаточно велико. Здесь рассматриваются лишь два из них.
Существо одного из способов преобразования состоит в том, что частное положение геометрического объекта относительно некоторой системы плоскостей проекций достигается изменением системы плоскостей проекций, при этом сам геометрический объект остается в пространстве неподвижным. Такой прием носит название способа перемены плоскостей проекций.
Суть другого способа преобразования состоит в том, что частное положение геометрического объекта достигается изменением положения этого объекта путем вращения в неизменной (существующей) системе плоскостей проекций. Такой способ преобразования носит название способа вращения.
Способ перемены плоскостей проекций
Способ перемены плоскостей проекций может осуществляться только при двух обязательных условиях:
а) преобразования чертежа должны обладать непрерывностью, т.е. каждая последующая система плоскостей проекций должна быть связана с предыдущей.
б) геометрический объект при всех преобразованиях должен находиться в системе двух взаимно перпендикулярных плоскостей проекций;
Эти два условия с необходимостью приводят к выполнению следующего правила: при изменении системы двух взаимно перпендикулярных плоскостей проекций можно заменять только одну из плоскостей, оставляя другую плоскость проекций неизменной, при этом новая плоскость должна вводиться перпендикулярно к остающейся.
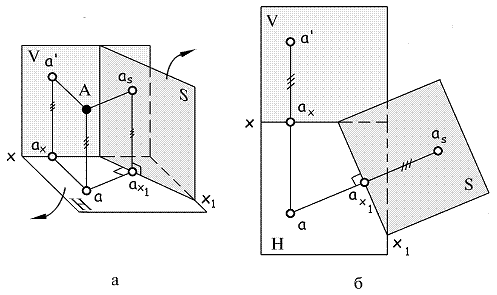
Пусть в системе V,H (рис. 1.24 а) заданы проекции точки А, и по каким-то причинам необходимо ввести новую плоскость S, вместо плоскости V. Плоскость S следует ввести перпендикулярно к плоскости Н, образовав таким образом новую систему двух взаимно перпендикулярных плоскостей проекций – систему H,S. Выполненные действия можно коротко записать в такой форме: V,H Þ H,S; S^H. Для того, чтобы получить проекцию точки А на плоскость S, необходимо осуществить ортогональное проецирование: из точки А провести проецирующий луч перпендикулярно к плоскости S, и там, где этот луч пересечет плоскость S, будем иметь проекцию as точки А на плоскость S. Проекции as и a точки А в системе H,S будут связаны между собой теми же закономерностями, что и проекции a’ и a в системе V,H, в частности, проекции as и a располагаются на прямых перпендикулярных к новой оси x1 и пересекающих ее в одной и той же точке ax1. Отрезок asax1, показывающий удаление точки А от плоскости Н, равен отрезку a’ax (çasax1ç= ça’axç).
Для того, чтобы получить чертеж (плоское изображение), необходимо плоскости H и S совместить с плоскостью V (рис. 1.24 б). Плоскость Н (вместе с плоскостью S) следует повернуть вокруг оси x, опуская переднюю полуплоскость, а затем повернуть плоскость S вокруг оси x1, как показано на рисунке. При этом отрезки aax1 и ax1as образуют линию связи, перпендикулярную к новой оси x1.
На рис. 1.25 показан чертеж при осуществлении перемены плоскостей. Обычно выбор новой системы плоскостей проекций производят, исходя из условий решаемой задачи. Для демонстрации необходимых построений на рис. 1.25 этот выбор сделан произвольно.
Пусть заданы проекции a и a’ точки в системе V,H, и требуется перейти к новой системе плоскостей проекций H,S (и, следовательно, построить недостающую проекцию точки А в новой системе).
Для этого на чертеже проводят новую ось H/S (ось x1), из точки a перпендикулярно к новой оси строят линию связи и от точки ax1 ее пересечения с осью H/S откладывают отрезок равный axa’ (ça’axç=çax1asç) Получают проекцию as точки А на плоскость S.
Если требуется провести замену плоскостей проекций, и перейти от системы V,H к системе V,T, введя Т^V, то на чертеже проводят новую ось V/T (ось x2), из точки a’ перпендикулярно к новой оси строят линию связи, и от точки ax2 ее пересечения с осью V/T откладывают отрезок равный axa (çaaxç=çax2atç). Получают проекцию at точки А на плоскость Т.
Для того, чтобы не ошибаться при построении новых проекций точек, целесообразно запомнить: при построении проекций точек на вводимую плоскость всегда откладывают отрезки линий связей с той плоскости, которую заменяют.
Рассмотрим применение способа перемены плоскостей проекций для решения некоторых задач.

Отрезок АВ и угол наклона прямой к одной из плоскостей проекций будут проецироваться без искажения, если в новой системе плоскостей проекций заданная прямая окажется в частном положении – будет параллельна новой плоскости проекций. Поэтому от существующей системы плоскостей проекций V,H перейдем к новой системе V,T, введя плоскость Т^V и T||АВ. При этом новая ось V/T должна быть проведена параллельно a’b’. Построим проекцию atbt отрезка АВ на плоскость Т. Поскольку в системе плоскостей проекций V,T отрезок АВ параллелен плоскости Т, то на плоскость Т он проецируется в натуральную величину, а угол b между atbt и осью V/T равен углу наклона отрезка АВ к плоскости V.
Для определения натуральной величины отрезка и угла его наклона к плоскости Н следует перейти от существующей системы плоскостей проекций V,H к новой системе H,S, введя плоскость S^H и S||AB. Проведем H/S çç ab и построим проекцию asbs отрезка АВ на плоскость S. В системе плоскостей проекций H,S отрезок АВ параллелен плоскости S, поэтому отрезок проецируется на плоскость S без искажения, а угол a наклона asbs к оси H/S равен углу наклона прямой к плоскости Н.
Иногда для решения задачи требуется, чтобы прямая оказалась в новой системе плоскостей проекций проецирующей – перпендикулярной к одной из новых плоскостей проекций. Следует помнить, что при всех заменах необходимо соблюдать сформулированное ранее требование взаимной перпендикулярности плоскостей проекций, образующих новую систему, и потому новая плоскость должна быть введена перпендикулярно к остающейся (должна быть проецирующей в существующей системе плоскостей проекций). Если задана прямая общего положения, то ввести сразу плоскость, перпендикулярную к прямой, не представляется возможным: новая плоскость в существующей системе плоскостей проекций также будет занимать общее положение. Для того, чтобы такая замена стала возможной, заданная прямая должна быть параллельна некоторой плоскости проекций. Тогда плоскость, перпендикулярная к прямой, будет перпендикулярна и к остающейся плоскости проекций.
Если необходимо, чтобы прямая АВ (рис. 1.26) в новой системе плоскостей проекций заняла проецирующее положение, то следует воспользоваться ситуацией, создавшейся после перехода от системы V,H к системе H,S. Прямая АВ параллельна плоскости S, и, если ввести плоскость Q перпендикулярную к АВ, то эта плоскость будет перпендикулярна и к плоскости S – образовывать с ней новую систему S,Q двух взаимно перпендикулярных плоскостей проекций. Для построения проекции АВ на плоскость Q следует провести линию связи перпендикулярно к оси S/Q. От точки пересечения с осью отложить отрезки линий связи с заменяемой плоскости, т.е. с плоскости Н. При этой замене «старой» будет система H,S, поэтому для построения проекций aqbq следует брать отрезки линий связи от точек a и b до оси H/S.
Пусть требуется определить натуральную величину треугольника АВС (рис. 1.27).

Если плоскость фигуры занимает общее положение, то введение при первой же замене плоскости проекций, параллельной плоскости фигуры, оказывается невозможным: новая плоскость в системе V,H также будет занимать общее положение, чем нарушается одно из обязательных условий данного способа преобразования. Введение необходимой плоскости станет возможным, если плоскость треугольника в некоторой системе плоскостей проекций станет проецирующей. Такое взаимное положение плоскости фигуры и плоскости проекций должно отвечать признаку перпендикулярности двух плоскостей – плоскости взаимно перпендикулярны, если одна из них содержит прямую, перпендикулярную к другой плоскости. Конечно, можно выбрать любую прямую, принадлежащую плоскости фигуры, и путем замены плоскостей проекций добиться того, чтобы прямая стала перпендикулярной к некоторой плоскости проекций. Тогда и заданная плоскость займет проецирующее положение. Однако, как показывает предыдущий пример (см. рис. 1.26), только для приведения прямой общего положение в проецирующее положение потребуется две замены плоскостей проекций. Количество преобразований можно сократить, если в плоскости фигуры выбирать не любые прямые, а прямые параллельные плоскостям проекций, т.е. горизонтали или фронтали заданной плоскости.
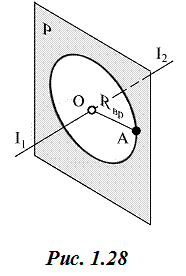
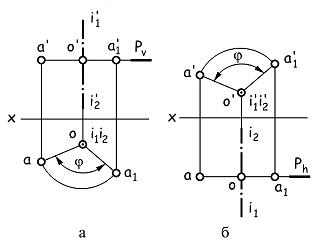
Если точка А (рис. 1.28) вращается вокруг неподвижной прямой I1I2 (оси вращения), то точка описывает окружность, плоскость Р которой (плоскость вращения) перпендикулярна к оси вращения. Центром О этой окружности (центром вращения) является точка пересечения оси вращения с плоскостью вращения, а радиус Rвр окружности (радиус вращения) равен расстоянию от точки А до центра вращения О.
Если ось вращения перпендикулярна к какой-либо плоскости проекций, то плоскость вращения точки параллельна этой плоскости проекций, и окружность, которую описывает точка, проецируется на нее без искажения.
Пусть в системе V,H (рис. 1.29 а) заданы проекции точки А, и требуется повернуть ее вокруг оси I1I2 на некоторый угол j.
Поскольку ось I1I2 перпендикулярна к плоскости Н, то плоскость Р вращения точки А, перпендикулярная к оси вращения, будет расположена параллельно горизонтальной плоскости проекций. Поэтому окружность, описываемая точкой А при вращении, проецируется на плоскость Н без искажения, и радиус вращения равен расстоянию oa. После поворота точки А на угол j (против часовой стрелки на плоскости Н) горизонтальная проекция a точки переместится в положение a1. Вращение точки осуществляется в горизонтальной плоскости Р, поэтому фронтальная проекция a’ перемещается по фронтальному следу Pv и проекции a1 будет соответствовать проекция a1’.
Обсудим, какие изменения произойдут на чертеже, если точку А (рис. 1.29 б) необходимо повернуть на некоторый угол j вокруг оси I1I2, перпендикулярной к фронтальной плоскости проекций.
Поскольку плоскость вращения Р перпендикулярна к оси вращения, то перемещение точки будет осуществляться в плоскости, параллельной фронтальной плоскости проекций – во фронтальной плоскости. Поэтому окружность, по которой перемещается точка А, проецируется на плоскость V без искажения, и радиус вращения точки равен отрезку o’a’. Если повернуть точку А на угол j, то ее фронтальная проекция a’ переместится в положение a1’. При этом горизонтальная проекция точки двигается по горизонтальному следу Рh плоскости вращения, и положению точки после поворота соответствует ее горизонтальная проекция a1.
Способом вращения удобно пользоваться для определения натуральной величины отрезка и углов наклона прямой к плоскостям проекций. Отрезок спроецируется без искажения, если в результате перемещения он станет параллельным какой-либо из плоскостей проекций. При этом вращение отрезка должно осуществляться таким образом, чтобы угол наклона прямой к одной из плоскостей проекций не изменялся. Последнее требование вынуждает вращать отрезок вокруг осей перпендикулярных к плоскостям проекций.
Пусть, например, требуется определить натуральную величину отрезка АВ (рис. 1.30 а) и угол его наклона к горизонтальной плоскости проекций.
Для того чтобы угол наклона прямой к плоскости Н не изменялся, вращение должно осуществляться вокруг оси, перпендикулярной к горизонтальной плоскости проекций, а для того, чтобы отрезок проецировался без искажения, он должен стать параллельным фронтальной плоскости проекций. Сокращая количество построений, проведем ось I1I2 через один из концов отрезка – через точку А. Тогда точка А, находящаяся на оси вращения, при повороте останется неподвижной, а все остальные точки отрезка будут описывать окружности, лежащие в горизонтальных плоскостях и потому проецирующиеся на плоскость Н без искажения. В частности, радиус вращения точки В, перемещающейся в плоскости Р, будет равен ab. При повороте отрезка АВ в положение, параллельное плоскости V, его горизонтальная проекция повернется из положения ab в положение ab1 (параллельное оси x или перпендикулярное к линии связи), которому будет соответствовать фронтальная проекция a’b1’. Частное положение отрезка в системе V,H позволяет утверждать, что величина проекции a’b1’ равна величине отрезка АВ, а угол a есть угол наклона прямой к плоскости Н.
Если требуется определить натуральную величину отрезка АВ (рис. 1.30 б) и угол его наклона к фронтальной плоскости проекций, то вращение отрезка следует осуществлять вокруг оси, перпендикулярной к плоскости V. При проведении оси вращения I1I2 через точку А последняя останется неподвижной, а точка В будет перемещаться во фронтальной плоскости Р, и окружность, по которой происходит это перемещение, проецируется на плоскость V без искажения. После поворота отрезка АВ в горизонтальное положение фронтальная проекция отрезка повернется из положения a’b’ в положение a’b1’ (параллельное оси x или перпендикулярное к линии связи), которому соответствует горизонтальная проекция ab1. Вследствие частного положения отрезка в системе V,H проекция ab1 равна величине отрезка АВ, а угол b есть угол наклона прямой к фронтальной плоскости проекций.
Под многогранниками понимают тела (пространственные фигуры), ограниченные плоскими многоугольниками. Примеры многогранников известны читателю из школьного курса геометрии: призма, пирамида, тетраэдр, гексаэдр (куб) и др.
Плоские фигуры, ограничивающие многогранник, носят наименование граней (рис. 1.31). Прямые, по которым пересекаются смежные грани, называют ребрами, а точки, в которых пересекаются ребра, – вершинами. Фигуру, получающуюся при пересечении многогранника плоскостью, иногда именуют основанием.

Для построения недостающих проекций точек, принадлежащих поверхности многогранника, следует пользоваться теми же соображениями, которые использовались при построении проекций точек на прямых и плоскостях. Например, если задана фронтальная проекция m’ точки М, лежащей на ребре АА1, то горизонтальная проекция m находится в проекционной связи на горизонтальной проекции ребра aa1.
Для построения недостающей фронтальной проекции точки N, принадлежащей грани АА1С1С, (горизонтальная проекция n задана) необходимо основываться на признаке принадлежности точки плоскости. Через точку N следует провести какую-либо прямую, принадлежащую грани АА1С1С, тогда горизонтальная проекция этой прямой могла бы выглядеть как прямая 1-2. По точкам пересечения 1 0 и 2 0 прямой с соответствующими ребрами можно определить ее фронтальную проекцию 1’2′, на которой располагается искомая проекция n’.
Количество построений можно несколько сократить, если при построении недостающей проекции точки проводить через точку прямую, направление которой определено заранее. Пусть, например, задана фронтальная проекция k’ точки K, лежащей на грани ВВ1С1С, и требуется построить горизонтальную проекцию этой точки. Проведем через точку K прямую, параллельную ребру ВВ1.Такая прямая принадлежит грани ВВ1С1С, и потому пересекает ребро ВС. Фронтальная проекция проведенной прямой проходит через точку k’ и параллельна b’b1’. Точка 3′ – фронтальная проекция точки пересечения этой прямой с ребром ВС. Можно построить горизонтальную проекцию 3, а направление горизонтальной проекции проведенной прямой уже известно: она должна быть параллельна bb1. Горизонтальная проекция k находится в проекционной связи на построенной проекции прямой.
Пересечение многогранника с проецирующей плоскостью.
Построение натурального вида фигуры сечения.
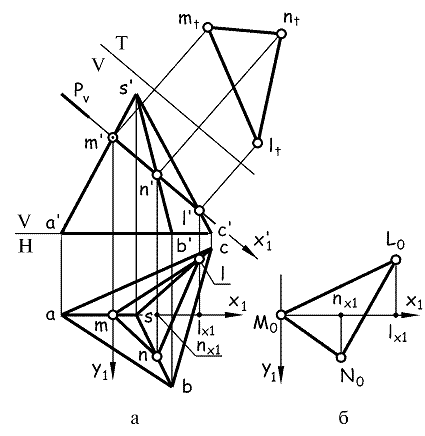
Пусть задана пирамида SABC (рис. 1.33 а), пересеченная фронтально-проецирующей плоскостью Р. Требуется построить проекции и натуральный вид сечения пирамиды плоскостью Р – фигуры, получающейся при пересечении пирамиды плоскостью Р.
Поскольку плоскость Р перпендикулярна к фронтальной плоскости проекций, то фронтальная проекция линии пересечения уже имеется, и остается достроить лишь горизонтальную проекцию искомой линии. При пересечении должен получиться многоугольник, т.к. плоскость Р пересекает грани многогранника по некоторым отрезкам прямых. Вершинами многоугольника (в данном случае треугольника) будут являться точки пересечения плоскости Р с ребрами многогранника. Обозначив фронтальные проекции m’, n’, l’ точек пересечения, найдя их горизонтальные проекции m, n, l и соединив их прямыми, получим горизонтальную проекцию линии пересечения плоскости Р с пирамидой SABC.
Конечно, треугольник MNL ни на фронтальной, ни на горизонтальной плоскостях проекций не проецируется в натуральную величину, поскольку плоскость треугольника не параллельна ни одной из плоскостей проекций. Для определения его истинных размеров можно воспользоваться двумя приемами.
Один из них – способ перемены плоскостей проекций. Зададимся положением пирамиды относительно системы плоскостей проекций V,H – поставим, например, пирамиду на плоскость Н, и перейдем к осному чертежу. Для того, чтобы треугольник MNL проецировался без искажений, следует ввести плоскость Т параллельную плоскости треугольника (и перпендикулярную к плоскости V), и перейти от системы V,H к системе V,T. Проекция треугольника на плоскость Т – mtntlt – будет соответствовать истинным размерам треугольника MNL.
Другой прием – построение натурального вида сечения координатным способом. Необходимо построить плоскую фигуру, а положение любой точки на плоскости определяется двумя координатами. Поэтому можно задаться двумя взаимно перпендикулярными координатными осями, и построить сечение в этой системе координатных осей. При этом направление осей должно быть выбрано таким образом, чтобы размеры вдоль выбранных осей на одну из плоскостей проекций проецировались бы без искажения.
Для удобства построения зададимся началом координат в точке М (рис. 1.33 а). Одну из осей – ось Мх1 – направим в плоскости Р параллельно фронтальной плоскости проекций. Фронтальная проекция этой оси – m’x1’, горизонтальная – mx1. Вторую ось Му1 следует направить в плоскости Р перпендикулярно к оси Мх1 и перпендикулярно к плоскости V. Это будет фронтально-проецирующая прямая, направление которой совпадает с направлением оси Оу. На фронтальную плоскость проекций ось Му1 проецируется в точку, совпадающую с m’, а на горизонтальную – в прямую my1. Поскольку ось Мх1||V, то размеры вдоль оси Мх1 проецируются без искажения на плоскость V, а т.к. ось Му1||Н, то размеры вдоль оси Му1 без искажения проецируются на плоскость Н.
Теперь в любом свободном месте поля чертежа можно провести две взаимно перпендикулярные оси М0x1 и М0y1 (рис. 1.33 б), и построить точки N0 и L0 (точка М0 совпадает с началом принятой системы координат). Размеры вдоль оси М0х1 следует брать с фронтальной проекции: для точки N0 – расстояние m’n’, для точки L0 – m’l’. Размеры вдоль оси М0y1 надо брать с горизонтальной проекции – удаления точек n и l от проекции оси mx1 (расстояния nnx1 и llx1).
Пересечение прямой линии с поверхностью многогранника
Для построения точек пересечения прямой (АВ) с поверхностью многогранника (Мн) необходимо последовательно выполнить следующие действия.
1. Заключить прямую в плоскость: (АВ) Ì Т.
3. Определить точки пересечения построенной ломаной с заданной прямой l 0 Ç (АВ) = Мi.
Пусть задана пирамида SABC (рис. 1.34) и прямая DE. Требуется построить проекции точек пересечения прямой с поверхностью пирамиды.
Взаимное пересечение многогранников
При построении проекций линий взаимного пересечения многогранников используют два приема. Согласно одному из них строят проекции отрезков, по которым грани одного многогранника пересекают грани другого многогранника, т.е., по существу, несколько раз решают задачу на построение проекций линии пересечения плоскостей. Другой прием состоит в том, что находят проекции точек, в которых ребра одного многогранника пересекают грани другого многогранника, а ребра второго многогранника – грани первого, т.е. многократно решают задачу на построение проекций точек пересечения прямой с плоскостью. Покажем использование обоих способов на примере решения конкретной задачи.
Пусть заданы проекции пирамиды SABC (рис. 1.35) и фронтальная проекция призмы, ограничивающей сквозной проем в пирамиде. Грани призматического отверстия перпендикулярны к фронтальной плоскости проекций. Требуется построить проекции лини пересечения пирамиды и призмы.
Горизонтальная проекция 5 построена из соображений принадлежности точки 5 0 грани SAB. Через точку 5 0 проведена горизонталь этой грани, по точке 9 0 пересечения горизонтали с ребром SA построены горизонтальная проекция горизонтали, на которой располагается горизонтальная проекция 5.
Для построения горизонтальных проекций ребер призмы следует провести прямые 1-11, 3-31 и 5-51, соблюдая условия видимости.
Располагая фронтальной и горизонтальной проекциями каждой точки линии пересечения призмы и пирамиды, можно построить профильную проекцию линии пересечения заданных многогранников.
1.8. Кривые линии и поверхности
Существует несколько представлений о кривой линии как геометрической фигуре. Одно из них базируется на кинематической модели, согласно которой кривая линия есть траектория (все последовательные положения) перемещающейся точки.
Если перемещение точки происходит в одной и той же плоскости, то траектории движения точки представляют собой плоские кривые (эллипс, парабола, синусоида и др.). Во всех других случаях образуются пространственные кривые, примерами которых могут служить цилиндрические и конические винтовые линии.
Если движение точки подчиняется определенному закону, то траектория ее движения представляет собой закономерную кривую. В противном случае кривые называют незакономерными или случайными. Если закономерные кривые могут быть описаны алгебраическими уравнениями, то такие кривые называют алгебраическими: окружность, гипербола и др.
Возьмем на кривой точку К и несовпадающую с ней точку М1. Проведя прямую КМ1, получим некоторую секущую. Если точку К оставить неподвижной, а точку М начать перемещать по кривой в сторону точки К, то положение секущей начнет изменяться: из положения КМ1 она перейдет в положение КМ2, и при дальнейшем приближении точки М к точке К секущая будет изменять свое положение, вращаясь вокруг точки К. Предельное положение секущей, при котором точка М совпадет с точкой К, называется касательной к кривой в данной точке. Следует отметить, что проекция kplp касательной KL к пространственной кривой является в общем случае касательной к проекции кривой.
Одним из возможных представлений о криволинейной поверхности является кинематическая модель, согласно которой поверхность рассматривается как все последовательные положения движущейся в пространстве линии.
Если движение линии происходит по какому-либо закону, то возникающую поверхность рассматривают как закономерную, в противном случае поверхность считают незакономерной или случайной. Поверхности, которые могут быть описаны алгебраическим уравнением, называют алгебраическими. Примерами алгебраических поверхностей могут служить поверхности цилиндра, конуса, сферы и др.
Линию (l 0 ), производящую поверхность в каждом своем положении, называют образующей.
Линию (t 0 ), задающую закон перемещения образующей, называют направляющей.
Поверхности, которые могут быть образованы перемещением прямолинейной образующей, называют линейчатыми. Все другие поверхности называют нелинейчатыми.
Примеры цилиндрических и конических поверхностей
Примерами линейчатых поверхностей являются цилиндрические и конические поверхности.
Цилиндрические поверхности образуются перемещением прямолинейной образующей, во всех своих положениях сохраняющей параллельность некоторой заданной прямой и проходящей через все точки некоторой кривой направляющей линии.
Цилиндрические поверхности различают по виду кривой линии, которая получается при пересечении поверхности плоскостью, перпендикулярной к образующим. Если при таком пересечении получается кривая второго порядка, то и цилиндрическая поверхность относится к числу поверхностей второго порядка. Такой цилиндр может быть параболическим, гиперболическим или эллиптическим.
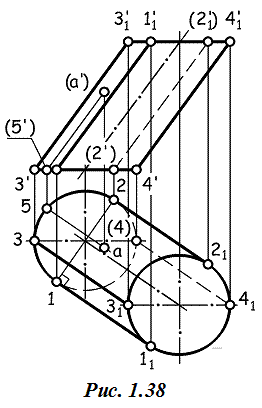
Обратим внимание на проекции образующих, ограничивающих изображение цилиндра на фронтальной и горизонтальной проекциях. Эти образующие ограничивают видимые части цилиндрической поверхности, но не находятся в проекционной связи. На горизонтальной проекции видимая часть поверхности ограничивается образующими 1 0 1 0 1 и 2 0 2 0 1. Для построения фронтальной проекции образующей 1 0 1 0 1 необходимо определить вначале точку касания горизонтальной проекции 1-11 к проекции окружности нижнего основания (для чего из центра окружности надо опустить перпендикуляр на проекцию очерковой образующей), затем найти фронтальную проекцию 1′ и провести прямую 1’1′1 параллельно фронтальным проекциям образующих цилиндрической поверхности. Аналогично выстраиваются проекции образующей 2 0 2 0 1. Для построения горизонтальных проекций образующих 3 0 3 0 1 и 4 0 4 0 1, ограничивающих видимую часть цилиндрической поверхности на фронтальной проекции, следует учесть проекционную связь точек 3′ и 3, 4′ и 4, а также взаимную параллельность всех образующих.
При построении недостающей проекции точки, принадлежащей поверхности, следует руководствоваться признаком принадлежности точки поверхности: точка принадлежит поверхности, если она принадлежит линии, лежащей на поверхности.
Коническая поверхность образуется перемещением прямолинейной образующей, во всех своих положениях проходящей через некоторую неподвижную точку (вершину) и все точки кривой направляющей линии.
Если линия, которая получается при пересечении конической поверхности плоскостью, не проходящей через вершину, является кривой второго порядка (эллипсом, окружностью, параболой, гиперболой), то и коническая поверхность представляет собой поверхность второго порядка. Каждая из названных линий может быть принята в качестве направляющей конической поверхности.

Поскольку сечения конуса плоскостями, параллельными основанию, представляют собой окружности, то для построения недостающей горизонтальной проекции точки можно использовать окружность. Фронтальная проекция окружности, проведенной через точку А, представляет собой отрезок прямой, проходящей через a’ и параллельной проекции основания конуса. Центр О такой окружности располагается на оси конуса, а радиус без искажения проецируется на фронтальной проекции как отрезок от o’ до очерковой образующей. Построив горизонтальную проекцию окружности, можно найти проекцию a.
Поверхности вращения образуются путем вращения какой-либо линии вокруг неподвижной прямой – оси поверхности.