Доказать что равенство ab ba e
Обратная матрица. Квадратная матрица n-го порядка, у которой по диагонали 1, а все остальные элементы 0, называется единичной и обозначается E



Операции с матрицами
Квадратная матрица n-го порядка, у которой по диагонали 1, а все остальные элементы 0, называется единичной и обозначается E.
Для любой матрицы A справедливы равенства AE=EA=A. Таким образом, единичная матрица играет роль 1 среди матриц.
Определение 6.1. Матрица B называется обратной к матрице A, если AB=BA=E. Обратная матрица обозначается 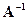
Понятие обратной матрицы существует только для квадратных матриц.
Свойство 6.1. Если обратная матрица существует, то она единственна.
Доказательство проведем методом от противного. Пусть существует две обратные матрицы к A, которые обозначим через B и C. Рассмотрим произведение BAC. С одной стороны (BA)C=EC=C, а с другой B(AC)=BE=B. Результат не зависит от способа расстановок скобок, поэтому B=C.
Определение 6.2. Матрица называется невырожденной, если ее определитель отличен от 0.
Теорема 6.1. Необходимым и достаточным условием существования обратной матрицы к A является ее невырожденность.
Доказательство. Пусть к матрице A существует обратная 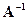
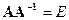
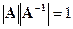
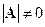
Пусть 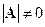
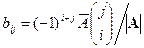
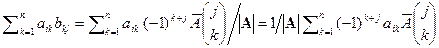
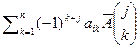
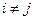
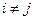
Следствие 6.1 Если BA=E или AB=E, то 
Доказательство. Если BA=E, то матрица A – невырожденная, и к ней существует единственная обратная матрица. Далее, 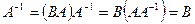
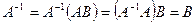
Произведение матриц и его свойства.
2.3.1. Определение. Произведением строки A=(а1, а2, … аn) на столбец B=(b1, b2, … bn) T называется число a1b1+a2b2+…+anbn.
Это произведение обозначается через AB.
AB=(1, 2, 4) 
Таким образом, по определению
(а1, а2, … аn) 
то есть для того, чтобы строку умножить на столбец, необходимо, чтобы число элементов строки равнялось числу элементов столбца.
2.3.2. Определение. Произведением матрицы A=(aij)m´n на матрицу B=(bij)n´k называется матрица C=(cij)m´k, такая, что
Произведение матрицы A на матрицу B обозначается через AB.
Таким образом, AB=(ai1b1j+ai2b2j+…+ainbnj)m´n, то есть элемент cij произведения A на B получается как произведение i—й строки (то есть строки под номером i) матрицы A на j—й столбец (то есть столбца под номером j) матрицы B. В частности, для того, чтобы умножить матрицу A на матрицу B, необходимо, чтобы число элементов в строке матрицы A совпадало с числом элементов в столбцах матрицы B, что означает, что число столбцов первого сомножителя должно совпадать с числом строк второго. В противном случае произведение матриц не существует. При этом число строк произведения AB равно числу строк первой матрицы A, а число столбцов равно числу столбцов второй матрицы B. Так, произведение матрицы A=(aij)2´2 на матрицу B=(bij)2´2 является матрицей C=(cij)2´2 размерности 2´2:






Произведение B=(bij)2´3 на A=(aij)2´2 не существует, так как число 3 столбцов матрицы B не равно числу 2 строк матрицы A. Например, если A= 


AB= 



BA= 



AC= 



CA не определено (то есть не существует).
В частности, мы видим, что, вообще говоря, AB≠BA, то есть привычное для чисел правило «от перестановки мест сомножителей призведение не меняется» для матриц не работает.
2.3.3. Теорема. Операция произведения матриц обладает следующими свойствами:
(AB)C=A(BC).
a(AB)=(aA)B=A(aB).
A(B+C)=AB+AC.
(A+B)C=AC+BC.
2.3.4. Перечисленные свойства естественным образом обобщаются. Например, как и в случае суммы, свойство 2 о обобщается следующим образом:
и результат произведения не зависит от расстановки скобок.
В силу этого в произведениях типа (2.2) скобки принято опускать:
Вообще, в произведении (2.3) определено произведение любого количества l друг за другом идущих матриц: AiAi+1…Ai+l—1. В силу свойства 1 о результат произведения зависит от порядка следования сомножителей. Более того, при перестановке сомножителей произведение может быть вообще не определённым (то есть не существовать).
Здесь сочетания знаков «+» и «-» произвольные.
(A1A2…Ak—1Ak) Т = 
A k = 
Упражнения.
2.4.1. Выполнить действия:
а) 4 



в) 2 


а) A=(2, 3, 4), B=(2, 1, 3) T ; б) A=(2, 3, 4), B= 
в) A= 



д) A= 



Решение. в) AB не определено, так как число 3 столбцов A не совпадает с числом 2 строк B.
BA= 



Ответ: в) AB и B T A T не определены, BA= 

2.4.3. Вычислить:
а) 


Решение. б) 









Замечаем, что 



Ответ: б) 
2.4.4. Вычислить:
а) 


-2 

б) 


+3 

Решение. а) Выполним вычисления по действиям:
1) 



=
2) 


=
3) 6 






= 
5) 2 


6) 


-2 

= 


Ответ: а)






