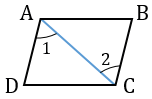
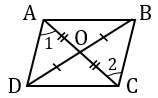
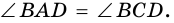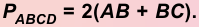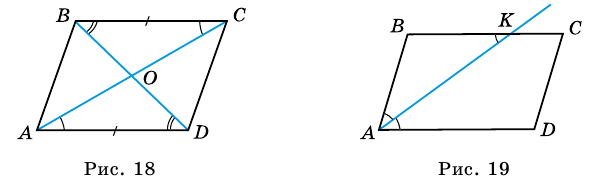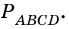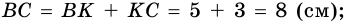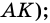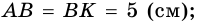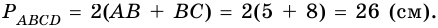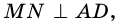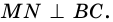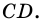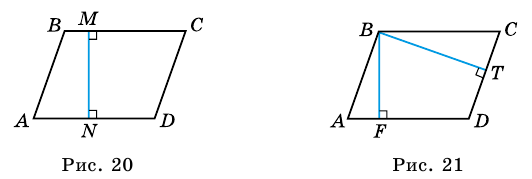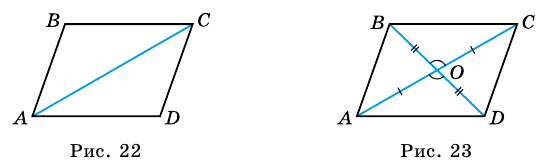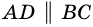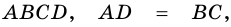Доказать что стороны параллелограмма равны

Признаки параллелограмма

Признаки параллелограмма — это признаки,
с помощью которых можно доказать,
что четырехугольник — параллелограмм.

Чтобы доказать, что четырехугольник — параллелограмм, нужно знать признаки
параллелограмма. Четырехугольник является параллелограммом, если один
из признаков параллелограмма для этого четырехугольника истинен.
Например, если у четырехугольника две стороны равны и
параллельны, значит этот четырехугольник параллелограмм.

Всего существует три признака параллелограмма: по двум одинаковым
параллельным сторонам, по пересечению диагоналей и делению
диагоналей пополам в точке пересечения, по попарно равным
противоположным сторонам. В этой статье мы рассмотрим
все три признака параллелограмма.

I признак параллелограмма

По пересечению диагоналей и делению
диагоналей в точке пересечения пополам.

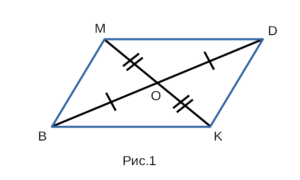
Четырехугольник является параллелограммом, если у четырехугольника
диагонали пересекаются, и в точке пересечения делятся пополам.

Если на рисунке 1 — BO = OD, MO = OK, то BMDK — параллелограмм.

II признак параллелограмма

По двум одинаковым параллельным сторонам.

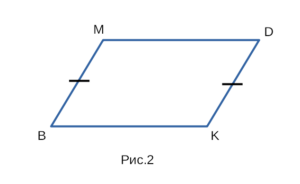
Четырехугольник является параллелограммом, если у четырехугольника
две стороны равны и параллельны.

Если на рисунке 2 — BM = DK, BM || DK, то BMDK — параллелограмм.

III признак параллелограмма

По попарно равным противоположным сторонам.

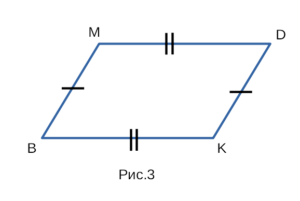
Четырехугольник является параллелограммом, если у
четырехугольника противоположные стороны попарно равны.

Если на рисунке 3 — BM = DK, MD = BK, то BMDK — параллелограмм.

В этой статье мы рассмотрели все три признака параллелограмма и
теперь можем доказать, что некий четырехугольник параллелограмм.

В следующей статье про площадь параллелограмма вы узнакете как её расчитать.

Источник

Признаки параллелограмма

Доказательство:

Дано: АВСD — четырехугольник, АD = ВС, АDВС.

Доказать: АВСD — параллелограмм.

Доказательство:

1. Проведем диагональ АС четырехугольника АВСD.

Доказательство:

Доказать: АВСD — параллелограмм.

Доказательство:

1. Проведем диагональ АС четырехугольника АВСD.

3. Итак, АD = ВC, АDВС, по 1 0 признаку параллелограмма, четырехугольник АВСD — параллелограмм. Что и требовалось доказать.

Доказательство:

Доказать: АВСD — параллелограмм.

Доказательство:

1. Рассмотрим АОD и ВОС: по условию АО = ОС, DО = ОВ, АОD и ВОС (как вертикальные углы), АОD =ВОС (по 1 признаку равенства треугольников), АD = ВC и 1 = 2.

2. 1 и 2 накрест лежащие при пересечении прямых АD и ВC секущей АС, при этом 1 = 2, по признаку параллельности двух прямых АDВС.

3. Итак, АD = ВC, АDВС, по 1 0 признаку параллелограмма, четырехугольник АВСD — параллелограмм. Что и требовалось доказать.

Поделись с друзьями в социальных сетях:

Источник

Параллелограмм, его свойства и признаки с примерами решения

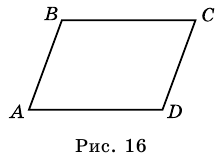
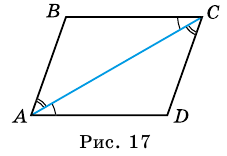
Параллелограммом называют четырехугольник, у которого противолежащие стороны попарно параллельны.

На рисунке 16 изображен параллелограмм

Рассмотрим свойства параллелограмма.

1. Сумма двух любых соседних углов параллелограмма равна 180°.

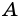
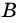
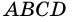
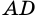
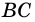
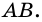
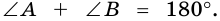
Действительно, углы и параллелограмма (рис. 16) являются внутренними односторонними углами для параллельных прямых и и секущей Поэтому Аналогично это свойство можно доказать для любой другой пары соседних углов параллелограмма.

2. Параллелограмм является выпуклым четырехугольником.

3. В параллелограмме противолежащие стороны равны и противолежащие углы равны.

Доказательство:

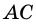
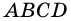
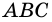
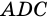
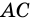
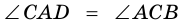
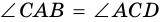
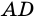
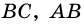
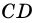
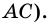
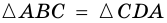
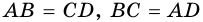
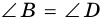
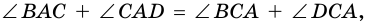
Диагональ разбивает параллелограмм на два треугольника и (рис. 17). -их общая сторона, и (как внутренние накрест лежащие углы для каждой из пар параллельных прямых и и и секущей Тогда (по стороне и двум прилежащим углам). Откуда, и (как соответственные элементы равных треугольников). Так как то

4. Периметр параллелограмма

5. Диагонали параллелограмма точкой пересечения делятся пополам.

Доказательство:

Пусть — точка пересечения диагоналей и параллелограмма (рис. 18). (как противолежащие стороны параллелограмма), (как внутренние накрест лежащие углы для параллельных прямых и и секущих и соответственно). Следовательно, (по стороне и двум прилежащим углам). Тогда (как соответственные стороны равных треугольников).

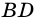
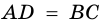
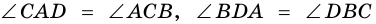
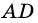
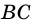
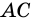
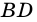
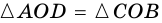
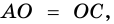
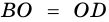
Пример:

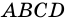
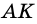
Дано: параллелограмм, — биссектриса угла (рис. 19). Найдите:

Решение:

1)

2) (как внутренние накрест лежащие углы для параллельных прямых и и секущей

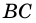
3) (по условию), тогда Тогда — равнобедренный (по признаку равнобедренного треугольника),

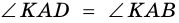
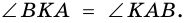
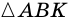
4)

Высотой параллелограмма называют перпендикуляр, проведенный из любой точки стороны параллелограмма к прямой, содержащей противолежащую сторону.

На рисунке 20 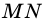— высота параллелограмма,

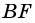
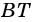
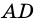
Из каждой вершины параллелограмма можно провести две высоты. Например, на рисунке 21 и — высоты параллелограмма, проведенные соответственно к сторонам и

Рассмотрим признаки параллелограмма.

Теорема (признаки параллелограмма). Если в четырехугольнике: 1) две стороны параллельны и равны, или 2) противолежащие стороны попарно равны, или 3) диагонали точкой пересечения делятся пополам, или 4) противолежащие углы попарно равны, — то четырехугольник является параллелограммом.

Доказательство:

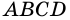
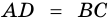
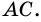
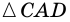
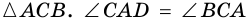
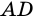
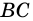
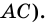
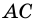
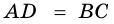
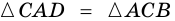
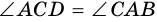
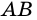
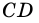
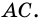
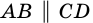
1) Пусть в четырехугольнике и (рис. 22). Проведем диагональ Рассмотрим и (как внутренние накрест лежащие при параллельных прямых и и секущей — общая сторона, (по условию). Следовательно, (по двум сторонам и углу между ними). Тогда (как соответственные). Но это накрест лежащие углы при пересечении прямых и секущей Поэтому (по признаку параллельности прямых). Следовательно, в четырехугольнике противолежащие стороны попарно параллельны. Поэтому -параллелограмм.

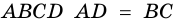
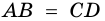
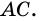
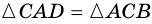
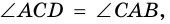
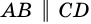
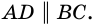
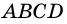
2) Пусть в четырехугольнике и (рис. 22). Проведем диагональ Тогда (по трем сторонам). Поэтому и следовательно, (по признаку параллельности прямых). Аналогично доказываем, что Следовательно, — параллелограмм.

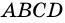
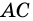
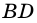
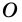
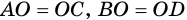
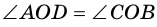
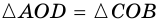
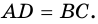
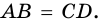
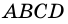
3) Пусть в четырехугольнике диагонали и пересекаются в точке и (рис. 23). (как вертикальные). Поэтому (по двум сторонам и углу между ними). Отсюда Аналогично доказываем, что Принимая во внимание п. 2) этой теоремы, приходим к выводу, что — параллелограмм.

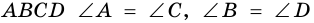
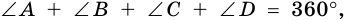
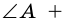
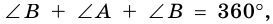
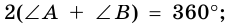
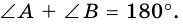
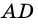
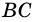
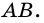
4) Пусть в параллелограмме (рис. 16). Так как то т. е. откуда Но и — внутренние накрест лежащие углы для прямых и и секущей Поэтому

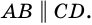
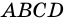
по признаку параллельности прямых). Аналогично доказываем, что Следовательно, — параллелограмм.

Пример:

В четырехугольнике 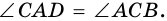Докажите, что — параллелограмм.

Доказательство:

Пусть — данный четырехугольник (рис. 22). Рассмотрим и — их общая сторона, (по условию). Тогда, (по двум сторонам и углу между ними). Следовательно, Но тогда в четырехугольнике противолежащие стороны попарно равны, поэтому он является параллелограммом.

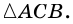
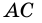
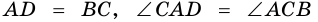
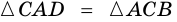
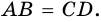
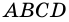
О некоторых видах четырехугольников (квадраты, прямоугольники, равнобокие и прямоугольные трапеции) знали еще древнеегипетские и вавилонские математики.

Термин «параллелограмм» греческого происхождения, считают, что он был введен Евклидом (около 300 г. до н. э.). Также известно, что еще раньше о параллелограмме и некоторых его свойствах уже знали ученики школы Пифагора («пифагорейцы»).

В «Началах» Евклида доказана следующая теорема: в параллелограмме противолежащие стороны равны и противолежащие углы равны, а диагональ делит его пополам, но не упоминается о том, что точка пересечения диагоналей параллелограмма делит каждую из них пополам.

Евклид также не упоминает ни о прямоугольнике, ни о ромбе.

Полная теория параллелограммов была разработана лишь в конце Средневековья, а в учебниках она появилась в XVII в. Все теоремы и свойства параллелограмма в этих учебниках основывались на аксиоме параллельности Евклида.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник