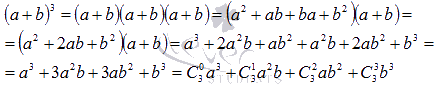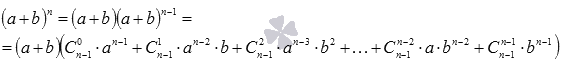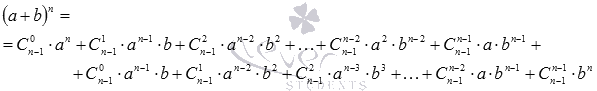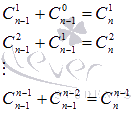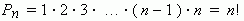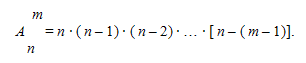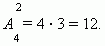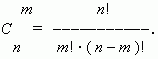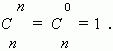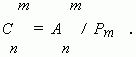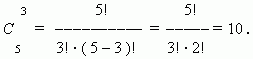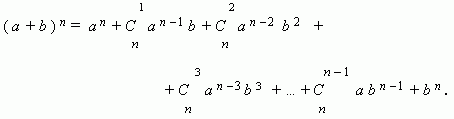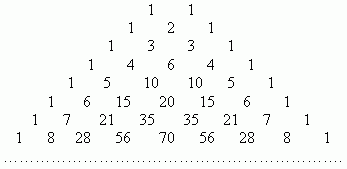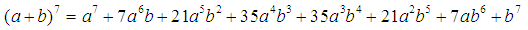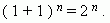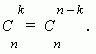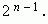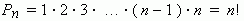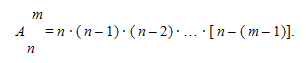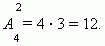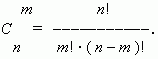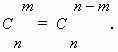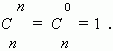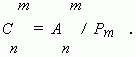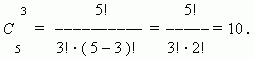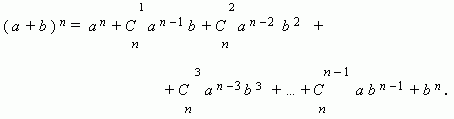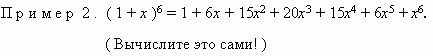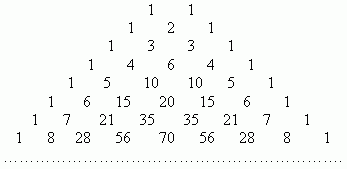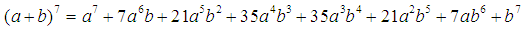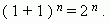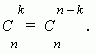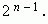Доказать что сумма биномиальных коэффициентов

Бином Ньютона.

Навигация по странице.

Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля.

Треугольник Паскаля.

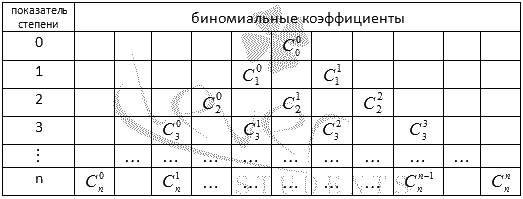
Биномиальные коэффициенты для различных n удобно представлять в виде таблицы, которая называется арифметический треугольник Паскаля. В общем виде треугольник Паскаля имеет следующий вид:

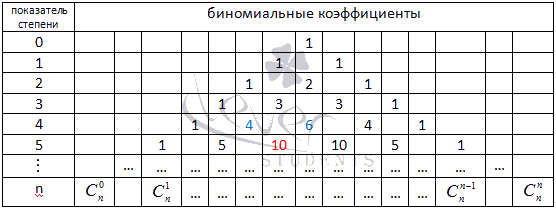
Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральных n :

Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.

Свойства биномиальных коэффициентов.

Первые два свойства являются свойствами числа сочетаний.

Доказательство формулы бинома Ньютона.

Приведем доказательство формулы бинома Ньютона, то есть докажем справедливость равенства .

Получили верное равенство.

Докажем, что верно равенство , основываясь на предположении второго пункта.

Поехали!

Раскрываем скобки

Группируем слагаемые

Так как и , то ; так как и , то ; более того, используя свойство сочетаний , получим

Подставив эти результаты в полученное выше равенство

придем к формуле бинома Ньютона .

Этим доказана формула бинома Ньютона.

Рассмотрим подробные решения примеров, в которых применяется формула бинома Ньютона.

Напишите разложение выражения (a+b) 5 по формуле бинома Ньютона.

Найдите коэффициент бинома Ньютона для шестого члена разложения выражения .

В заключении рассмотрим пример, в котором использование бинома Ньютона позволяет доказать делимость выражения на заданное число.

Доказать, что значение выражения , где n – натуральное число, делится на 16 без остатка.

Представим первое слагаемое выражение как и воспользуемся формулой бинома Ньютона:

Источник

Доказательство формулы бинома Ньютона.

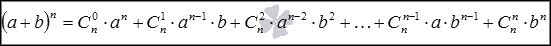
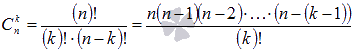
Формула бинома Ньютона для натуральных n имеет вид , где — биномиальные коэффициенты, представляющие из себя сочетания из n по k, k=0,1,2,…,n, а «!» – это знак факториала).

К примеру, известная формула сокращенного умножения «квадрат суммы» вида 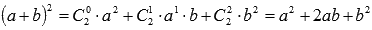есть частный случай бинома Ньютона при n=2.

Треугольник Паскаля.

Биномиальные коэффициенты для различных n удобно представлять в виде таблицы, которая называется арифметический треугольник Паскаля. В общем виде треугольник Паскаля имеет следующий вид:

Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральных n:

Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.

Свойства биномиальных коэффициентов.

Для коэффициентов бинома Ньютона справедливы следующие свойства:

· коэффициенты, равноудаленные от начала и конца разложения, равны между собой , p=0,1,2,…,n;

· ;

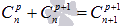
· сумма биномиальных коэффициентов равна числу 2, возведенному в степень, равную показателю степени бинома Ньютона: ;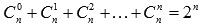

· сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах.

Первые два свойства являются свойствами числа сочетаний.

Доказательство формулы бинома Ньютона.

Приведем доказательство формулы бинома Ньютона, то есть докажем справедливость равенства .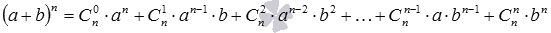

Воспользуемся для доказательства методом математической индукции.

1. Проверим справедливость разложения для какого-нибудь n, допустим, для n = 3.

Получили верное равенство.

2. Предположим, что равенство верно для n-1, то есть, что справедливо равенство .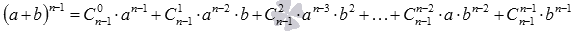

3. Докажем, что верно равенство 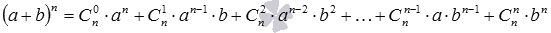, основываясь на предположении второго пункта.

Поехали!

Раскрываем скобки

Группируем слагаемые

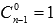
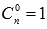
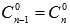
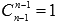
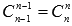
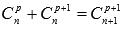
Так как и , то ; так как и , то ; более того, используя свойство сочетаний , получим

Подставив эти результаты в полученное выше равенство

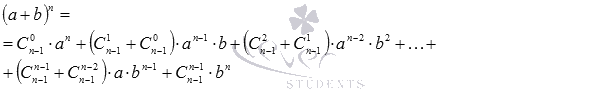
придем к формуле бинома Ньютона .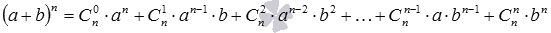

Этим доказана формула бинома Ньютона.

Общим термином «соединения» мы будем называть три вида комбинаций, составляемых из некоторого числа различных элементов, принадлежащих одному и тому же множеству (например, буквы алфавита, книги в библиотеке, машины на стоянке и т.д.).

Их общее количество обозначается: и равно произведению:

Вот эти размещения: ab, ba, ac, ca, ad, da, bc, cb, bd, db, cd, dc.

Их общее количество обозначается 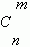и может быть вычислено по формуле:

Из этой формулы ясно, что

В соответствии с этим определением получим:

Общее число сочетаний можно вычислить, пользуясь и другим выражением:

Эти сочетания: abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde.

Бином Ньютона. Это формула, представляющая выражение ( a + b ) n при положительном целом n в виде многочлена:

Заметим, что сумма показателей степеней для a и b постоянна и равна n.

Числа 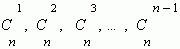называются биномиальными коэффициентами.

Их можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта схема называется треугольником Паскаля:

мы можем получить результат моментально, используя таблицу:

Свойства биномиальных коэффициентов.

Для доказательства достаточно положить a = b = 1. Тогда в правой части разложения бинома Ньютона мы будем иметь сумму биномиальных коэффициентов, а слева:

2. Коэффициенты членов, равноудалённых от концов разложения, равны.

Это свойство следует из соотношения:

3. Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна

Источник

11. Свойства биномиальных коэффициентов

Свойство 3 является следствием формулы бинома Ньютона:

. (9.1)

Поэтому сочетания еще иногда называют биномиальными коэффициентами.

Сумма биномиальных коэффициентов всех членов разложения равна 2n. Сумма биномиальных коэффициентов членов разложения, стоящих на нечетных местах, равна сумме биномиальных коэффициентов, стоящих на четных местах, и равно 2n–1.

Пример 9.1. Найти разложение степени бинома (2x–3)5.

Решение. Полагая a=2x, b=–3, получим

Пример 9.2. Пятый член разложения не зависит от x. Найти n.

Решение. Пятый член разложения T5 имеет следующий вид:

.

По условию T5 не зависит от x; это означает, что показатель степени при x равен нулю, т. е. (n–4)/3–4=0. Из последнего уравнения находим n=16.

Пример 9.3. Вычислить сумму

.

Решение. Согласно формуле бинома Ньютона, при любом x имеем равенство:

.

Полагая здесь x=1, получим

.

Итак, искомая сумма равна 35, т. е. 243.

9.1. Напишите разложение степени бинома

А) ; б) ; в) .

Ответ: а) ,

Б) ,

В) .

9.2. Найдите пятый член разложения .

Ответ: .

9.3. Найдите два средних члена разложения .

Ответ: и.

9.4. Найдите в биномиальном разложении член, не содержащий x.

Ответ: .

9.5. Найдите сумму .

Ответ: .

9.6. Сумма биномиальных коэффициентов разложения равна 64. Напишите член, не содержащий переменную x.

Ответ: n=6, .

Источник

Комбинаторика. Бином Ньютона

Перестановки. Факториал. Размещения. Сочетания.

Бином Ньютона. Биномиальные коэффициенты.

Треугольник Паскаля. Свойства биномиальных коэффициентов.

Общим термином «соединения» мы будем называть три вида комбинаций, составляемых из некоторого числа различных элементов, принадлежащих одному и тому же множеству (например, буквы алфавита, книги в библиотеке, машины на стоянке и т.д.).

Их общее количество обозначается: 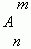и равно произведению:

Их общее количество обозначается 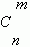и может быть вычислено по формуле:

Из этой формулы ясно, что

В соответствии с этим определением получим:

Общее число сочетаний можно вычислить, пользуясь и другим выражением:

Бином Ньютона. Это формула, представляющая выражение ( a + b ) n при положительном целом n в виде многочлена:

Числа 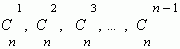называются биномиальными коэффициентами.

Их можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта схема называется треугольником Паскаля:

мы можем получить результат моментально, используя таблицу:

Свойства биномиальных коэффициентов.

Для доказательства достаточно положить a = b = 1. Тогда в правой части разложения бинома Ньютона мы будем иметь сумму биномиальных коэф фициентов, а слева:

2. Коэффициенты членов, равноудалённых от концов разложения, равны.

Это свойство следует из соотношения:

3. Сумма коэффициентов чётных членов разложения равна сумме коэффи циентов нечётных членов разложения; каждая из них равна

Источник

Сумма квадратов биномиальных коэффициентов

.

Как и при доказательстве основного свойства, используем равенство

(1+x) n = .

Умножим обе части этого равенства на (1+х) n :

(1+x) 2 n =

.

Так как слева и справа стоит один и тот же многочлен, то коэффициенты при х n слева и справа должны быть одинаковыми. Поэтому .

Другая, известная как треугольник Паскаля, интерпретация для биномиальных коэффициентов получается, если рассмотреть на бесконечной шашечной доске количество различных путей шашки от данной клетки до всех клеток доски.

Возьмем шахматную доску, ограниченную только с одной стороны, и поставим на поле A (черного цвета) нулевой горизонтали шашку. Двигаясь по правилам игры в шашки, она может попасть на любое поле черного цвета из области, ограниченной прямыми AB и AC. Напишем на каждом поле число способов, которыми можно попасть на данное поле. Получим

Эти числа обычно изображают в виде треугольника, при этом каждое число равно сумме двух элементов предыдущей строки, между которыми оно находится. Этот треугольник часто называют треугольником Паскаля, или арифметическим треугольником.

Арифметический треугольник можно записать и в таком виде:

Отметим еще следующие особенности арифметического треугольника: все элементы, расположенные выше главной диагонали, равны нулю, а нулевой столбец состоит из единиц. Числа, стоящие в n-й строке, являются коэффициентами в разложении бинома (1+x) n по степеням x. Поэтому их называют также биномиальными коэффициентами.

Решение. Пятая строка треугольника Паскаля имеет вид: 1 5 10 10 5 1. Поэтому

С помощью треугольника Паскаля можно доказать свойства биномиальных коэффициентов. (Смотри упражнения.)

Полиномиальной формулой называют формулу для вычисления значения выражений (x₁+x₂+…x_k) n для различного числа слагаемых и различных натуральных степеней n.

Теорема.

=

Доказательство.Формула доказывается аналогично формуле бинома Ньютона.

Раскроем скобки в правой части этого равенства и запишем все слагаемые в виде произведения n сомножителей x₁, x₂,…,x_k в том порядке, в котором они появляются. Получим всевозможные размещения с повторениями букв x₁, x₂,…,x_k, состоящие из n элементов. Используем коммутативность и приведем подобные члены. Подобными будут члены, содержащие одинаковое количество множителей x₁, x₂,…,x_k. Членов, в которые входит k₁ множителей х₁, k₂ множителей х₂ и так далее k_m множителей х_m, ровно Р(k₁,k₂,…k_m). Отсюда вытекает, что после приведения подобных членов выражение войдет с коэффициентом . Поэтому формула примет вид: .

Свойства чисел Р(k1k2…k3)

1. .

Доказательство.Если в полиномиальной формуле положить х₁=х₂=…=х_m=1, то получим требуемое равенство.

2. .

Доказательство.Умножим обе части равенства

на (х₁+х₂+…+х_m). Получим

.

Применим к левой части полиномиальную формулу, а в правой части раскроем скобки и рассмотрим коэффициент при . Слева он будет равен . В правой части член, содержащий , появится m раз: при умножении на х₁, при умножении на х₂ и так далее; коэффициент при будет равен . Слева и справа стоит один и тот же многочлен, следовательно, коэффициенты при слева и справа должны быть равны. Поэтому

.

Решение. Ясно, что коэффициенты при x 2 yz и xy 2 z равны. Поэтому достаточно найти коэффициенты для таких разбиений n=k₁+k₂+…k_m, что k_1³k_2³…_³k_m, а потом переставлять показатели всеми возможными способами. Для нашего примера имеем:

Задача. Сколькими способами можно замостить прямоугольную доску размером 2 × 7 костями домино, если все кости считать одинаковыми и учитывать только положение кости: горизонтальное или вертикальное?

Решение. Обозначим через Ф(k) количество способов замостить костями домино прямоугольную доску размером 2 × k. Угловая клетка может быть закрыта одним из двух способов: либо костью, которая лежит вертикально, тогда оставшуюся k–1 кость можно положить Ф(k–1) способами, либо костью, которая лежит горизонтально, тогда еще одну кость можем положить только горизонтально, а оставшиеся k–2 кости можно уложить Ф(k–2) способами. Используя правило суммы, приходим к соотношению Ф(к)=Ф(к–1)+Ф(к–2). Учитывая, что Ф(0)=Ф(1)=1, можем для любого значения k найти ответ: Ф(2)=2, Ф(3)=3, Ф(4)=5, Ф(5)=8, Ф(6)=13, Ф(7)=21. Имеем 21 способ замостить костями домино прямоугольную доску размером 2 × 7.

При решении многих комбинаторных (и не только) задач часто встречается способ, когда задачу с заданными значениями параметров сводят к аналогичной задаче, но уже с меньшими значениями параметров. Таким образом, можно довести задачу до простой. Данный метод решения задач носит название метода рекуррентных соотношений. (От латинского слова recurrere – «возвращаться»).

Пример.Используя метод рекуррентных соотношений, можно по-новому вывести формулу для вычисления числа перестановок из k предметов.

Обозначим за Р(k) количество перестановок из элементов k типов. В перестановке на первом месте может быть любой из k предметов, а оставшиеся k–1 предметов можно в каждом из этих случаев переставить Р(k–1) способами. По правилу произведения получаем формулу Р(k)=k∙Р(k-1). Далее замечаем, что Р(1)=1, и получаем, что Р(k)=k!

Числа Фибоначчи

Формула, которую мы получили при решении задачи о домино, впервые была опубликована в книге «Liber Abaci», появившейся в 1202 году, где итальянский математик Фибоначчи среди многих других задач привел следующую:

Пара кроликов приносит раз в месяц приплод из двух крольчат (самки и самца), причем новорожденные крольчата через два месяца после рождения уже приносят приплод. Сколько кроликов появится через год, если в начале года была одна пара кроликов?

Из условия задачи следует, что через месяц будет две пары кроликов. Через два месяца приплод даст только первая пара кроликов, и получится 3 пары. А еще через месяц приплод дадут и исходная пара кроликов, и пара кроликов, появившаяся два месяца тому назад. Поэтому всего будет 5 пар кроликов.

Обозначим через F(n) количество пар кроликов по истечении n месяцев с начала года. Мы видим, что через n+1 месяцев будут эти F(n) пар и еще столько новорожденных пар кроликов, сколько было в конце месяца n–1, то есть еще F(n–1) пар кроликов. Иными словами, имеет место рекуррентное соотношение

Так как, по условию, F(0)=1 и F(1)=2, то последовательно находим

Полученные числа называют числами Фибоначчи.

Чтобы найти F(12), нам придется последовательно вычислить F(3), F(4), … F(11), что достаточно долго. А если нам необходимо было бы вычислить F(100), то это займет еще больше времени. Попробуем выразить закономерность последовательности Фибоначчи с помощью расчетной формулы (вместо неявного рекуррентного соотношения). Для этого присвоим двоичный номер каждой паре кроликов. Единицам соответствуют месяцы появления на свет одной из пар «предков» данной пары (включая и исходную), а нулями – все остальные месяцы. Например, последовательность 010010100010 устанавливает такую «генеалогию» – сама пара появилась в конце 11-го месяца, ее родители – в конце 7-го месяца, «дед» – в конце 5-го месяца, «прадед» – в конце 2-го месяца. Исходная пара кроликов зашифровывается при этом последовательностью 000000000000. В последовательности не могут идти подряд две единицы, так как кролики приносят приплод только на второй месяц после рождения.

Тем самым устанавливается связь между числами Фибоначчи и следующей комбинаторной задачей: найти число n-последовательностей, состоящих из нулей и единиц, в которых никакие две единицы не идут подряд. Число таких последовательностей, в которые входит ровно k единиц и n–k нулей, равно . Так как при этом должно выполняться неравенство k

Источник