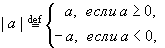Доказать что sup x y supx supy
Арифметические свойства верхних и нижних граней.
Арифметические свойства верхних и нижних граней.
Арифметические свойства верхних и нижних граней. Семьдесят пять X, Y, U Во-первых, мы определяем такую операцию. Арифметическая сумма набора чисел X1 + … + Хп… Xn, x = x + … + xn, x∈X,… это множество всех чисел x, которые могут быть выражены в виде xn∈Xn. Арифметическая разность X-Y в числовом множестве X и Y представляет собой множество всех числовых значений r и может быть выражена в виде r = x-y, x∈X, y∈. Конечно, арифметическая сумма х + … + Понятие XN и разность X-Y, теоретико-множественная сумма (sum) X Y … Различие одного и того же множества с Y Xn следует отличать от понятия X \ Y. Произведение числа 1 на 1X и набора чисел X представляет собой набор всех чисел в виде 1x, x∈X. Произведение 2-х множеств чисел X и Y X Y есть множество чисел r, которое может быть выражено в виде r = xy, x€.
Рассмотрим 4 свойства верхней и нижней сторон множества, которые связаны с арифметическими операциями над набором чисел. Людмила Фирмаль
Теорема о наличии верхней и нижней поверхностей указывает на 2 важных свойства вещественных чисел, Принцип 1 так называемого Архимеда и принцип вложенного отрезка. Людмила Фирмаль
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Числовые множества. 2.1 Свойства действительных чисел.
2.1 Свойства действительных чисел.
Для любых двух чисел а и b определено единственным способом число, называемое их суммой и обозначаемое a+b. Сумма обладает свойствами:
1. Для любых двух a и b: a+b=b+a. Это свойство называется переместительным (коммутативным) законом сложения.
2. Для любых a,b,c: a+(b+c)=(a+b)+c. Это свойство называется сочетательным (ассоциативным) законом сложения.
3. Существует число 0, называемое нулем, такое, что для любого числа а: а+0=а.
4. Для любого а существует такое число, обозначаемое –а и называемое противоположным данному, такое, что а+(-а)=0.
Далее, вместо а+(-b) будем писать а-b.
Для любых двух чисел а и b определено единственным способом число, называемое их произведением и обозначаемое а·b. Произведение обладает свойствами:
5. Для любых чисел а и b: а·b=b·а. Это свойство называется переместительным (коммутативным) законом умножения.
6. Для любых чисел a,b,c: a·(b·c)= (a·b)·c. Это свойство называется сочетательным (ассоциативным) законом умножения.
7. Существует число 1, называемое единицей, такое, что для любого числа а: а·1=а.
8. Для любого числа а≠0 существует число, называемое обратным для а и обозначаемое 1/а, такое, что а·(1/а)=1.
Cвязь операций сложения и умножения.
9. Для любых чисел а, b, c: (a+b)·c = a·c + b·c. Это свойство называется распределительным (дистрибутивным) законом умножения относительно сложения.
Для любых двух чисел a и b справедливо одно из соотношений: а b (а больше b) так, что выполняются свойства:
10. Если а>b, то для любого с: а+с>b+с.
11. Если а>b, то для любого с>0: а·c>b·c.
12. Каковы бы ни были непустые множества А 
R, В R, у которых для любых элементов аєА, bєB выполняется неравенство а≤b, всегда существует такое число z 
, что для всех хєА, уєВ: х≤z ≤у.
2.2 Числовые промежутки
Отрезок, интервал, полуинтервал записываются соответственно как
2.3 Точные грани числовых множеств
Множество X действительных чисел (X Ì R) называется ограниченным сверху, если существует число с Î R такое, что все элементы множества X не превосходят с, т.е.
$ с Î R: «x 
X x ≤ с.
Множество X Ì R называется ограниченным снизу, если существует число d Î R такое, что все элементы множества X не меньше d, т.е.
$ d Î R : «x X x ³ d.
Множество X Ì R называется ограниченным, если оно ограничено как сверху, так и снизу, т.е.
Последнее условие равносильно условию
$ g Î R : «x X | x | ≤ g.
Если множество Х ограничено сверху, то наименьшее из чисел, ограничивающее его сверху, называют его супремумом (supremum).
Число a является супремумом множества Х, если выполняются следующие условия:
1) » x X x ≤ a;
Cупремум множества Х обозначается sup X.
Если множество Х ограниченно снизу, то наибольшее из чисел, ограничивающее его снизу, называют его инфимумом (infimum).
Число b является инфимумом множества Х, если выполняются следующие условия:
1) » x X x ³ b;
5) Неравенство |x| ³ a (a >0) означает, что либо х ³ a, либо х ≤-a;
9) | 
| = 
(y ¹ 0).
ПРИМЕРЫ С РЕШЕНИЯМИ
Решение. При любом натуральном n выполняются неравенства 0 0 существует 1/n такое, что выполняется неравенство
Докажем теперь, что число 0 является инфимумом множества X. Для этого надо проверить, что для любого e>0 существует 
такое, что выполняется неравенство
. И взяв какое-нибудь натуральное число n > , получим требуемое n, а это, согласно определению инфимума, и означает, что inf X = 0.
Решение. 1) При х ³0 х = х + 2, откуда вытекает, что 0 = 2 и т.е. вытекает, что наше уравнение не имеет решений.
Решение. Так как |x |> x только при х 0, что аn>b.
Задача 7. Пусть X и Y — два непустых множества действительных чисел. Доказать, что если Y Ì X, то: a) sup Y ≤ sup X; б) inf Y ³ inf X.
Задача 8. Пусть X и Y — два непустых множества чисел, а X+Y – множество всевозможных чисел вида x+y; где xÎX, yÎY. Показать, что sup (X+Y) = sup X + sup Y; inf (X+Y) = inf X + inf Y.
Задача 9. Пусть X и Y — два непустых числовых множества неотрицательных действительных чисел, а XY – множество всевозможных чисел вида xy; где xÎX, yÎY. Показать, что sup (XY) = (sup X)×(sup Y); inf (X·Y) = (inf X)×(inf Y).
Задача 11. Пусть X и Y — два непустых множества неотрицательных действительных чисел, а X-Y – множество всевозможных чисел вида x-y; где xÎX, yÎY. Показать, что sup (X-Y) = (supX) – (infY).
Задача 12. Решить уравнения и неравенства:
г) | 
| = .
Задача 14. Решить уравнения и неравенства:
Задача 15. Решить уравнения:
а) |sin x|- sin x =2; б) x 2 – 2|x| + 3= 0.
Задача 16. Решить уравнения и неравенства:
Задача17. Решить уравнения и неравенства:
Задача 18. Решить неравенства:
Дата добавления: 2015-01-12 ; просмотров: 14 | Нарушение авторских прав
Существование верхней (нижней) грани.
Докажем еще одну теорему, которая опирается на свойство непрерывности действительных чисел.
Терема о существовании верхней (нижней) грани.Сначала введем несколько определений.
Определение. Числовое множество X называется ограниченным, если оно ограничено сверху и снизу.
В символической записи эти определения будут выглядеть следующим образом:
ограничено снизу, если ∃m ∀x ∈ X : x ≥ m и
Пустое множество будем считать ограниченным по определению.
Определение. Для любого числа a 
R неотрицательное число
называется его абсолютной величиной или модулем. Для абсолютных величин чисел справедливо неравенство |a+b|
Теорема 4.3.1. Числовое множество X ограничено тогда и только тогда, когда существует число C такое, что для всех элементов x из этого множества выполняется неравенство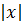 
≤ C.
Очевидно, что равенство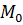 
= sup X равносильно двум условиям:
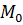
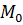
1) ∀x ∈ X выполняется неравенство x ≤ , т.е. — верхняя граница множества X ;
1) ∀x ∈ X выполняется неравенство x ≥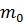 
;
2) ∀ε > 0 ∃xε ∈ X так, что выполняется неравенство xε 
Чтобы доказать противоположное неравенство, возьмем число y
Пусть
C cуммой я вроде справился, а тут совсем непонятно
задан 24 Сен 12:55
sanyapp
25 ● 1 ● 5
77% принятых
@sanyapp: под
Для случая неотрицательных чисел утверждение очевидно, и доказывается точно так же, как и для суммы.
@caterpillar не понял про нестрогое неравенство @falcao формулировка такая дана в демидовиче, то что xy (24 Сен 16:24) sanyapp
@sanyapp, приведите свои рассуждения для случая суммы. Чтобы стало понятнее, в каком месте Вы не видите, что они повторяются и для произведения. И я не писал про нестрогое неравенство. Я писал про строгое.
@sanyapp: а можно ссылку на страницы задачника?
Доказательство в другую сторону (на содержательном уровне) такое: полагаем a=sup X, b=sup Y. Берём eps > 0. Находим в X точку x > a-eps. В Y находим точку y > b-eps. Тогда при достаточно малом eps будет xy > (a-eps)(b-eps). Устремляем eps к нулю (справа). Это даст sup(XY)>=ab.
@caterpillar: я хотел своими глазами такие обозначения увидеть. Жаль, что в переизданиях классического задачника оставляют явную «архаику».
@sanyapp: если пределы пока не изучались, то достаточно рассмотреть разницу между числами и оценить её сверху: ab-(a-eps)(b-eps) (24 Сен 23:37) falcao
@falcao cтраница 11 http://pm-pu.ru/stuff/analiz/books/demidovich_sbornik.pdf на 8мой странице есть определение sup и inf, с 1 пунктом у меня получилось, а вот второй пункт пока нет. Мне надо как-то показать, что для любого еps>0 сущ. x’y’ принадл.
Ну, считайте, что c=ab-eps. При рассуждении от противного это будет мажорантой (да, верхней границей) для XY. Но это вполне бессмысленное занятие так расписывать.
@sanyapp: выше всё было подробно расписано с участием eps на вполне формальном уровне.
Доказать, что множества чисел бесконечны
доброго времени суток. Объясните мне пожалуйста, с чего вообще начинается доказательство кагого.
Доказать, что противоположные стороны четырёхугольника равны между собой.
1. диагонали четырехугольника пересекаются в точке О, причем одна из диагоналей этой точкой.
У вас путаное объяснение и вы не учитываете возможность бесконечности, но принцип правильный.
Действуйте ясно. Вам требуется доказать, что нижняя грань некоторого множества будет равна такому-то числу. По определению для этого нужно убедиться, что 1) данное число является нижней границей; 2) никакое число, большее данного, не является нижней границей.
Даны два множества. Найти произведение элементов одновременно принадлежащим обоим множествам.
Даны два множества. Найти произведение элементов одновременно принадлежащим обоим множествам.
Доказать что множества эквивалентны
Докажите, что множества А= <точки на параболе>и В= <точки эллипса>эквивалентны на пополненной.
Доказать, что мощность множества счетна
Здравствуйте. Как доказать, что мощность множества рациональных чисел счетна?