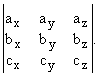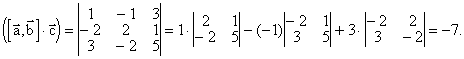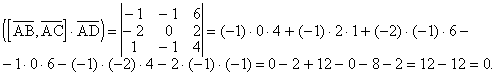Доказать что три вектора компланарны

Компланарность векторов. Условия компланарности векторов.

Всегда возможно найти плоскости параллельную двум произвольным векторам, по-этому любые два вектора всегда компланарные.

Условия компланарности векторов

Примеры задач на компланарность векторов

Решение: найдем смешанное произведение векторов

Ответ: вектора не компланарны так, как их смешанное произведение не равно нулю.

Решение: найдем смешанное произведение векторов

Ответ: вектора компланарны так, как их смешанное произведение равно нулю.

Решение: найдем количество линейно независимых векторов, для этого запишем значения векторов в матрицу, и выполним над ней элементарные преобразования

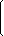	1	1	1
	1	2	0
	0	-1	1
	3	3	3

из 2-рой строки вычтем 1-вую; из 4-той строки вычтем 1-вую умноженную на 3

к 3-тей строке добавим 2-рую

Так как осталось две ненулевые строки, то среди приведенных векторов лишь два линейно независимых вектора.

Ответ: вектора компланарны так, как среди приведенных векторов лишь два линейно независимых вектора.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №18. Компланарные векторы. Векторный метод решения задач

Перечень вопросов, рассматриваемых в теме:

— какие векторы называются компланарными и их изображение на чертежах

-определение компланарных векторов.

— признак компланарности трех векторов и правило параллелепипеда, сложение трех некомпланарных векторов.

— основы векторного метода решения задач.

Ершова А.П., Голобородько В.В., Крижановский А.Ф. Тетрадь-конспект по геометрии для 10 класса. 2016. С.88-93.

Теоретический материал для самостоятельного изучения:

Давайте вспомним основные определения по теме «Векторы». В этом поможет следующее задание: установите соответствие между понятием и его определением.

Противоположно направлены и их длины равны.

Сонаправлены и их длины равны.

Лежат на одной или параллельных прямых

Определение2.Векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.

Рассмотрим некоторые случаи:

1 случай. Любые два вектора всегда будут компланарными, ведь через них
можно провести прямые, а через две прямые всегда можно провести
единственную плоскость.

2 случай. Три вектора будут компланарными если среди них есть пара коллинеарных
векторов. Тогда через один из коллинеарных векторов и вектор не коллинеарный ему
можно провести плоскость. А для второго из коллинеарных векторов легко
изобразить равный в этой плоскости.

3 случай. Если хотя бы один из трёх векторов является нулевым, то эти три вектора компланарны

Из планиметрии: Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.

Теорема. Любой вектор можно разложить по трём данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.

Часть 2. Векторный метод решения задач

Векторный метод решения задач – один из наиболее общих методов решения геометрических задач. Векторное решение стереометрических задач значительно проще их решения средствами элементарной геометрии.

Рассмотрим следующую задачу: Доказать, что прямая, проведенная через середины оснований трапеции, проходит через точку пересечения продолжений боковых сторон.

Докажем, что точка О лежит на прямой МN.

Условие задачи переводится на «векторный» язык. После такого перевода осуществляются алгебраические вычисления с векторами, а затем полученное снова «переводится» на «геометрический» язык.

Решением задач векторным методом занимались ученые: Уильман Гамильтон Иога́нн Берну́лли, Пьер Ферма, Рене Декарт, Леонард Эйлер.

Примеры и разбор решения заданий тренировочного модуля:

Задача. В параллелепипеде АВСDА₁В₁С₁D₁ М —точка пересечения диагоналей грани A₁B₁C₁D₁, точка K — середина ребра ВВ₁. Докажите, что прямые А₁В₁, KМ и ВС₁ параллельны некоторой плоскости.

Решение. Введем векторы: . Векторы некомпланарны.

Разложим векторы и по векторам. Получим:

+= .

Тогда векторы = + компланарны. Следовательно, они параллельны некоторой плоскости, тогда этой плоскости параллельны и прямые А₁В₁, KМ и ВС₁.

Источник

Какие векторы называют компланарными

Компланарные векторы – это векторы, которые лежат в одной плоскости, или параллельны какой-либо плоскости.

Рассмотрим три вектора в трехмерном пространстве. Любые два из них будут компланарными всегда. Поэтому, компланарность проверяют минимум для трех векторов.

Почему любые два вектора всегда компланарны

Поясним факт, что любые два вектора будут компланарными.

Для начала вспомним, какие векторы называют равными. Равны векторы, у которых совпадают три характеристики: длина, направление, соответственные координаты.

При параллельном переносе вектор не поворачивается. Этот новый вектор \( \vec> \) будет иметь те же длину, направление и координаты, что и начальный вектор до сдвига. Другими словами, с помощью параллельного переноса можно получить вектор, равный данному вектору.
\[ \vec = \vec> \]

Если два вектора равны, то вместо одного из них мы сможем использовать второй, когда это будет удобным для нас.

Проделаем теперь те же операции с каким-либо другим вектором \( \vec \). В результате получим вектор \( \vec> \), равный вектору \( \vec \).

Любые два вектора можно параллельным переносом сдвинуть так, чтобы совместить их начальные, или конечные точки. Значит, через эти векторы можно провести пересекающиеся прямые. А такие прямые будут лежать в одной плоскости.

Таким образом, любые два вектора всегда компланарны.

Например, любые два орта Декартовой прямоугольной системы координат компланарны, а тройка ортов – некомпланарные векторы. Подробнее об ортах тут (откроется в новой вкладке).

Условие компланарности

Найдем смешанное произведение трех векторов.

Если такое произведение будет равно нулю, то три вектора компланарные.

Условие компланарности векторов:
\[\large \boxed < \left( \vec, \vec , \vec \right) = 0 >\]

Как вычислить смешанное произведение

Смешанное произведение можно обозначить еще одним способом:

Результат смешанного произведения – это число. Если число равно нулю, то векторы компланарны.

Как применять смешанное произведение

Если три вектора не компланарны, то на них, как на сторонах, можно построить параллелепипед, или пирамиду.

С помощью смешанного произведения можно рассчитывать объемы параллелепипедов или треугольных пирамид, построенных на трех некомпланарных векторах.

Примечание:
Определитель может быть равен отрицательному числу. А объем может быть либо нулевым, либо положительным. Поэтому, если при вычислении объема определитель будет равен отрицательному числу, знак минус не учитываем.

Рисунок 2 поясняет, как с помощью векторов на ребрах параллелепипеда можно рассчитать его объем

Рисунок 3 поясняет, как с помощью векторов на ребрах пирамиды можно рассчитать ее объем

Смешанное произведение векторов в физике — работа вращающей силы

Пусть цилиндрическое тело вращается под действием силы. Ось вращения проходит через ось симметрии тела.

Работа вращающей силы – это смешанное произведение векторов \( \vec <\omega>\), \(\vec < r>\) и \(\vec < F>\)

\[ \large \boxed < dA = \left( \vec\left[ \vec <\omega>, \vec \right] \right)\cdot dt >\]

Пояснения:

Линейная скорость – это векторное произведение радиуса окружности на угловую скорость:

Расстояние, \( \vec\) которое проходит точка при повороте на небольшой угол — – это произведение вектора линейной скорости на скалярную величину – время:
\[ \vec = v \cdot dt \]

Небольшая работа dA – это скалярное произведение вектора силы на вектор перемещения
\[ dA = \left( \vec \cdot \vec \right)\]

Источник

Глава 18. Смешанное произведение векторов. Условие компланарности трех векторов

Смешанным произведением трех векторов A, B и C Называется произведение, составленное следующим образом: ([A,B]×C), т. е. два вектора A и B умножаются векторно, а затем полученный вектор [A,B] скалярно умножается на третий вектор C. Смешанное произведение – это Число.

Если известны координаты перемножаемых векторов A = , B = , C = , то их смешанное произведение можно вычислить по формуле:

([A,B]×C) =

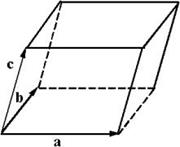
С геометрической точки зрения смешанное произведение векторов A, B И C с точностью до знака равно объему параллелепипеда, построенного на этих векторах, как на ребрах (рис. 2.4.1).

Вычислить объем треугольной пирамиды, построенной на векторах A = <1, –1, 3>, B = <–2, 2, 1>и C = <3, –2, 5>.

Вычислим смешанное произведение векторов:

(ед.3).

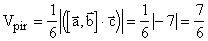
Выяснить, лежат ли точки A(1,2,–1), B(0,1,5), C(–1,2,1) и D(2,1,3) в одной плоскости.

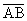
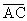
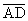
Очевидно, точки A, B и C лежат в одной плоскости, если векторы , и компланарны.

Условием Компланарности трех векторов является Равенство нулю их смешанного произведения.

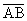
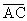
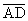
Найдем компоненты векторов: = <0–1, 1–2, 5–(–1)>= <–1, –1, 6>; = <–1–1, 2–2, 1–(–1)>= <–2, 0, 2>;

= <2–1, 1–2, 3–(–1)>= <1, –, 4>. Вычислим смешанное произведение:

Так как смешанное произведение равно нулю, то вектора компланарны, а значит точки A, B, C и D лежат в одной плоскости.

Источник

Доказать что три вектора компланарны

Определение. Три вектора, параллельные одной плоскости или лежащие в одной плоскости, называются компланарными.

Пусть три вектора а, b, с компланарны. Не ограничивая общности, можно считать, что эти векторы лежат в одной плоскости.

В этом случае вектор будет перпендикулярен этой плоскости и, следовательно, перпендикулярен вектору с, поэтому скалярное произведение

Следовательно, смешанное произведение компланарных векторов равно нулю.

Обратно, если смешанное произведение , то векторы а, b, с компланарны.

Действительно, если бы эти векторы были бы не компланарны, то на них можно было бы построить параллелепипед с объемом . Но так как , то отсюда следовало бы, вопреки предположению, что .

Итак, для того чтобы три вектора а, b, с были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю, т. е.

Рассмотрим теперь примеры на применение смешанного произведения векторов.

Пример 1. Показать, что векторы компланарны.

Решение. Составляем смешанное произведение этих векторов:

Так как смешанное произведение оказалось равным нулю, то, следовательно, векторы компланарны.

Пример 2. Вычислить объем пирамиды с вершинами в точках .

Решение. Рассмотрим векторы

Из элементарной геометрии известно, что объем пирамиды, построенной на ребрах ОЛ, ОВ и ОС, равен объема параллелепипеда, построенного на тех же ребрах.

(при вычислении определителя мы воспользовались разложением по элементам третьего столбца).

Источник