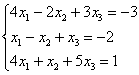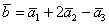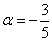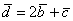Доказать что три вектора образуют базис
Доказать, что 3 вектора образуют базис трёхмерного пространства и найти координаты 4-го вектора в данном базисе
Даны векторы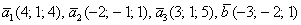 
. Показать, что векторы 
образуют базис трехмерного пространства и найти координаты вектора 
в этом базисе.
Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора вполне могут образовывать новый базис. И первый этап полностью совпадает с решением Примера 6, необходимо проверить, действительно ли векторы линейно независимы:
Вычислим определитель, составленный из координат векторов :
, значит, векторы линейно независимы и образуют базис трехмерного пространства.
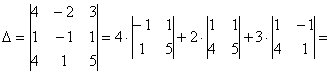
! Важно: координаты векторов обязательно записываем в столбцыопределителя, а не в строки. Иначе будет путаница в дальнейшем алгоритме решения.
Теперь вспомним теоретическую часть: если векторы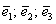 
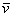
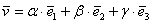
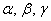
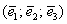
образуют базис, то любой вектор 
можно единственным способом разложить по данному базису: 
, где 
– координаты вектора в базисе 
.
Поскольку наши векторы образуют базис трёхмерного пространства (это уже доказано), то вектор 
можно единственным образом разложить по данному базису:
, где 
– координаты вектора в базисе 
.
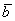
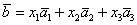
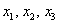
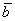
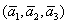
По условию и требуется найти координаты .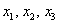
Для удобства объяснения поменяю части местами: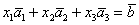 
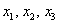
. В целях нахождения следует расписать данное равенство покоординатно: 
По какому принципу расставлены коэффициенты? Все коэффициенты левой части в точности перенесены из определителя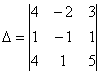 
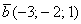
, в правую часть записаны координаты вектора 
.
Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают поформулам Крамера, часто даже в условии задачи есть такое требование.
Главный определитель системы уже найден:
, значит, система имеет единственное решение.
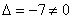
Дальнейшее – дело техники: 
Таким образом:
– разложение вектора по базису 
.
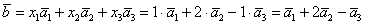
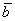
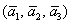
Ответ: 
Как я уже отмечал, задача носит алгебраический характер. Векторы, которые были рассмотрены – это не обязательно те векторы, которые можно нарисовать в пространстве, а, в первую очередь, абстрактные векторы курса линейной алгебры. Для случая двумерных векторов можно сформулировать и решить аналогичную задачу, решение будет намного проще. Однако на практике мне такое задание ни разу не встречалось, именно поэтому я его пропустил в предыдущем разделе.
Такая же задача с трёхмерными векторами для самостоятельного решения:
Даны векторы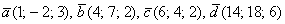 
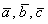
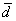
. Показать, что векторы 
образуют базис и найти координаты вектора 
в этом базисе. Систему линейных уравнений решить методом Крамера.
Полное решение и примерный образец чистового оформления в конце урока.
Аналогично можно рассмотреть четырёхмерное, пятимерное и т.д. векторные пространства, где у векторов соответственно 4, 5 и более координат. Для данных векторных пространств тоже существует понятие линейной зависимости, линейной независимости векторов, существует базис, в том числе, ортонормированный, разложение вектора по базису. Да, такие пространства невозможно нарисовать геометрически, но в них работают все правила, свойства и теоремы двух и трех мерных случаев – чистая алгебра. Собственно, о философских вопросах меня уже пробивало поговорить в статье Частные производные функции трёх переменных, которая появилась раньше данного урока.
Любите векторы, и векторы полюбят вас!
Пример 2: Решение: составим пропорцию из соответствующих координат векторов:
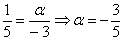
Ответ: при 
Пример 4: Доказательство: Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
1) Проверим параллельность противоположных сторон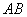 
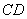
и 
.
Найдём векторы:
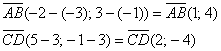
Вычислим определитель, составленный из координат векторов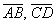 
:
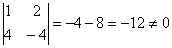
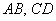
, значит, данные векторы не коллинеарны, и стороны 
не параллельны.
2) Проверим параллельность противоположных сторон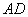 
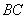
и 
.
Найдём векторы:
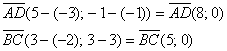
Вычислим определитель, составленный из координат векторов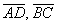 
:
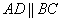
, значит, данные векторы коллинеарны, и 
.
Вывод: Две стороны четырёхугольника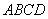 
параллельны, а две другие стороны не параллельны, значит, он является трапецией по определению. Что и требовалось доказать.
Пример 5: Решение:
б) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:
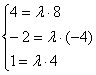
Система не имеет решения, значит, векторы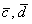 
не коллинеарны.
Более простое оформление:
– вторая и третья координаты не пропорциональны, значит, векторы не коллинеарны.
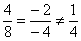
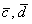
Ответ: векторы 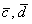не коллинеарны.
в) Исследуем на коллинеарность векторы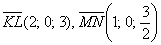 
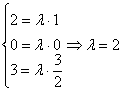
. Составим систему:
Соответствующие координаты векторов пропорциональны, значит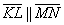 
Вот здесь как раз не проходит «пижонский» метод оформления.
Ответ:
Пример 6: Решение: б) Вычислим определитель, составленный из координат векторов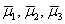 
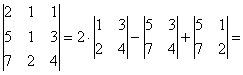
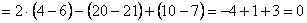
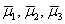
(определитель раскрыт по первой строке):
, значит, векторы линейно зависимы и не образуют базиса трёхмерного пространства.
Ответ: данные векторы не образуют базиса
Пример 9:Решение:Вычислим определитель, составленный из координат векторов :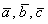
Таким образом, векторы 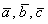линейно независимы и образуют базис.
Представим вектор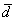 
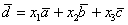
в виде линейной комбинации базисных векторов:
Покоординатно:
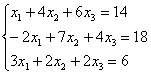
Систему решим по формулам Крамера:
, значит, система имеет единственное решение.
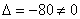
Ответ: Векторы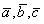 
образуют базис, 
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Векторное произведение векторов.
Смешанное произведение векторов
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов. Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов, требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение, даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урокаВекторы для чайников, чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы, а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
35. Базис векторов пространства
Рассмотрим множество V3 всех векторов пространства.
Теорема 5. Любая упорядоченная система трех некомпланарных векторов A, B, С € V3 Образуют базис векторного пространства V3.
Доказательство. Пусть A, B, С Некомпланарные векторы. По следствию 1 теоремы 8 они образует линейно независимую систему. Пусть D € V3. Отложим векторы A, B, С и D от точки O: A =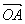 
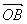
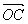
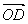
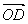
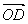
, B = 
, С = 
, D = 
(см. рис. 18). Проведем через точку D прямую L, параллельную прямой OD. Так как векторы A, B, С некомпланарны, то прямая L пересекает плоскость OAB в точке E. Тогда =
+
. Так как векторы лежит в плоскости OAB, а вектора образуют базис векторов этой плоскости, то по теореме 7 = a a + b b, где a, b € R. Так как вектор коллинеарен вектору C, То по теореме 8 § 1 он линейно выражается через вектор С: = g с. Поэтому D = = a a + b b + g с и по определению 1 вектора A, B, С образует базис пространства V3.
По теореме 5 базис векторов на пространстве образуют любые три некомпланарные вектора, поэтому любой вектор в пространстве имеет три координаты. Тогда справедливо следующее утверждение.
Следствие 1. Вектора A = (a1, b1, g1), B = (a2, b2, g2), С = (a3, b3, g3) Образуют базис векторов пространства тогда и только тогда, когда
= 0.
Теорема 6. Любые четыре вектора A, B, С, D В пространстве линейно зависимы.
Доказательство. Если векторы A, B, С Компланарны, то по теоремы 5 они линейно зависимы. Тогда по свойству линейной зависимости по свойству 4 § 3 вектора A, B, С, D линейно зависимы. Если вектора A, B, С некомпланарны, то по теореме 5 они образуют базис векторов пространства. Тогда вектор D линейная комбинация векторов A, B, С и по свойству линейной зависимости векторы A, B, С, D линейно зависимы.
Решение. Так как определитель
,
Для того, чтобы найти координаты вектора D в базисе A, B, С составим векторное уравнение
И запишем его в координатной форме:
Доказать что векторы образуют базис
Доказать, что векторы образуют базис
Помогите,пожалуйста, решить. Доказать,что векторы a, b, c, образуют базис, и найти координаты.
Доказать, что векторы a, b, c образуют базис, и
Доказать, что векторы a, b, c образуют базис, и разложить вектор d по этому базису.
Доказать, что данные векторы образуют базис, и найти координаты вектора D
Даны векторы. a(10:3:1) b(1:4:2) c(3:9:2) d(19:30:7) показать что они образуют базис и найти.
Доказать что векторы a, b, c образуют базис и найти координаты вектора b в этом базисе
Доказать что векторы a, b, c образуют базис и найти координаты вектора d в этом базисе Помагите.
Решение
Чтобы доказать тот факт, что три вектора образуют базис, достаточно доказать их линейную независимость. В свою очередь для этого достаточно доказать, что определитель, приведенный ниже, не равен нулю.
Вычитая из первого столбца сумму второго и третьего столбца, получим:
раскладывая последний определитель по элементам 1-го столбца, получаем, что наш определитель равен 10*(4*3+1)=130
Определитель не равен нулю, значит вектора линейно-независимы. А поскольку координат три и векторов три, то они образуют базис.
Показать, что векторы образуют базис.
Помогите плиз, в геометрии полный 0 =( Все остальные задания сделал, а это вообще не могу.
Показать, что векторы образуют базис и найти в нем координаты данного вектора
Показать, что векторы a, b,c образуют базис и найти в нем координаты вектора m. а=(2;-2;1).
Даны векторы а(2;7;3) b(3;1;8) с(2;-7;4) d(16;14;27). Показать, что векторы a b c образуют базис и н
Даны векторы а(2;7;3) b(3;1;8) с(2;-7;4) d(16;14;27). Показать, что векторы a b c образуют базис и найти координаты вектора d в этом базисе.
Все ответы
Даны векторы а(2;7;3) b(3;1;8) с(2;-7;4) d(16;14;27). Показать, что векторы a b c образуют базис и найти координаты вектора d в этом базисе.
Прямой ход метода Гаусса закончился, приступаем к обратному ходу.
Выбираем за ведущий элемент \(a_ <33>=1\),
умножим третью строку на 9 и сложим со второй строкой
$$= \left(\begin
Разделим строку 2 на 4, получаем
$$= \left(\begin
чтобы получить единичную матрицу осталось вычесть из первой строки вторую, умноженную на 5
$$= \left(\begin
и вычесть из первой строки третью строку, умноженную на 2
$$= \left(\begin
Ответ: координаты вектора \(d\) в базисе \((a;b;c)\) \(x =\left(\begin
Доказать, что векторы a, b, c образуют базис, найти координаты вектора d в этом базисе
Доказать, что векторы a, b, c образуют базис. Найти координаты вектора d в этом базисе.
Доказать что векторы a, b, c образуют базис и найти координаты вектора b в этом базисе
Доказать что векторы a, b, c образуют базис и найти координаты вектора d в этом базисе Помагите.
Покажите, что векторы e1 e2 e3 образуют базис и найдите координаты вектора x в этом базисе
В вещественном линейном пространстве в некотором базисе координаты векторов e1 e2 e3 x являются.
Доказать, что данные векторы образуют базис, и найти координаты вектора D
Даны векторы. a(10:3:1) b(1:4:2) c(3:9:2) d(19:30:7) показать что они образуют базис и найти.
Показать, что векторы образуют базис и найти в нем координаты данного вектора
Показать, что векторы a, b,c образуют базис и найти в нем координаты вектора m. а=(2;-2;1).
Если вы имеете в виду ортогональные проекции, то разве они не будут искомыми координатами только в ортонормированном базисе?
Проще всего делать, как сказано в сообщении 4. При этом доказательство базиса и взятие обратной матрицы можно делать одновременно, просто решая систему уравнений с расширенной матрицей (a b c | d) приведением к ступенчатому виду. Здесь я рассматриваю векторы a, b, c как столбцы. Вспомните, что если x1, x2, x3 — числа, то (a b c)(x1 x2 x3) T = x1*a + x2*b + x3*c.
Добавлено через 4 часа 1 минуту
разложить по 1-ому столбцу и выразить через 3 вектора
Iliodor, если вы пытаетесь оказать помощь, нельзя ли писать понятнее? Ясно ведь, что задача одна из самых первых по этой теме (базис и координаты) и что ТС плохо разбирается в этом. Может быть, они еще не проходили определители: они в этой задачи не нужны.
Что вы имеете в виду под определителем матрицы 4×3? Зачем его находить? Как это поможет выразить d через a, b, c? Если же рассмотреть матрицу, а не определитель, то что с ней делать? Приводить к ступенчатому виду элементарными преобразованиями строк? Но они не сохраняют линейную (не)зависимость строк. Последняя строка будет состоять из нулей, и как из этого найти коэффициенты разложения? Ведь рекомендация по решению уже написана в сообщении 6.