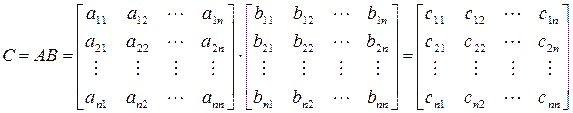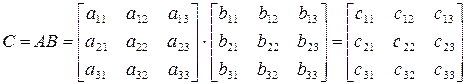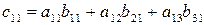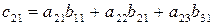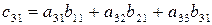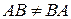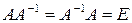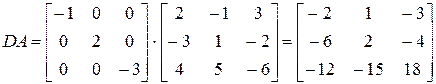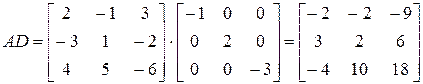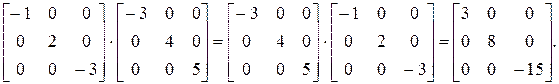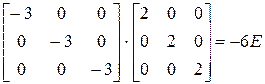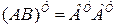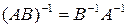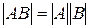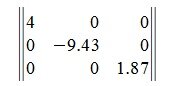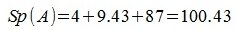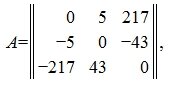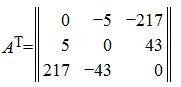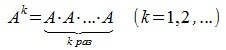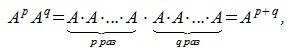Доказать что умножение матрицы а слева на диагональную матрицу b
Произведение матриц
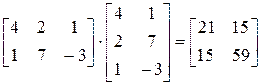
Под произведением двух матриц А и В понимается матрица С = АВ, элементы которой определяются путем умножения i-й строки первой матрицы на j-и столбец второй матрицы и полученные произведения складываются. Таким образом,
где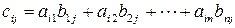 
, 
Процесс формирования произведения для быстрого запоминания можно облечь в следующую схему. Для иллюстрации рассмотрим перемножение двух матриц размерности 3×3.
Первая строка умножается на первый столбец. Результат перемножения складывается. Образуется элемент матрицы с11.
Вторая строка умножается на первый столбец. Результат перемножения складывается. Образуется второй элемент первого столбца с21.
Третья строка умножается на первый столбец. Результат умножения складывается, образуя последний элемент c31 первого столбца.
Операции по формированию элементов второго и третьего столбцов выполняются аналогично.
, 
, 
, 
, 
, 
.
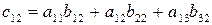
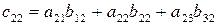
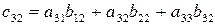
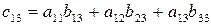
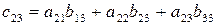
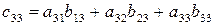
Обычная скалярная алгебра подчиняется шести с законам:
1) Закон коммутативности сложения:
.
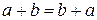
2) Закон ассоциативности сложения:
.
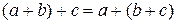
3) Закон коммутативности умножения:
.
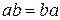
4) Закон ассоциативности умножения:
.
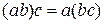
5) Закон дистрибутивности умножения:
, 
;
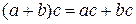
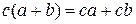
6) Неразложимость нуля на множители, отличные от нуля: если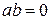 
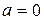
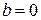
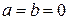
, то либо 
, либо 
, либо 
.
В операциях с матрицами законы 1, 2, 4 и 5 выполняются всегда. Однако законы 3 и 6 не соблюдаются. Закон 3 нарушается в силу того, что при перемножении матриц строки первой матрицы комбинируются со столбцами второй матрицы по изложенному выше правилу несимметрично. Такое несимметричное «перемешивание» элементов перемножаемых матриц между собой приводит к тому, что в общем случае
В тех случаях, когда операция умножения коммутативна, т. е.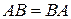 
, матрицы называются коммутативными (иногда коммутирующими) или перестановочными. Например, диагональные матрицы при умножении всегда коммутируют между собой, причем произведение диагональных матриц, в свою очередь, также является диагональной матрицей.
Скалярная матрица коммутирует с любой квадратной матрицей одинакового порядка. Это же свойство относится и к единичной матрице Е. Она выполняет такую же роль, как единица среди обычных скалярных величин:
, 
.
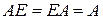
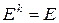
Кроме того, всегда соблюдается равенство
Каждая матрица коммутирует сама с собой и со своей произвольной целой положительной степенью.
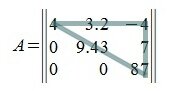
Пример 4.1. Умножение матрицы А слева на диагональную матрицу D эквивалентно умножению каждой строки матрицы А на соответствующий диагональный элемент:
Пример 4.2. Умножение справа на D сводится к умножению элементов каждого столбца на соответствующий элемент диагонали:
Пример 4.3. Коммутируемость диагональных матриц:
Скалярная матрица (матрица, у которой диагональные элементы равны между собой) равна произведению единичной матрицы на скалярную величину. В качестве примера перемножим две скалярные матрицы:
Справедливо следующее правило транспонирования произведения. Транспонированное произведение матриц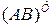 
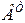
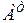
равно произведению двух транспонированных матриц 
и 
, перемноженных в обратной последовательности:
Произведение любой матрицы на свою транспонированную является симметрической матрицей. Например,
Произведение обратных матриц подчиняется тому же свойству перестановки сомножителей, что и произведение транспонированных матриц, а именно
Определитель произведения двух квадратных матриц равен произведению определителей перемножаемых матриц:
При образовании произведения нескольких матриц множители в силу ассоциативности закона умножения можно группировать как угодно, при условии, что порядок перемножения сомножителей не нарушается.
При умножении матрицы ранга r на неособенную справа или слева ранг произведения остается равным r.
Дата добавления: 2014-12-27 ; просмотров: 5327 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Доказать что умножение матрицы а слева на диагональную матрицу b
Например, диагональная матрица не изменится, если ее строки объявить столбцами (при этом ее столбцы автоматически становятся строками). Поэтому для диагональных матриц A и B исчезает неравноправие между строками и столбцами в произведении таких матриц и, следовательно, AB = BA.
У каждого элемента, расположенного на главной диагонали квадратной матрицы, номер строки совпадает с номером столбца. Все другие матричные элементы a i j (i ≠ j) диагональной матрицы A равны нулю.
Подобные ситуации встречаются достаточно часто и поэтому договорились использовать для их описания специально введенное выражение вида δ i j :
Вот примерно такова логика изложения в данном разделе!
 | (1) |
Совокупность элементов, расположенных на диагонали, проходящей из правого верхнего угла в левый нижний угол, называется побочной диагональю.
Матрица 
, все внедиагональные элементы которой равны нулю, называется диагональной. Другими словами, элементы диагональной матрицы удовлетворяют условиям
 | (2) |
Для записи подобных выражений удобно использовать дельта-символ Кронекера, определяемый формулой
 | (3) |
Очевидно, что дельта-символ симметричен относительно перестановки индексов:
Другое важное свойство дельта-символа δi j заключается в том, что он снимает суммирование в выражениях вида
Диагональная квадратная матрица с равными диагональными элементами называется скалярной.
Описание файла
Просмотр DJVU-файла онлайн
Найти е’,Ае, если А = (а; ) е К «», а е’, и е — единичные строка и столбец подходящих размеров. 1.14. Мапгричной единицей Е, размера т х и называется матрица, у которой элемент в позиции (г, г) равен единице, а все остальные элементы равны нулю. Для произвольной матрицы А и матричной единицы Е,б подходящего размера вычислить: а) АЕеб б) Е, А. 1.15. Найти ДА): а) Д
х) = хг — 2х+ 2, А = б)
6 2) произведение А
6 Глава 1. Матрицы 1.16. Доказать, что каждая квадратная матрица второго по-
с х — (а+ а1)х+ (ай — бс) = О. 1.17. Доказать, что если А — диагональная матрица, то матрица ДА) также диагональная, каков бы ни был многочлен Дх). 1.18. Вычислить: а) ; б) — 2 — 4 0 1.19.
Вычислить а),; б) д) 1 О,п>2; е) ) О Л ‘ ) О 1 спаса — в1па 1 в1па спаса
= (А+ В)(А — В). 1.24. Доказать, что если матрицы А и В перестановочны, то: а) 4з+ Вз (4+ ВИАз 4В+ Вз). б) (А+ В) А +С,’,А22-
В + + В 1.25. Найти п-ю степень матрицы А, если матрица А равна: 6)
— 4 — 5 10 11 Аа Азв 1.26. В ычислить матрицу + + + +, если матрица А равна:
— 2 — 21′ )[ а) 2 2,’ б) 1.27. Найти все если: )А=
— 2 — 21 матрицы, перестановочные с матрицей А, б)А= 2 1, в)А= 0100 0010 0001 г) А= 0000 ) А — квадратна е я матрица и-го порядка, все элементы которой равны единице. 1.28. Доказать, что умножение матрицы А слева на диагональную матрицу 1А’ = 222а81Лц Лз. Л„) равносильно умноже- )А= [ б) А= 1010’с2 — 1о — 1’23 с2 — 1 22 ‘ — 10 — 9 д) А — матричная единица В2.
Е 222″ 22; Глава 1. Матрицы нию строк А соответственно на Лы Лз. Л„, умножение же А на Р справа равносильно аналогичному изменению столбцов. 1.29. Найти матрицу А, если И,’И 2 5 А= 1.30. Доказать, что если А — диагональная матрица и все элементы ее главной диагонали различны между собой, то любая матрица, перестановочная с А, также диагональна. 1.31. Доказать, что квадратная матрица А перестановочна со всеми диагональными матрицами тогда и только тогда, когда она сама является диагональной. 1.32.
Доказать, что квадратная матрица А перестановочна со всеми квадратными матрицами того же порядка тогда и только тогда, когда она является скалярной. 1.33. Доказать, что если матрица А перестановочна с матрицей В, то она перестановочна и с матрицей В
. Верно ли обратное? 1.34. Пусть А — квадратная матрица и 1(х) и д(х) — произвольные многочлены. Показать, что матрицы 1(А) и д(А) перестановочны.
1.35. Доказать, что след матрицы обладает следующими свойствами: а) сг(А+ В) = сгА+ сгВ; б) сг(аА) = асгА; в) сг(Ат) = сгА; г) сг(АВ) = сг(ВА), если произведения АВ, ВА определены. 1.36. Доказать, что для любой матрицы величина Сг(АтА) неотрицательна, причем равна нулю тогда и только тогда, когда матрица А нулевая. 1.36.1. Существуют ли матрицы А и В, для которых равенство АХВ = Х
выполняется при любой матрице Х б К
«»? 1.36.2. Можно ли свести операцию транспонирования матрицы общего вида к операциям умножения ее слева и справа на какие-либо наперед заданные матрицы? 1.37.
Доказать, что для любых квадратных матриц А и В одинакового размера их коммутатор [А, В] имеет нулевой след. 1.38. Доказать, что равенство [А, В] = 1 не выполнено ни для каких вещественных матриц А и В. 19 з1. Операции над матрицами и [аб) Е К'»»» величина т, =
си 1=1 т суммой, а величина с =
=1 1.39. Для матрицы А = называется ее г-й стпрочной
-й столбцовой суммой. а) Показать, что т
Считая, что произведение АВ определено, доказать, что все строчные суммы в АВ также одинаковы и равны ар’. в) Сформулировать и доказать столбцовый вариант утверждения пункта «б». 1.40. Доказать, что если квадратные матрицы А и В порядка и таковы, что для любого вектор-столбца С Е К»»
выполнено соотношение Ас = Вс, то А = В. 1.41.
Доказать, что если квадратные матрицы А и В порядка и таковы, что для любых вектор-столбцов С, и Е К»»» выполнено соотношение с,
Ви, то А = В. 1.42. Найти коммутатор матричных единиц Е, и Еы и показать, что он нулевой тогда и только тогда, когда либо г = у = 1с = 1, либо [1 — 1с) [1 — 1) ф О. 1.43. Доказать, что диагональная матрица с нулевым следом является линейной комбинацией коммутаторов матричных единиц. 1.44. Показать, что коммутатор обладает следующими свойствами: Глава 1, Матрицы 20 1.45. Доказать,что равенство [[А, В],С] = [А, [В,С)] выполнено тогда и только тогда, когда матрицы [А, С] и В пере- становочны.
1.46. Доказать, что для любых матриц А, В, С второго по- рядка выполнено соотношение [[[А, В]) г, С] = О. 1.47. Доказать, что любая матрица с нулевым следом явля- ется суммой коммутаторов матриц с нулевым следом. 1.48. Доказать, что для любой матрицы А с нулевой глав- ной диагональю найдутся матрица Х и диагональная матрица Р такая, что [Х, Р) = А. 1.49. Произведениелл Йордана А в В квадратных матриц А и В одного порядка называется матрица 1[АВ + ВА). Показать, что произведение Иордана обладает следующими свойствами: а) А*В = В в А; б) [сгА) в В = сгА * В; в) [А+В) е С= А*С+В*С; г) А*А = Аг; д) А*1=А; В)т Ат „Вт, ж) [Аг в В) * А = Аг * [В* А), выполненными для любых квадратных матриц А, В, С и еди- ничной матрицы 1 одного порядка.
2.2. Найти количество операций умножения, необходимых для вычисления произведения двух треугольных матриц порядка и одного вида. 2.3. Пусть А = (а,у) — треугольная матрица и-го порядка и »с Е (Ч. Найти йг А». 2.4. Доказать, что для любой треугольной матрицы А с положительными диагональными элементами найдется треугольная матрица В того же вида с положительными диагональными элементами такая, что В
, то произведению АВ соответствует блочная матрица С = (Сс ) с элементами з Ссс =
АссВсг. с=с 2.8. Применяя описанное в предыдущей задаче правило умножения блочных матриц, вычислить й— ‘[4— б) [ — 1 — 1 — 2 — 1 0 0 100 011 001 — 2 в)012 110 1;г)202 — 110 ной.
2.6. Квадратная матрица А порядка п.называется ленпсочной, если для некоторого числа т (меньшего и — 1) все элементы а; с индексами, удовлетворяющими условию
с — Я ) т, равны нулю. Число 2т+ 1 называется шириной ленты. Найти ширину ленты произведения ленточных матриц, если для сомножителей эта ширина равна 2псс + 1, 2тг + 1 соответственно и тс + тг
Матрицы. Виды матриц
Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.
Матрица порядка m × n записывается в форме:
или 
(i=1,2. m; j=1,2. n).
Числа aij входящие в состав данной матрицы называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j— номер столбца.
Матрица строка
Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:
Матрица столбец
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например
Нулевая матрица
Квадратная матрица
Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:
Главная диагональ матрицы
Побочная диагональ матрицы
Диагональная матрица
Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:
Единичная матрица
След матрицы
Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:
Верхняя треугольная матрица
Нижняя треугольная матрица
Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. aij=0, при всех i T ).
Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).
Ядро или нуль пространство матрицы
Противоположная матрица
Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.
Кососимметричная (Кососимметрическая) матрица
Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:
В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.
Пример кососимметрической матрицы:
Разность матриц
Разностью C двух матриц A и B одинакового размера определяется равенством
Для обозначения разности двух матриц используется запись:
Степень матрицы
Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:
где E-единичная матрица.
Из сочетательного свойства умножения следует:
где p,q— произвольные целые неотрицательные числа.
Симметричная (Симметрическая) матрица
Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.
Для симметричных матриц имеет место равенство:
Математика для чайников. Матрицы и основные действия над ними
Определение матрицы
Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.
Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.
Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.
Операции сложения и вычитания матриц
Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.
Вычитание выполняется по аналогии, только с противоположным знаком.
Умножение матрицы на число
На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:
Операция умножения матриц
И пример с реальными числами. Умножим матрицы:
Операция транспонирования матрицы
Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:
Определитель матрицы
Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!
Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
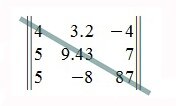
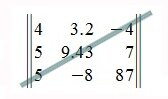
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.
Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.
А если матрица три на три? Тут уже посложнее, но справиться можно.
Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.
К счастью, вычислять определители матриц больших размеров на практике приходится редко.