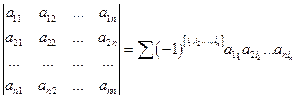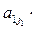Доказать что в группе sn порядок нечетной перестановки является четным числом

05. Определители. Перестановки и их четность

1. Бугров Я. С., Никольский С. М. Элементы линейной алгебры и аналитической геометрии. 1997, с. 7-22.

3. Кремер Н. Ш. Высшая математика для экономистов. М.: Юнити, 2000. с. 16-26.

4. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1980, с. 148-156.

различные элементы N-элементного множества M.

Теорема 1.Число всех перестановок из n различных элементов равно .

Число всех инверсий в перестановок обозначаем символом .

Определение 3. Перестановка называется Четной, если число всех инверсий в перестановке четное, перестановка называется Нечетной, если число всех инверсий в перестановке нечетное.

Пример 3. Для N=2 имеется 6 перестановок. При этом три перестановки (1,2,3), (3,1,2), (2,3,1) четные и три перестановки (1,3,2), (2,1,3), (3,2,1) нечетные.

Определение 4. Транспозицией Перестановки называется такое ее преобразование при, при котором два ее элемента переставляются местами, а остальные остаются на своих местах.

Теорема 2. При любой транспозиции перестановки ее четность меняется на противоположную.

Доказательство. Рассмотрим два случая.

Доказательство. Пусть и соответственно число всех четных и нечетных перестановок. Пусть любая из четных перестановка. Проводя в них транспозиции первых двух элементов , получим Различных нечетных перестановок. Так как всего нечетных перестановок , то . Проводя аналогичное рассуждение с нечетными перестановками получим . Из этих двух неравенств следует, что =. Теорема доказана.

Следствие. При N>1 Число всех четных перестановок равно .

Источник

Перестановки 4 элементов

Знак перестановки можно явно выразить как

В качестве альтернативы знак перестановки σ может быть определен из ее разложения на произведение транспозиций как

СОДЕРЖАНИЕ

Пример

Есть много других способов записать σ как композицию транспозиций, например

но записать это как произведение четного числа транспозиций невозможно.

Характеристики

Следующие правила прямо вытекают из соответствующих правил сложения целых чисел:

Из этого следует, что

На практике, чтобы определить, является ли данная перестановка четной или нечетной, ее записывают как произведение непересекающихся циклов. Перестановка нечетная тогда и только тогда, когда эта факторизация содержит нечетное количество циклов четной длины.

Другой метод определения, является ли данная перестановка четной или нечетной, состоит в построении соответствующей матрицы перестановок и вычислении ее определителя. Значение определителя такое же, как четность перестановки.

Каждая перестановка нечетного порядка должна быть четной. Перестановка (1 2) (3 4) в A ₄ показывает, что в общем случае обратное неверно.

Эквивалентность двух определений

В этом разделе представлены доказательства того, что четность перестановки σ может быть определена двумя эквивалентными способами:

Любую перестановку можно записать как произведение нечетного числа перестановок соседних элементов, например

(2 5) = (2 3) (3 4) (4 5) (4 3) (3 2).

Таким образом, мы можем определить четность σ как четность его составных транспозиций в любом разложении. И это должно согласовываться с четностью числа инверсий при любом порядке, как показано выше. Следовательно, определения действительно четко определены и эквивалентны.

Альтернативное доказательство использует полином Вандермонда

Так, например, в случае n = 3 мы имеем

Обратите внимание, что изначально, когда своп не применяется, количество инверсий равно 0. Теперь мы получаем эквивалентность двух определений четности перестановки.

Рассмотрим элементы, зажатые между двумя элементами транспозиции. Каждый из них находится полностью вверху, полностью вверху, полностью внизу или между двумя элементами транспозиции.

Другие определения и доказательства

п минус количество непересекающихся циклов в разложении σ <\ displaystyle n <\ text <минус количество непересекающихся циклов в разложении>> \ sigma>

если мы позаботимся включить неподвижные точки σ как 1-циклы.

и если a и b находятся в одном цикле σ, то

Обобщения

Четность может быть обобщена на группы Кокстера : определяется функция длины ℓ ( v ), которая зависит от выбора образующих (для симметрической группы, смежных транспозиций ), а затем функция v ↦ (−1) ℓ ( v ) дает обобщенная карта знаков.

Источник

Перестановки и транспозиции, определители

Дата добавления: 2015-07-23 ; просмотров: 5050 ; Нарушение авторских прав

В множестве из п чисел общее количество перестановок равно п!.

Говорят, что в данной перестановке числа i, j образуют инверсию, если i> j, но i стоит в перестановке раньше j.

Например, перестановка 15243. Числа 5, 2 образуют инверсию.

Например 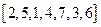=2+0+3+1+0+1=7

Перестановка называется четной, если ее числа состав­ляют четное количество инверсий, и нечетной — в противном случае.

Транспозициейназывается преобразование перестановки, при котором меняются местами какие-либо два числа, не обяза­тельно стоящие рядом.

Теорема 4.1 Всякая транспозиция меняет четность перестановки.

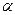
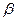
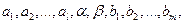
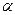
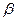
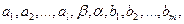
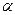
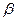
□ Рассмотрим сначала случай, когда меняются местами два соседних элемента и перестановки После транспозиции элементов и получим переста­новку Так как перестановки отличаются друг от друга только взаимным расположением элементов и (а взаимное расположение каждого из этих элемен­тов и какого-то другого, так же как и взаимное располо­жение любых двух из остальных элементов, остались прежними), то число инверсий в второй перестановке на единицу больше или на единицу меньше числа инвер­сий в первой перестановке, и значит, одна из этих пере­становок четная, а другая — нечетная.

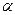
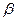
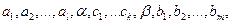
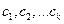
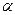
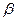
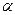
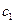
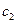
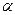
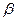
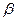
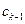
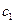
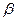
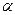
Общий случай. Пусть меняются местами элементы и перестановки между которыми стоят еще k элементов . Можно выполнить транспозицию элементов и посредством нескольких транспозиций рядом стоящих элементов: поменяем местами сначала с , затем с и т. д., наконец, с c_k (при этом сделаем k транс­позиций рядом стоящих элементов); затем поменяем местами и (еще одна транспозиция) и, наконец, поменяем местами последовательно с , с и так далее, до (еще k транспозиций рядом стоящих элементов). В итоге станет на место и наоборот. При каждой такой транспозиции четность перестановки меняется. Так как она изменит­ся нечетное число раз (2k + 1), поэтому не­четная перестановка сделается четной, а четная — не­четной.■

Следствие. Число четных перестановок равно числу нечетных и равно 0,5 n!

□ Пусть из n! перестановок из n элементов p перестановок четные и q нечетные. Сдела­ем в каждой четной перестановке одну и ту же транс­позицию, например, поменяем местами первые два эле­мента. Тогда каждая четная перестановка превратится в нечетную, при этом все p полученных при этом нечетных перестановок будут разными. А так как общее число нечетных перестановок из n элемен­тов, по предположению, равно q, то p р. Следова­тельно, p = q.!

Все n! перестановок из n чисел можно расположить в таком порядке, что каждая следующая будет получаться из пре­дыдущей при помощи одной транспозиции, причем начинать мож­но с любой перестановки.

Определителем n-го порядка, соответствующим квадрат­ной матрице порядка n, называется алгебраическая сумма n! членов, составленная следующим образом. Членами определителя служат всевозможные произведения по n элементов матрицы, взятых по одному в каждой строке и каждом столбце. Член бе­рется со знаком плюс, если индексы столбцов его элементов об­разуют четную перестановку при условии, что сами элементы расположены в порядке возрастания номеров строк, и со знаком минус — в противном случае и обозначается:

= det A =

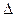
Определителем первого порядка является величина элемента :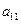

.

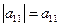
Определителем второго порядка равен произведению элементов на главной диагонали минус произведение элементов на побочной диагонали:

.

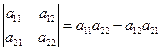
Определитель третьего порядка, вычисленный по правилу Саррюса

Источник

Линейная Алгебра

Чётность перестановки

Теорема. Любая транспозиция соседних элементов перестановки меняет четность перестановки на противоположную.

Доказательство. Пусть дана перестановка , в которой мы выполним транспозицию (i j) и получим перестановку . Сразу заметим, что все пары, которые образовывали инверсию в старой перестановке, образуют инверсию и в новой, кроме возможно одной пары: (i, j). Если эта пара давала инверсию в старой перестановке, то в новой уже нет и число инверсий уменьшается на 1. Если же эта пара не образовывала инверсию в старой перестановке, то в новой образует инверсию и число инверсий увеличивается на 1. В любом случае, число инверсий изменяется на 1, а следовательно, меняется четность перестановки.

Теорема. Любая транспозиция любых двух элементов перестановки меняет четность перестановки на противоположную.

Доказательство. Пусть выполняется транспозицию (i j) и пусть между элементами i и j находится m других элементов. Легко видеть, что такую транспозицию можно выполнить за транспозицию соседних элементов, откуда и следует теорема.

Теорема. Любую перестановку можно получить из начальной перестановки последовательным выполнением конечного числа транспозиций, причем это количество транспозиций есть число четное, если данная перестановка четна, и нечетное в противном случае.

Доказательство. Очевидно в свете следующего примера.

Пример.

.

Здесь, перестановка приведена к начальной за

4 транспозиции и она четная, т.к. .

Замечание. Понятно, что любую перестановку можно привести к начальной и обратно с помощью тех же самых транспозиций, выполненных в обратном порядке.

Теорема. Количество четных перестановок множества из элементов равно количеству нечетных и равно .

Доказательство. Каждая перестановка либо четная, либо нечетная. Поэтому общее количество четных перестановок неизменно. Так же и количество нечетных перестановок есть число фиксированное. Во всех перестановках выполним одну и ту же транспозицию, например, (1 2). Все четные перестановки станут нечетными и наоборот, все нечетные станут четными. Следовательно, четных и нечетных перестановок одинаковое количество.

Замечание. Предлагается следующая интерпретация к предыдущей теореме.

Пусть на некоторой вечеринке находится какое-то количество людей, причем все женщины в шляпках, а мужчины в масках. Допустим, что в некоторый момент времени, каждый мужчина должен отдать женщине свою маску и получить от нее головной убор. Каково должно быть соотношение мужчин и женщин, чтобы каждый мужчина получил шляпку, а каждая женщина – маску?

Источник

Перестановки n-й степени. Теорема о четности перестановки. Определители n-го порядка. Определители второго и третьего порядков

Определение 1. Пусть М=<1,2,…,n>. Перестановкой на множестве М или перестановкой n-й степени называется множество М с заданным расположением его элементов, и обозначается I=(i₁i₂…i_n), где i₁,i₂. i_n – попарно различные элементы из М.

Определение 2. Инверсией или беспорядком перестановки I называется любая пара символов перестановки I, в которой символ, стоящий левее, больше символа, стоящего правее.

Пример 2. В перестановке I₂=(231) две инверсии: 31 и 21.

Через s(I) будем обозначать число всех инверсий перестановки I.

Определение 3. Перестановка I называется чётной, если s(I) – чётное число, в противном случае перестановка I называется нечётной.

В примере 2 перестановка I – чётная.

Через S_n обозначается множество всех перестановок n-ой степени. Можно доказать, что количество всех перестановок из n элементов равно n!=1×2×3×…×n. Например, из 3 элементов можно составить 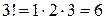перестановок. Это будут 123, 132, 231, 321, 312, 231.

Определение 4.Транспозицией называется перемена местами 2-х элементов перестановки, когда остальные элементы остаются на месте.

Теорема 1. Транспозиция меняет четность перестановки. Другими словами, четность перестановки изменится, если в ней поменять местами два произвольных символа.

Пусть А=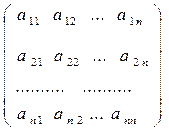— матрица n-го порядка над полем Р.

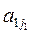
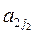
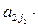
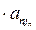
Из элементов матрицы А будем составлять всевозможные произведения, состоящие из n множителей, любые два различных из которых находятся в разных строках и разных столбцах. Таким, например, является произведение элементов, стоящих на главной диагонали: a₁₁a₂₂…a_nn. Все такие произведения можно получить по следующему правилу: выберем для произведения из первой строки матрицы А некоторый элемент , затем вычеркнем первую строку и j₁-й столбец, и в полученной подматрице из первой строки выбираем некоторый элемент и т.д. Через конечное число шагов получим произведение вида: ….

Так как j₁,j₂,…,j_n – попарно различные элементы из множества М=<1,2,…,n>, то вторые индексы в записанном произведении образуют перестановку I=(j₁j₂…j_n).

Рассмотрим выражение вида: (-1) s ( I ) 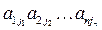(1), где I=(j₁j₂…j_n).

Выражений вида (1) можно образовать столько, сколько существует перестановок, составленных из вторых индексов, т.е. их будет n!.

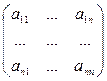
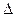
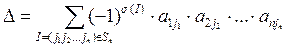
Определение 5. Пусть А=— матрица n-го порядка над полем Р. Определителем матрицы А (или, коротко, определителем n-го порядка) называется элемент поля Р, равный .

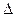
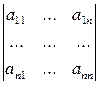
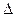
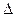
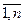
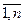
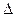
Используются следующие обозначения: =, =|A|, =|a_ij|, i=, j=,

=det A.

1) Пусть Δ – определитель 2-го порядка, т.е. Δ ==.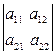

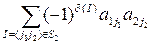
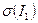
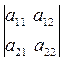
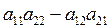
Так как I₁ = (12) и = 0, то получим Δ = = .

Таким образом, определитель 2-го порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной диагонали.

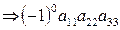
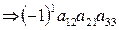
I₁ = (123) = 0 ; I₂ = (213) = 1 ;

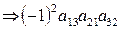
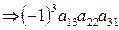
I₃ = (312) = 2 ; I₄ = (321) = 3 ;

I₅ = (132) = 1 ;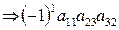

I₆ = (231) = 2 .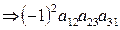

Δ== .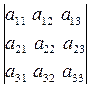

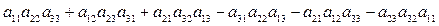
Таким образом, определитель 3-го порядка равен сумме шести слагаемых, три из которых со знаком +.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник