Доказать что в нетривиальном графе существуют вершины одинаковой степени
Доказать, что в любом графе, имеющем хотя бы одно ребро, найдутся две вершины одинаковой степени
2) Доказать, что в любом графе, имеющем хотя бы одно ребро, найдутся две вершины одинаковой степени.
У меня пока туго с графами, я пытаюсь разбираться. Заранее спасибо
Добавлено через 20 минут
Разобрался, через степень 0 и 1, что не может быть такого
Доказать,что в любом графе с n вершинами есть минимум две вершины с одинаковой степенью
Помогите пожалуйста доказать,что в любом графе с n вершинами есть минимум две вершины с одинаковой.
Найти раскраску вершин графа минимальным числом цветов так, что ни одно ребро не соединяло две вершины одного цвета
Найти раскраску вершин графа минимальным числом цветов так, что ни одно ребро не соединяло две.
Матрица инцидентности орграфа, когда две вершины взаимодостижимы через одно ребро
К примеру, матрица смежности: Как в этом случае заполнять матрицу инцидентности? Ведь вершина.

Есть очень интересная задачка про принцип Дирихле В клетках шахматной доски 100х100 записаны.
Покажите, что в любом графе количество вершин нечетной степени четно.
Покажите, что в любом графе количество вершин нечетной степени четно.

формулу или объяснить на примере
Доказать, что 7 в степени n умножить на 2 в степени 3k минус 2 в степени 2k кратное 47
Доказать что 7 в степени n умножить на 2 в степени 3k минус 2 в степени 2k кратное 47 Для набора.
Как определить, связны ли две вершины в графе?
Доброго времени суток! Подскажите пожалуйста алгоритм, который смог бы определить, связны ли две.
Пояснения к доказательству
Доказательство
Пусть дан (n,m)-граф G. Предположим противное: все его вершины имеют разную степень.
Максимальная степень вершины в графе порядка n может быть равна (n-1), тогда вершины должны иметь степени (n-1), (n-2), …, 2, 1, 0. Но вершина степени (n-1) соединена со всеми оставшимися вершинами, в том числе и с изолированной, что невозможно. Пришли к противоречию, поэтому в любом графе обязательно найдутся две вершины, имеющие одинаковую степень. максимальная степень вершины может быть на единицу меньше количества вершин.
1.3 Теорема о вершинах степени 0 или n-1
Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента aij равно числу рёбер из i-й вершины графа в j-ю вершину.
Иногда, особенно в случае неориентированного графа, петля (ребро из i-й вершины в саму себя) считается за два ребра, то есть значение диагонального элемента aii в этом случае равно удвоенному числу петель вокруг i-й вершины.
Матрица смежности простого графа (не содержащего петель и кратных рёбер) является бинарной матрицей и содержит нули на главной диагонали.
Операции с графами
Гомеоморфизм графов ответ находится выше.
3.3 Теорема о связности дополнения графа
Для любого графа либо он сам, либо его дополнение – связный граф.
Доказательство
Возьмем произвольный граф 




Если вершины 



Если вершины 




3.4 Теорема о простом цикле.
Выберем в графе минимальный по количеству рёбер цикл (он существует, потому что количество рёбер в любом цикле — натуральное число [1] ). Предположим, что он не простой. Но тогда он содержит дважды одну и ту же вершину, т. е. содержит в себе цикл меньшего размера, что противоречит тому, что наш цикл минимальный. Таким образом, этот цикл — простой.
3.5 Признаки двудольности графа
2) Граф разбивается на пары разноцветных вершин тогда и только тогда, когда любые k элементов одной из долей связаны по крайней мере с k элементами другой(Теорема о свадьбах)
| Доказательство: |
 |
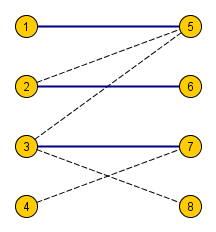
 Очевидно, что если существует полное паросочетание, то для любого Очевидно, что если существует полное паросочетание, то для любого  выполнено выполнено  . У любого подмножества вершин есть по крайней мере столько же соседей (соседи по паросочетанию). . У любого подмножества вершин есть по крайней мере столько же соседей (соседи по паросочетанию).  В обратную сторону докажем по индукции (будем добавлять в изначально пустое паросочетание В обратную сторону докажем по индукции (будем добавлять в изначально пустое паросочетание  по одному ребру и доказывать, что мы можем это сделать, если по одному ребру и доказывать, что мы можем это сделать, если  не полное). Таким образом, в конце получим что не полное). Таким образом, в конце получим что  — полное паросочетание. База индукции Вершина из — полное паросочетание. База индукции Вершина из  соединена хотя бы с одной вершиной из соединена хотя бы с одной вершиной из  . Следовательно база верна. Индукционный переход Пусть после . Следовательно база верна. Индукционный переход Пусть после  шагов построено паросочетание шагов построено паросочетание  . Докажем, что в . Докажем, что в  можно добавить вершину можно добавить вершину  из из  , не насыщенную паросочетанием , не насыщенную паросочетанием  . Рассмотрим множество вершин . Рассмотрим множество вершин  — все вершины, достижимые из — все вершины, достижимые из  , если можно ходить из , если можно ходить из  в в  только по ребрам из только по ребрам из  , а из , а из  в в  по любым ребрам из по любым ребрам из  . Тогда в . Тогда в  найдется вершина найдется вершина  из из  , не насыщенная паросочетанием , не насыщенная паросочетанием  , иначе, если рассмотреть вершины , иначе, если рассмотреть вершины  (вершины из (вершины из  принадлежащие принадлежащие  ), то для них не будет выполнено условие: ), то для них не будет выполнено условие:  . Тогда существует путь из . Тогда существует путь из  в в  , который будет удлиняющим для паросочетания , который будет удлиняющим для паросочетания  (т.к из (т.к из  в в  мы проходили по ребрам паросочетания мы проходили по ребрам паросочетания  ). Увеличив паросочетание ). Увеличив паросочетание  вдоль этого пути, получаем искомое паросочетание. Следовательно предположение индукции верно. вдоль этого пути, получаем искомое паросочетание. Следовательно предположение индукции верно. |
Пояснения к доказательству
Пусть было построено паросочетание размером 
Добавляем вершину с номером 
Во множество 




Ненасыщенная вершина из правой доли всегда найдется (в примере вершина с номером 
Цепь 
Увеличив текущее парасочетание вдоль этой цепи, мы насытим вершину с номером 
3) Граф является двудольным тогда и только тогда, когда он 2-раскрашиваем; то есть его хроматическое число равняется двум.
3.6 Распознование двудуульности поиском в ширину.
Деревья
4.1 Признаки дерева.
1) Отсутствие циклов
2) Любые две вершины соединяет простая цепь.(единственная)
4.3 Три способа построения остова, обход графа в глубину.
4.4 Фундаментальные циклы.
4.5 Теорема о центре дерева.
4.6 Теорема Кирхгофа о числе остовов
4.9 Поиск Остова минимального веса. Алгоритм Краскала
4.10 Поиск Остова минимального веса Алгоритм Прима
4.11 Матричный Алгоритм Прима. Приведён выше J
Связность
Теорема о точках сочленения.
5.3 Теорема о связи чисел вершинной и рёберной связности
Для любого графа 

5.5 Теоремы о блоках графа
Теорема 1. Два различных блока одного графа могут иметь не более одной общей вершины. Вершина принадлежит более чем одному блоку тогда и только тогда, когда она является шарниром графа.
Если вершина 
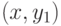










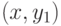

6.1 Теорема Эйлера о связи чисел, вершин, рёбер и граней.
6.2 Непланарность графов К5 К3,3
Заметим, что из планарности графа следует планарность гомеоморфного графа и наоборот. В самом деле, пусть 






Докажем неоходимость. От противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных 


Теорема Фари Для любого планарного графа существует плоское представление в котором все рёбра прямолинейные отрезки.
| Доказательство: |
 |
Докажем теорему для плоской триангуляции графа  . Ее можно достичь, добавив в . Ее можно достичь, добавив в  необходимое количество ребер. Применим индукцию по числу вершин необходимое количество ребер. Применим индукцию по числу вершин 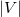 . База индукции, когда . База индукции, когда  , выполняется тривиальным образом. Предположим, что графы с любым числом вершин меньше , выполняется тривиальным образом. Предположим, что графы с любым числом вершин меньше 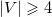 , мы можем нарисовать требуемым образом. Рассмотрим ребро , мы можем нарисовать требуемым образом. Рассмотрим ребро  , инцидентное внутренней вершине глубочайшего разделяющего треугольника, то есть такого, который не содержит внутри себя других разделяющих треугольников. Если в графе нет разделяющих треугольников, то возьмём любое ребро. Тогда , инцидентное внутренней вершине глубочайшего разделяющего треугольника, то есть такого, который не содержит внутри себя других разделяющих треугольников. Если в графе нет разделяющих треугольников, то возьмём любое ребро. Тогда  — граница двух граней — граница двух граней  и и  . .  Так как мы взяли вершины внутри самого глубого разделяющего треугольника, то у вершин Так как мы взяли вершины внутри самого глубого разделяющего треугольника, то у вершин  и и 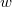 может быть только два общих соседа может быть только два общих соседа 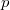 и и  . Пусть . Пусть 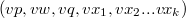 и и 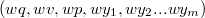 — обход по часовой стрелке ребер, исходящих соостветсвенно из — обход по часовой стрелке ребер, исходящих соостветсвенно из  и и 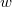 . Пусть . Пусть  — граф, полученный из — граф, полученный из  стягиванием ребра стягиванием ребра  в вершину в вершину  . Заменим пары параллельных ребер . Заменим пары параллельных ребер 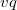 и и  на на  и и  на на  . Получим вершину . Получим вершину  , из которой исходят ребра , из которой исходят ребра  — по часовой стрелке. — по часовой стрелке.  Мы получили граф Мы получили граф  , с меньшим числом вершин равным , с меньшим числом вершин равным 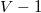 , то есть его можно уложить на плоскости требуемым образом: все ребра прямые (и сохранен обход по часовой стрелке ребер, инцидентных , то есть его можно уложить на плоскости требуемым образом: все ребра прямые (и сохранен обход по часовой стрелке ребер, инцидентных  ). Для любого ). Для любого  обозначим обозначим  — круг радиуса — круг радиуса  , с вершиной , с вершиной  в центре. Для каждого соседа в центре. Для каждого соседа  вершины вершины  в графе в графе  обозначим обозначим  объединение всех отрезков, проведённых из объединение всех отрезков, проведённых из  в в  . Возьмем . Возьмем  равным минимуму из всех расстояний от вершины равным минимуму из всех расстояний от вершины  до инцидентных ей вершин и до отрезков, проходящих мимо нее. до инцидентных ей вершин и до отрезков, проходящих мимо нее.  Тогда получим, что все соседи Тогда получим, что все соседи  вершины вершины  находятся снаружи находятся снаружи  и только ребра и только ребра  , инцидентные , инцидентные  , могут пересекать , могут пересекать  . . 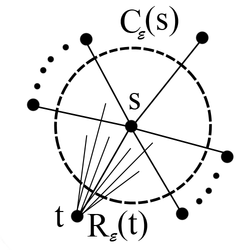 Проведем линию Проведем линию  через вершину через вершину  так, чтобы вершина так, чтобы вершина 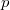 лежала с одной ее стороны, а лежала с одной ее стороны, а  — с другой (такая линия существует, иначе рёбра — с другой (такая линия существует, иначе рёбра  и и  накладывались бы друг на друга) и никакое из ребер накладывались бы друг на друга) и никакое из ребер  и и  не лежало на не лежало на  . Ребра . Ребра  и и  разбивают разбивают  на две дуги: первая пересекает ребра на две дуги: первая пересекает ребра  , а вторая — ребра , а вторая — ребра  . .  пересекает пересекает  в двух точках. Расположим в двух точках. Расположим  и и 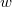 в этих точках: в этих точках:  на дуге, пересекающей на дуге, пересекающей  , а , а 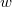 с другой стороны. с другой стороны.  Удалим Удалим  и инцидентные ей ребра, нарисуем прямые ребра и инцидентные ей ребра, нарисуем прямые ребра  , инцидентные , инцидентные  и и 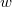 . .  Получим, что Получим, что  лежит на лежит на  . Так как . Так как 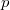 и и  лежат с разных сторон лежат с разных сторон  , ребра, инцидентные , ребра, инцидентные  и и 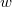 , не пересекаются. По выбору , не пересекаются. По выбору  , ребра, инцидентные , ребра, инцидентные  и и 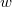 , не пересекают и другие ребра , не пересекают и другие ребра  . Таким образом желаемая укладка графа . Таким образом желаемая укладка графа  достигнута. Теперь мы можем удалить добавленные нами ребра, оставив в графе лишь исходные (уже прямые) ребра. достигнута. Теперь мы можем удалить добавленные нами ребра, оставив в графе лишь исходные (уже прямые) ребра. |
6.5 Гамма Алгоритм укладки графа на плоскости
Обходы в Графах
7.1 Уникурсальные графы. Теорема Эйлера
7.2 Алгоритм Флёри построения Эйлерового цыкла.
7.3 Эйлеров Путь в графе.
Эйлеров цикл — эйлеров путь, являющийся циклом. То есть замкнутый путь, проходящий через каждое ребро графа ровно по одному разу.