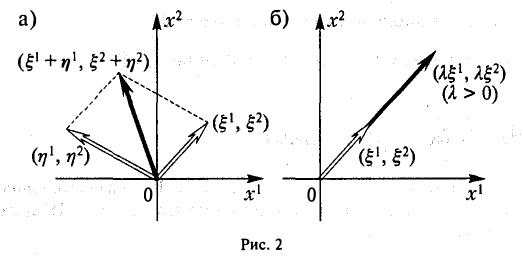
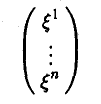
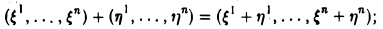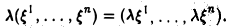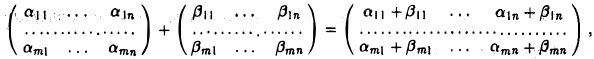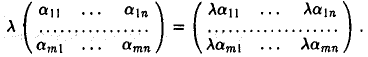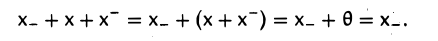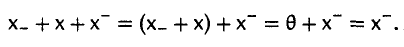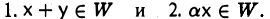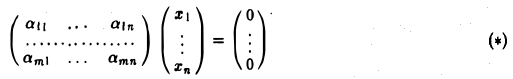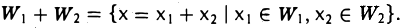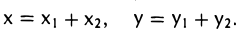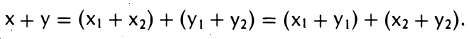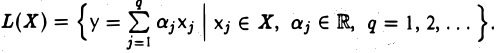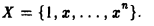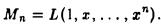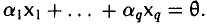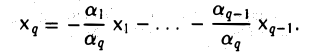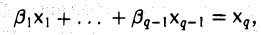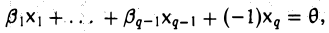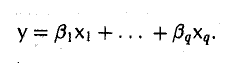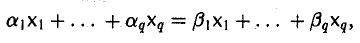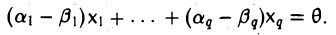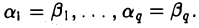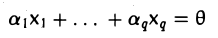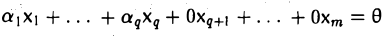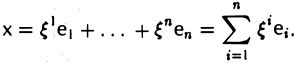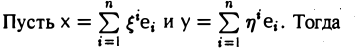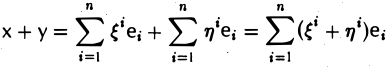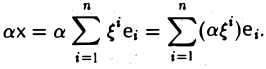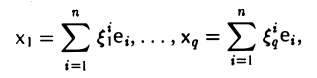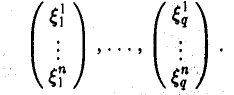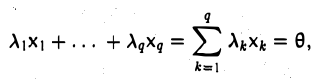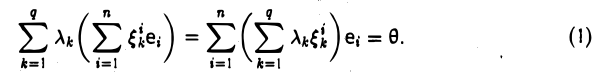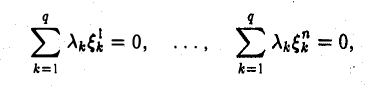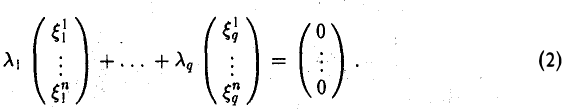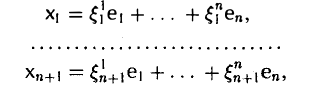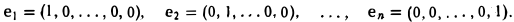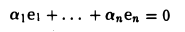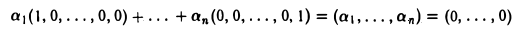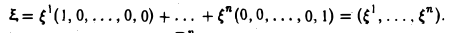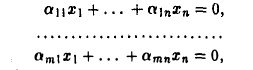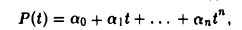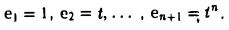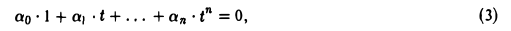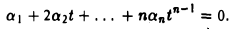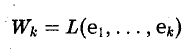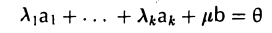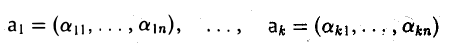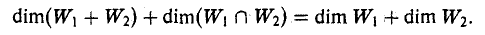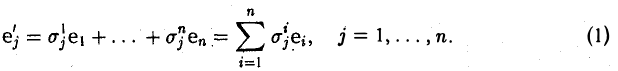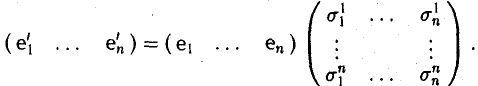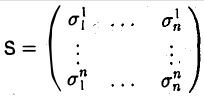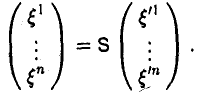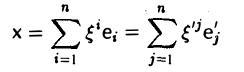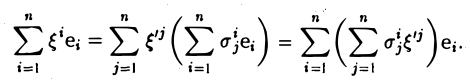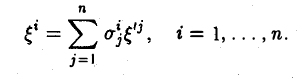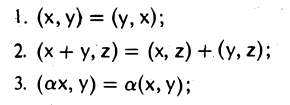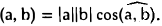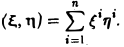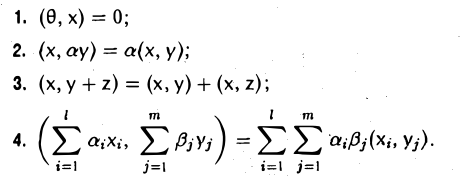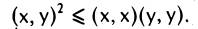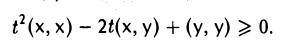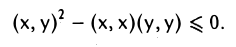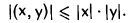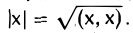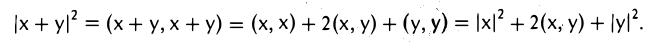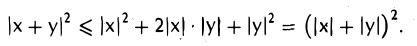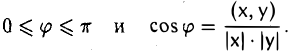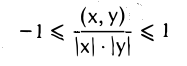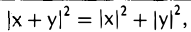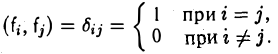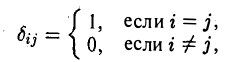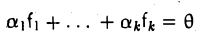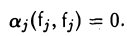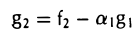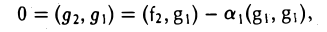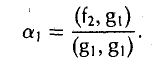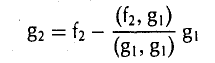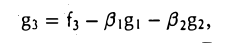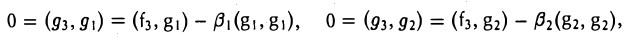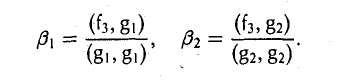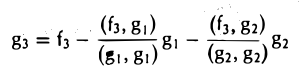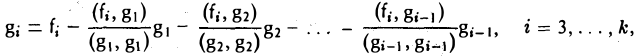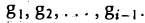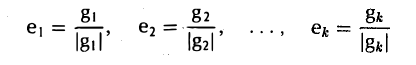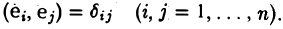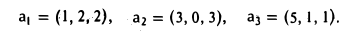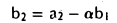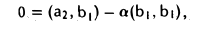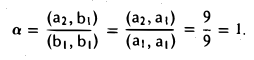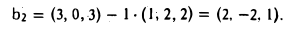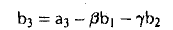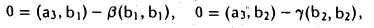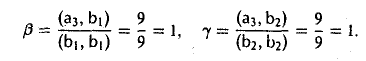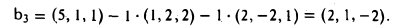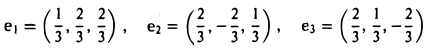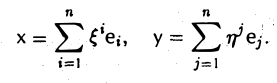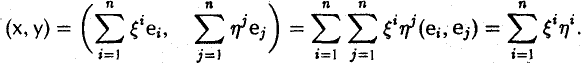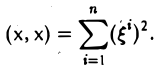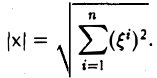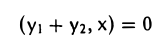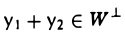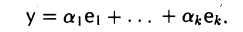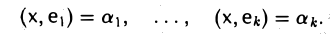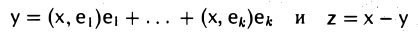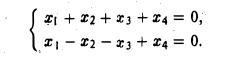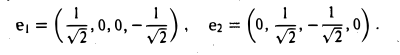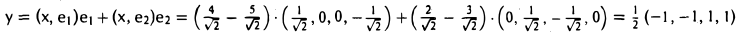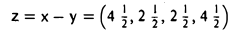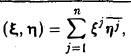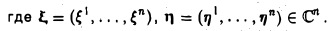Доказать что в пространстве функция является линейной формой

Линейные пространства: определение и примеры

Аксиомы линейного пространства

1. Аксиомы 1-4 показывают, что линейное пространство является коммутативной группой относительно операции сложения.

2. Аксиомы 5 и 6 определяют дистрибутивность операции умножения вектора на число по отношению к операции сложения векторов (аксиома 5) или к операции сложения чисел (аксиома 6). Аксиома 7, иногда называемая законом ассоциативности умножения на число, выражает связь двух разных операций: умножения вектора на число и умножения чисел. Свойство, определяемое аксиомой 8, называется унитарностью операции умножения вектора на число.

3. Линейное пространство — это непустое множество, так как обязательно содержит нулевой вектор.

4. Операции сложения векторов и умножения вектора на число называются линейными операциями над векторами.

Следствия аксиом линейного пространства

1. В линейном пространстве существует единственный нулевой вектор.

6. В выражениях вида (сумма конечного числа векторов) или (произведение вектора на конечное число множителей) можно расставлять скобки в любом порядке, либо вообще не указывать.

Остальные свойства доказываются аналогично.

Примеры линейных пространств

2. Обозначим — множества векторов (направленных отрезков) на прямой, на плоскости, в пространстве соответственно с обычными операциями сложения векторов и умножения векторов на число. Выполнение аксиом 1-8 линейного пространства следует из курса элементарной геометрии. Следовательно, множества являются вещественными линейными пространствами. Вместо свободных векторов можно рассмотреть соответствующие множества радиус-векторов. Например, множество векторов на плоскости, имеющих общее начало, т.е. отложенных от одной фиксированной точки плоскости, является вещественным линейным пространством. Множество радиус-векторов единичной длины не образует линейное пространство, так как для любого из этих векторов сумма не принадлежит рассматриваемому множеству.

5. Обозначим — множество матриц размеров с операциями сложения матриц и умножения матриц на число. Аксиомы 1-8 линейного пространства для этого множества выполняются. Нулевым вектором является нулевая матрица соответствующих размеров. Следовательно, множество является линейным пространством.

Множество многочленов степени не является линейным пространством, так как сумма таких многочленов может оказаться многочленом меньшей степени, не принадлежащим рассматриваемому множеству. Множество всех многочленов степени не выше, чем л, с положительными коэффициентами также не является линейным пространством, поскольку при умножении такого многочлена на отрицательное число получим многочлен, не принадлежащий этому множеству.

Все аксиомы выполняются. Следовательно, рассматриваемое множество является вещественным линейным пространством.

Линейные операции над линейными функциями задаются также, как в пункте 8 примеров линейных пространств. Сумма и произведение определяются равенствами:

Источник

Линейные отображения: определение, примеры, свойства

Определение линейных отображений

Напомним основные определения, связанные с понятием отображения (функции, оператора).

— инъективным, если разным элементам множества соответствуют разные образы: ;

— сюръективным, если для каждого элемента из множества имеется хотя бы один прообраз: ;

— биективным (взаимно однозначным), если оно инъективно и сюръективно одновременно.

Пусть и — линейные пространства (над одним и тем же числовым полем). Отображение называется линейным, если

2. и любого числа (из данного числового поля).

2. Условия аддитивности и однородности можно заменить одним условием линейности отображения:

и любых чисел и из данного числового поля.

3. При линейном отображении образ линейной комбинации является линейной комбинацией образов:

4. Взаимно однозначное линейное отображение является изоморфизмом.

Примеры линейных отображений

Свойства линейных отображений

Пусть — линейное отображение.

1. Если векторы линейно зависимы, то их образы также линейно зависимы.

4. Композиция линейных отображений является линейным отображением.

Однородность отображения доказывается аналогично.

5. Если линейное отображение обратимое (взаимно однозначное), то обратное отображение — линейное.

Докажем, например, аддитивность обратного отображения

6. Линейное отображение конечномерного пространства однозначно задается образами базисных векторов.

Линейные операции над линейными отображениями

Источник

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Благодарю Ю.А.Смолькина за обнаружение 07.08.19 ошибки на настоящей странице и информирование о ней.

Линейное пространство

Определения

Примеры линейных пространств

Почему множество решений системы неоднородных уравнений не образует линейного подпространства?

В пространстве квадратных матриц фиксированного порядка каждое из следующих подмножеств составляет линейное подпространство: симметричных, кососимметричных, верхнетреугольных, нижнетреугольных и диагональных матриц.

Изоморфизм

Линейная зависимость, базис, координаты

Пример. Для полиномов нескольких переменных свойство линейной зависимости является частным проявлением более общего свойства функциональной зависимости. Так, однородные полиномы (формы)

Теорема 2. а) Если система содержит хотя бы один нулевой вектор, то она л.з.

б) Если система л.н.з., то и любая ее подсистема л.н.з.

Две системы векторов называются эквивалентными если каждый вектор одной системы линейно выражается через векторы другой и обратно.

Теорема 4. Системы векторов

Теорема 5. Если каждая из двух эквивалентных систем

Пример [1]. Замечательный пример трехмерного линейного пространства дает нам совокупность всех цветов. Под суммой двух цветов будем понимать цвет, образованный их смешением

Анимация ☞ ЗДЕСЬ (1500 K, gif)

Пример. Найти базис подпространства

Ответ. Базис составляют, например, первая, вторая и четвертая строки.

Найти координаты полинома

Критерии линейной зависимости

Относительный базис

Сумма и пересечение линейных подпространств

Понятие пересечения линейных подпространств совпадает с понятием пересечения их как множеств.

Теорема. Имеет место формула:

Доказательство ☞ ЗДЕСЬ.

Можно ли обобщить этот результат на случай трех (и более подпространств)? Cправедлив ли, к примеру, аналог формулы включений-исключений в следующем виде:

Теорема. Имеет место формула:

Пример. Найти базис суммы и размерность пересечения

Найти базисы суммы и пересечения подпространств

Решение ☞ ЗДЕСЬ.

Прямая сумма линейных подпространств

Пример [2]. Доказать, что сумма подпространств

Линейные многообразия

Некоторые задачи на линейные многообразия ☞ ЗДЕСЬ.

Источник

Линейные и евклидовы пространства с примерами решения и образцами выполнения

Евклидово пространство — это вещественное линейное пространство, в котором зафиксирована симметричная положительно определенная билинейная форма. Значение билинейной формы на паре элементов называется скалярным произведением этих векторов.

Линейные и евклидовы пространства

Определение линейного пространства

Определение:

Множество V элементов х, у, z,… называется линейным пространством (действительным или комплексным), если по некоторому правилу

I. любым двум элементам х и у из V поставлен в соответствие элемент из V, обозначаемый х + у и называемый суммой элементов х и у;

II. любому элементу х из V и каждому числу а (вещественному или комплексному) поставлен в соответствие элемент из V, обозначаемый ах и называемый произведением элемента х на число а, и эти правила сложения и умножения на число удовлетворяют следующим аксиомам:

Элемент θ называется нулевым элементом, а элемент (-х) — противоположным элементу х.
Элементы х, у, z,… линейного пространства часто называют векторами. Поэтому линейное пространство называют также векторным пространством.

Примеры линейных пространств

Этим же свойством обладают: совокупность V1 векторов на прямой и совокупность V2 векторов на плоскости.

2, Совокупность упорядоченных наборов () из n действительных чисел.

Операции — сложение и умножение на действительное число — вводятся так:

б) умножение на число —

3. Совокупность всевозможных матриц Rmxn размера m х n с введенными правилами сложения матриц,

и умножения матрицы на число,

В частности, совокупность n-строк, R1xn и совокупность столбцов высоты m, Rmx1, являются линейными пространствами.

4. Множество С(-1, 1) вещественных функций, непрерывных на интервале (-1, I), с естественными операциями сложения функций и умножения функции на число.

Во всех приведенных примерах требования 1-8 проверяются непосредственно.

Простейшие свойства линейных пространств

2. Для любого элемента х противоположный ему элемент (—х) определен однозначно.

Пусть x — и х_ — элементы, противоположные элементу х. Покажем, что они равны.

Аналогично убеждаемся в том, что

Нетрудно убедится также в справедливости следующих свойств:

Линейные подпространства

Непустое подмножество W линейного пространства V называется линейным подпространством пространства V, если для любых элементов х и у из W и любого числа а выполняются следующие условия:

Иногда говорят: «множество W замкнуто относительно указанных операций».

Примеры линейных подпространств

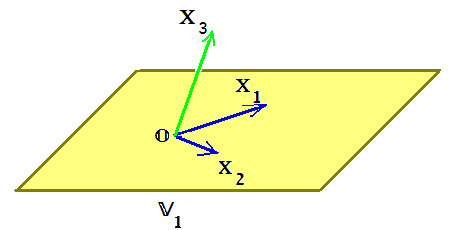
1.Множество векторов на плоскости V2 является линейным подпространством линейного пространства V3.

2. Совокупность решений однородной системы m линейных уравнений с n неизвестными

образует линейное подпространство линейного пространства Rnx1. В самом деле, сумма решений однородной системы () является решением этой же системы и произведение решения системы (*) на число также является ее решением.

3. Совокупность всех вещественнозначных функций, непрерывных на интервале (-1, 1) и обращающихся в нуль при t = 0, образует линейное подпространство линейного пространства С(— 1,1).

Сумма f(t) + g(t) функций f(t) и g(t), обращающихся в нуль при t = 0, t(0) = f(0) = 0, и произведение af(t) функции f(t), обращающейся в нуль при t = 0, f(0) = 0, на число а равны нулю при t = 0.

Свойства линейного подпространства

Сумма и пересечение линейных подпространств

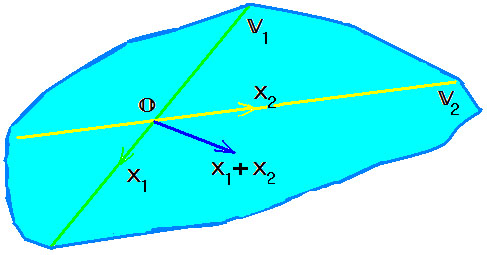
Пусть V — линейное пространство, W1 w W2 — его линейные подпространства. Суммой W1 + W2 линейных подпространств W1 и W2 называется совокупность всевозможных элементов х пространства V, которые можно представить в следующем виде

где x1 лежит в W1, а х2 — в W2. Коротко это можно записать так:

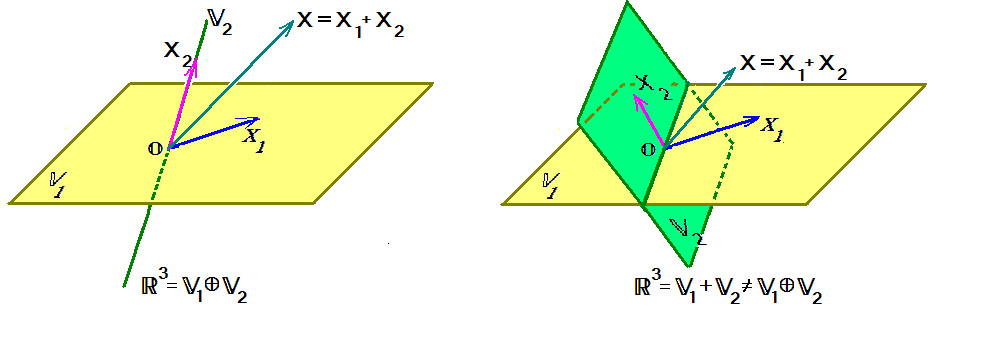
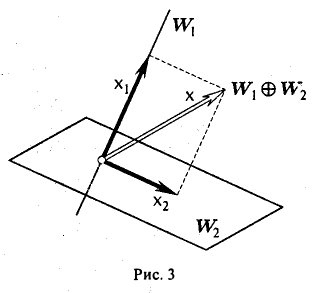
Сумма линейных подпространств W1 и W2 нaзывается прямой, если для каждого элемента х этой суммы разложение (1) единственно (рис. 3).

Обозначение: W1⊕W2

Пересечением W1 ∩ W2 линейных подпространств W1 и W2 линейного пространства V называется совокупность элементов, которые принадлежат одновременно и линейному подпространству W1, и линейному подпространству W2.

Свойства пересечения и суммы линейных подпространств

Возьмем в W1 + W2 два произвольных элемента х и у. По определению суммы подпространств найдутся элементы х1, у1, из W1 и х2, у2, из W2 такие, что

Это позволяет записать сумму х + у в следующем виде

Так как 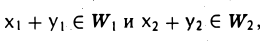то сумма х + у лежит в W1 + W2.

Аналогично доказывается включение ах ∈ W1 + W2.

2. Пересечение W1 ∩ W2 является линейным подпространством пространства V.

3. Если нулевой элемент является единственным общим вектором подпространств W1 й W2 линейного пространства V, то их сумма является прямой — W1 ⊕ W2.

Линейная оболочка

Линейной оболочкой L(X) подмножества X линейного пространства V называется совокупность всевозможных линейных комбинаций элементов из X,

Последнее читается так: «линейная оболочка L(X) состоит из всевозможных элементов у, представимых в виде линейных комбинаций элементов множества X».

Основные свойства линейной оболочки

Сумма линейных комбинаций элементов множества X и произведение линейной комбинации элементов на любое число снова являются линейными комбинациями элементов множества X.

3. L(X) — наименьшее линейное подпространство, содержащее множество X.

Пусть W — линейное подпространство, содержащее заданное множество X. Тогда произвольная линейная комбинация 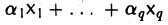элементов множества X — элемент линейной оболочки L(X) — содержится и в подпространстве W.

Пример:

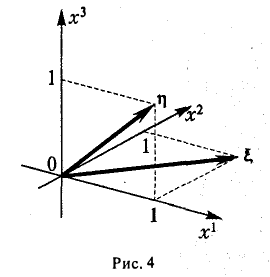
Рассмотрим в линейном пространстве R3 две тройки ξ = (1,1,0) и η = (1,0, I) (рис.4). Множество решений уравнения

Пример:

Рассмотрим в линейном пространстве С(- ∞, ∞) вещественнозначных функций, непрерывных на всей числовой оси, набор X одночленов 1, х,…, хn:

Линейная оболочка L(X) представляет собой совокупность многочленов с вещественными коэффициентами, степени которых не превосходят n.

Обозначение:

Линейная зависимость

Если равенство (1) выполняется только при а1 = … = аq = 0, то система элементов x1,…, хq называется линейно независимой.

Справедливы следующие утверждения.

Теорема:

Система элементов x1,…, хq (q ≥ 2) линейно зависима в том и только в том случае, если хотя бы один из ее элементов можно представить в виде линейной комбинации остальных.

Предположим сначала, что система элементов x1,…, xq линейно зависима. Будем Считать для определенности, что в равенстве (1) отличен от нуля коэффициент аq. Перенося все слагаемые, кроме последнего, в правую часть, после деления на аq ≠ 0 получим, что элемент хq является линейной комбинацией элементов х1 …, хq:

Обратно, если один из элементов равен линейной комбинации остальных,

то, перенося его в левую часть, получим линейную комбинацию

в которой есть отличные от нуля коэффициенты (-1 ≠ 0). Значит, система элементов x1,…., хq линейно зависима.

Теорема:

Из линейной независимости элементов x1…, xq вытекает, что a1 — β1 = … = аq — βq = 0 и, значит,

Теорема:

равны нулю не все коэффициенты.

Пример. Векторы из V2 линейно зависимы тогда и только тогда, когда они компланарны (рис.5).

Базис. Размерность

Упорядоченная система элементов e1,…, еn линейного пространства V называется базисом этого линейного пространства, если элементы e1,…, еn линейно независимы и каждый элемент из V можно представить в виде их линейной комбинации. Упорядоченность означает здесь, что каждому элементу приписан определенный (порядковый) номер. Из одной системы п элементов можно построить n! упорядоченных систем.

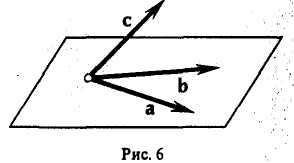
Пример:

Пусть a, b, с — тройка некомпланарных векторов из Vз (рис.6). Тогда упорядоченные тройки а, b, с; b, с, а; с, а, b; b, а, с; а, с, b и с, b, а — различные базисы V3.

Пусть с = (e1 … еn) — базис пространства V.

Тогда для любого элемента х из V найдется набор чисел такой, что

В силу теоремы 2 числа — координаты элемента х в базисе с — определены однозначно.

Посмотрим, что происходит с координатами элементов при простейших действиях с ними.

и для любого числа а

Таким образом, при сложении элементов их соответствующие координаты складываются, а при умножении элемента на число все его координаты умножаются на это число.

Координаты элемента часто удобно записывать в виде столбца. Например,

— координатный столбец элемента 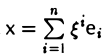в базисе e.

Разложим произвольную систему элементов x1,…, хq по базису e,

ли рассмотрим координатные столбцы элементов ч1,…, хq в этом базисе:

Теорема:

причем хотя бы один из коэффициентов λk отличен от нуля. Запишем это подробнее

Отсюда в силу единственности разложения элемента по базису вытекает, что

Таким образом, линейная комбинация координатных столбцов элементов x1,…, xq равна нулевому столбцу (с теми же коэффициентами λ1,…, λg). Это и означает, что система координатных столбцов линейно зависима.

Если же выполняется равенство (2), то, проводя рассуждения в обратном порядке, получаем формулу (1).

Тем самым, обращение в нуль некоторой нетривиальной (хотя бы один из коэффициентов отличен от нуля) линейной комбинации элементов линейного пространства равносильно тому, что нетривиальная линейная комбинация их координатных столбцов (с теми же коэффициентами) равна нулевому столбцу.

Теорема:

Пусть базис с линейного пространства V состоит из п элементов. Тогда всякая система из то элементов, где т > п, линейно зависима.

4 В силу теоремы 3 достаточно рассмотреть случай m = п + 1.

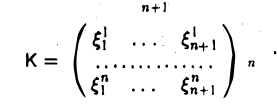
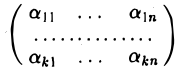
и запишем координаты элементов х1 …, xn+1 в виде матрицы, отводя j-й столбец координатам элемента xj, j = 1,…, п + 1. Получим матрицу из п строк и п + 1 столбцов —

Ввиду того, что ранг матрицы К не превосходит числа п ее строк, столбцы матрицы К (их п + 1) линейно зависимы. А так как это координатные столбцы элементов x1…..хп+1, то согласно теореме 4 система элементов x1…..хп+1 также линейно зависима.

Следствие:

Все базисы линейного пространства V состоят из одинакового числа элементов.
Пусть базис e состоит из п элементов, а базис e’ из п‘ элементов. В силу только что доказанной теоремы из линейной независимости системы е’1,…, е’n заключаем, что п’ ≤ п. Меняя базисы e и e’ местами, в силу этой же теоремы получаем, что п ≤ п’.

Тем самым, п = п’.
Размерностью линейного пространства V называется число элементов базиса этого пространства.

Пример:

Базис координатного пространства R» образуют элементы

Система элементов e1,e2, …,еп линейно независима: из равенства

и значит, a1 = … = an = 0.

Кроме того, любой элемент 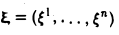из R» можно записать в виде линейной комбинации элементов e1…..еп: ‘

Тем самым, размерность пространства R» равна п.

Пример:

Однородная линейная система

имеющая ненулевые решения, обладает фундаментальной системой решений (ФСР). ФСР является базисом линейного пространства решений однородной системы. Размерность этого линейного пространства равна числу элементов ФСР, т.е. п — r, где r — ранг матрицы коэффициентов однородной системы, an — число неизвестных.

Пример:

Размерность линейного пространства Мп многочленов степени не выше п равна п + I.

Так как всякий многочлен P(t) степени не выше п имеет вид

то достаточно показать линейную независимость элементов

где t произвольно. Полагая t = 0, получаем, что ао = 0.

Продифференцируем равенство (3) по t:

Вновь положив t = 0, получим, что a1 = 0.

Линейное пространство, размерность которого равна п, называется п-мерным.

Обозначение: dim V = п.

Соглашение. Далее в этой главе всюду считается, если не оговорено противное, что размерность линейного пространства V равна п.

Ясно, что если W — подпространство n-мерного линейного пространства V, то dim W ≤ п.

Покажем, что в п-мерном линейном пространстве V есть линейные подпространства любой размерности k ≤ п.

Пусть e = (е1 … еn) — базис пространства V. Легко убедиться в том, что линейная оболочка

имеет размерность k.

По определению dim < θ >= 0.

Теорема:

так как в нетривиальной линейной комбинации

коэффициент μ ≠ 0 вследствие линейной независимости системы а1…., аk.

Если бы разложение вида (4) можно было бы написать для любого элемента b пространства V, то исходная система a1…, аk была бы базисом согласно определению. Но в силу условия k

строками которой являются координаты векторов а1, а2, а3, а4, равен четырем. Это означает, что строки матрицы А, а, значит, и векторы а1, а2, а3, а4 линейно независимы.

Подобный подход используется и в общем случае: чтобы дополнить систему k линейно независимых элементов

элементарными преобразованиями строк приводится к трапециевидной форме, а затем дополняется п — k строками вида

(0 … 1 … 0)

так, чтобы ранг получаемой матрицы был равен п. Справедливо следующее утверждение.

Теорема:

Пусть W1 и W2 — линейные подпространства линейного пространства V. Тогда

Замена базиса

Пусть e = (e1 … еn) и e’ = (е’1, … е’n) — базисы линейного пространства V. Разложим элементы базиса e’ по базису с. Имеем

Эти соотношения удобно записать в матричной форме
(2)

называется матрицей перехода от базиса e к базису e’.

Свойства матрицы перехода

Доказательство этого свойства проводится от противного.

Из равенства detS = 0 вытекает линейная зависимость столбцов матрицы S. Эти столбцы являются координатными столбцами элементов е’1,…, е’n в базисе e. Поэтому (и вследствие теоремы 4) элементы е’1…..с’n должны быть линейно зависимыми.

Последнее противоречит тому, что e’ — базис. Значит, допущение, что det S = 0, неверно.

2. Если и 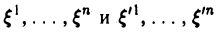— координаты элемента х в базисах e и e’ соответственно, то:
(3)

e’j их выражениями (1), получаем, что

Отсюда в силу единственности разложения элемента по базису имеем

Переходя к матричной записи найденных равенств, убеждаемся в справедливости свойства 2.

3. S -1 — матрица перехода от базиса e’ к базису e.

Свойство 3 доказывается умножением обеих частей матричного равенства (2) на матрицу S -1 справа.

Евклидовы пространства

Вещественное линейное пространство V называется (вещественным) евклидовым пространством, если любым двум элементам х и у из V ставится в соответствие число, обозначаемое через (х,у), такое, что для любых элементов х, y,z и произвольного вещественного числа а выполняются следующие условия:

4. (х, х) ≥ 0; причем равенство нулю возможно в том и только в том случае, если х = θ.

Число (х, у) называется скалярным произведением элементов х и у. Примеры евклидовых пространств.

2. Скалярное произведение произвольных элементов 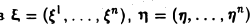из координатного пространства R» можно определить формулой

3, Линейное подпространство евклидова пространства само является евклидовым пространством.

Пользуясь определением евклидова пространства, нетрудно доказать следующие свойства:

Теорема:

Неравенство Коши—Буняковского. Для любых двух элементов х и у евклидова пространства V справедливо неравенство

Обратимся к случаю (х, х) ≠ 0. Тогда (х, х) > 0. По определению скалярного произведения неравенство

справедливо для любых элементов х и у из пространства V и любого вещественного числа t. Запишем неравенство (1) подробнее:

Левую часть последнего неравенства можно рассматривать как квадратный трехчлен относительно t. Из того, что знак этого квадратного трехчлена не изменяется при любых t, заключаем, что его дискриминант неположителен,

Перенося вычитаемое в правую часть, получаем требуемое неравенство.

Замечание:

Часто доказанное неравенство записывают в равносильной форме,

Следует подчеркнуть, что слева в этом неравенстве стоит абсолютная величина (модуль) скалярного произведения, а в правой части — нормы векторов х и у.

Определение:

Длиной (нормой) элемента х называется число |х|, вычисляемое по правилу

Ясно, что |х| ≥ 0 для любого х, причем равенство |х| = 0 возможно лишь в случае, если х = θ.

Рассмотрим цепочку равенств:

Заменяя второе слагаемое на 2|(х, у)| ≥ 2(х, у) и применяя неравенство Коши—Буняковского |(х,у)| ≤ |х| • |у|, получаем, что

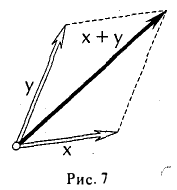
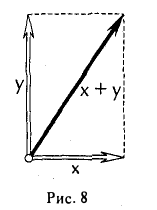
После извлечения квадратного корня приходим к неравенству треугольника:
|х + у| ≤ |х| + |у|
(рис.7).

Углом между ненулевыми элементами х и у евклидова пространства называется число φ, подчиненное следующим двум условиям:

Определение угла корректно, так как согласно теореме 8 имеем

для любых ненулевых элементов х и у.

Элементы х и у называются ортогональными, если (х, у) = 0. Для ортогональных элементов из соотношения (2) вытекает равенство

являющееся обобщением известной теоремы Пифагора’, квадрат длины суммы ортогональных элементов равен сумме квадратов их длин (рис. 8).

Система элементов f1…..f k называется ортогональной, если (fi, fj) =0′ при i ≠ j, и ортонормированной, если

Определение:

называют символом Кронекера.

Теорема:

Ортонормированная система элементов линейно независима.

Умножая обе части равенства

И так как (fj, fj) = 1,то aj = 0, j = 1,…, k.

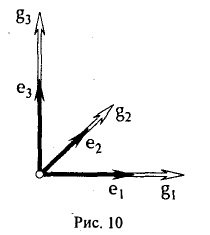
Метод ортогонализации

Для того, чтобы элемент

был ортогонален элементу g1, необходимо выполнение следующего равенства:

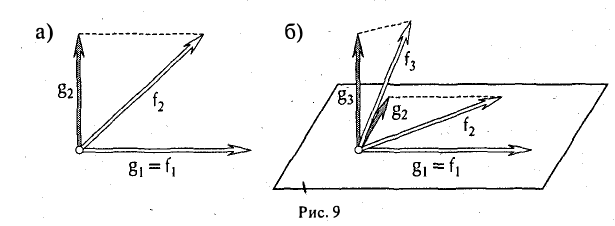
ортогонален элементу g1 (рис. 9 а).

Пользуясь построенными элементами g1, g2 и заданным элементом fз, построим элемент

ортогональный как элементу g1, так и элементу g2. Для этого коэффициенты β1 и β2 должны удовлетворять следующим условиям:

Таким образом, элемент
, (f3,g|) (f3,g2)

ортогонален элементам g1 и g2 (рис. 9 6).

Аналогичными рассуждениями можно показать, что элемент

ортогонален элементам

Делением каждого элемента gi (i = 1…..k) на его длину |g

Базис e = (e1 … еn) евклидова пространства называется ортонормированным, или ортобазисом, если

Суммируя вышеизложенное, получаем следующий результат.

Теорема:

В любом евклидовом пространстве существует о ртонормированный базис.
Пример:

Методом ортогонализации построить ортоиормированный базис евклидова пространства Е по его базису

Полагаем b1 = a1 и b2 = а2 — ab1. Для того, чтобы вектор

был ортогонален вектору b1, необходимо выполнение неравенства

Для того, чтобы вектор

был ортогонален векторам b1 и b2, необходимо выполнение равенств

Система векторов b1, b2, b3 ортогональна. Поделив каждый вектор на его длину, получим

— ортонормированный базис пространства Е.

При помощи ортонормированного базиса скалярное произведение элементов вычисляется особенно просто. Пусть e = (e1 … еn) — ортонормированный базис пространства Е. Вычислим скалярное произведение элементов х и у, предварительно разложив их по базису e

Ортогональное дополнение

Пусть W — линейное подпространство евклидова пространства V. Совокупность W⊥ элементов у пространства V, обладающих свойством

(y. х) = 0,

где х — произвольный элемент из W, называется ортогональным дополнением подпространства W. Другими словами, ортогональное дополнение W⊥ состоит из всех элементов у, ортогональных всем элементам подпространства W.

Свойства ортогонального дополнения

для любого элемента х из W. Складывая эти равенства и пользуясь свойствами скалярного произведения, получаем,что

для любого элемента х из W. Это означает, что

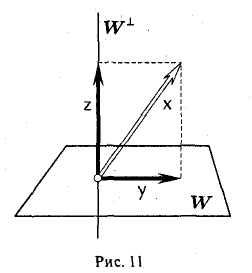
Свойство 2 означает, что любой элемент х пространства V можно представить, причем единственным образом, в виде суммы элементов из W и W⊥ :

x = y+z. ‘ (*)

Элемент у ∈ W называется ортогональной проекцией элемента х на линейное подпространство W, а элемент z ∈ W⊥ — его ортогональной составляющей (рис. 11).

Покажем, как по заданным элементу х и линейному подпространству W найти его ортогональную проекцию у и ортогональную составляющую г.

Можно считать, что в линейном подпространстве W задан ортонормированный базис e1…..еk. Запишем искомый элемент у в виде линейной комбинации

Подставляя это выражение в формулу (*):

и умножая обе части полученного равенства последовательно на элементы e1,…, еk, в предположении z ⊥ W приходим к соотношениям

обладают требуемыми свойствами. *

Пример:

Найти ортогональную проекцию вектора х = (4, 2, 3, 5) на линейное подпространство W ⊂ R4, заданное системой уравнений

Векторы a1 = (1,0,0,-1) и а2 = (0,1,-1,0) образуют фундаментальную систему решений и, следовательно, базис подпространства W. Кроме того, векторы a1 и а2 ортогональны. Для того, чтобы построить ортонормированный базис подпространства W, достаточно разделить эти векторы на иx длины. В результате получим

является ортогональной проекцией вектора х = (4,2, 3, 5), на подпространство W, а вектор

— его ортогональной составляющей.

Унитарные пространства

Унитарным пространством называется линейное комплексное пространство U, в котором каждой упорядоченной паре элементов х и у из U ставится в соответствие число — скалярное произведение (х, у) так, что для любых элементов х, у и z из U и любого комплексного числа а выполняются следующие соотношения:

Пример:

В координатном пространстве Сn, элементами которого являются всевозможные упорядоченные наборы п комплексных чисел, скалярное произведение можно ввести так

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник