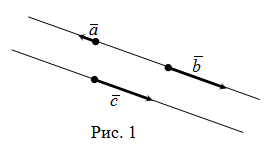
Доказать что векторы линейно зависимы

Линейная зависимость и независимость, свойства, исследование системы векторов на линейную зависимость, примеры и решения.

Понятия линейной зависимости и независимости системы векторов является очень важными при изучении алгебры векторов, так как на них базируются понятия размерности и базиса пространства. В этой статье мы дадим определения, рассмотрим свойства линейной зависимости и независимости, получим алгоритм исследования системы векторов на линейную зависимость и подробно разберем решения примеров.

Навигация по странице.

Определение линейной зависимости и линейной независимости системы векторов.

Так мы подошли к определению линейной зависимости системы векторов .

Если линейная комбинация может представлять собой нулевой вектор тогда, когда среди чисел есть хотя бы одно, отличное от нуля, то система векторов называется линейно зависимой.

Если линейная комбинация представляет собой нулевой вектор только тогда, когда все числа равны нулю, то система векторов называется линейно независимой.

Свойства линейной зависимости и независимости.

На основании данных определений, сформулируем и докажем свойства линейной зависимости и линейной независимости системы векторов.

Если к линейно зависимой системе векторов добавить несколько векторов, то полученная система будет линейно зависимой.

Так как система векторов линейно зависима, то равенство возможно при наличии хотя бы одного ненулевого числа из чисел . Пусть .

Добавим к исходной системе векторов еще s векторов , при этом получим систему . Так как и , то линейная комбинация векторов этой системы вида

представляет собой нулевой вектор, а . Следовательно, полученная система векторов является линейно зависимой.

Если из линейно независимой системы векторов исключить несколько векторов, то полученная система будет линейно независимой.

Предположим, что полученная система линейно зависима. Добавив к этой системе векторов все отброшенные векторы, мы получим исходную систему векторов. По условию – она линейно независима, а в силу предыдущего свойства линейной зависимости она должна быть линейно зависимой. Мы пришли к противоречию, следовательно, наше предположение неверно.

Если в системе векторов есть хотя бы один нулевой вектор, то такая система линейно зависимая.

Пусть вектор в этой системе векторов является нулевым. Предположим, что исходная система векторов линейно независима. Тогда векторное равенство возможно только тогда, когда . Однако, если взять любое , отличное от нуля, то равенство все равно будет справедливо, так как . Следовательно, наше предположение неверно, и исходная система векторов линейно зависима.

Если система векторов линейно зависима, то хотя бы один из ее векторов линейно выражается через остальные. Если система векторов линейно независима, то ни один из векторов не выражается через остальные.

Сначала докажем первое утверждение.

Пусть система векторов линейно зависима, тогда существует хотя бы одно отличное от нуля число и при этом верно равенство . Это равенство можно разрешить относительно , так как , при этом имеем

Следовательно, вектор линейно выражается через остальные векторы системы , что и требовалось доказать.

Теперь докажем второе утверждение.

Так как система векторов линейно независима, то равенство возможно лишь при .

Предположим, что какой-нибудь вектор системы выражается линейно через остальные. Пусть этим вектором является , тогда . Это равенство можно переписать как , в его левой части находится линейная комбинация векторов системы, причем коэффициент перед вектором отличен от нуля, что указывает на линейную зависимость исходной системы векторов. Так мы пришли к противоречию, значит, свойство доказано.

Из двух последних свойств следует важное утверждение:
если система векторов содержит векторы и , где – произвольное число, то она линейно зависима.

Исследование системы векторов на линейную зависимость.

Поставим задачу: нам требуется установить линейную зависимость или линейную независимость системы векторов .

Логичный вопрос: «как ее решать?»

Кое-что полезное с практической точки зрения можно вынести из рассмотренных выше определений и свойств линейной зависимости и независимости системы векторов. Эти определения и свойства позволяют нам установить линейную зависимость системы векторов в следующих случаях:

Как же быть в остальных случаях, которых большинство?

Напомним формулировку теоремы о ранге матрицы, которую мы приводили в статье ранг матрицы: определение, методы нахождения.

А теперь поясним связь теоремы о ранге матрицы с исследованием системы векторов на линейную зависимость.

Что будет означать линейная независимость системы векторов ?

Что же будет означать линейная зависимость системы векторов ?

Все очень просто: хотя бы одна строка матрицы A будет линейно выражаться через остальные, следовательно, линейная зависимость системы векторов будет равносильна условию Rank(A)

Итак, задача исследования системы векторов на линейную зависимость сводится к задаче нахождения ранга матрицы, составленной из векторов этой системы.

Следует заметить, что при p>n система векторов будет линейно зависимой.

Замечание: при составлении матрицы А векторы системы можно брать не в качестве строк, а в качестве столбцов.

Алгоритм исследования системы векторов на линейную зависимость.

Разберем алгоритм на примерах.

Примеры исследования системы векторов на линейную зависимость.

Дана система векторов . Исследуйте ее на линейную зависимость.

Так как вектор c нулевой, то исходная система векторов линейно зависима в силу третьего свойства.

система векторов линейно зависима.

Исследуйте систему векторов на линейную зависимость.

система векторов линейно зависима.

Является ли система векторов линейно зависимой?

Является ли система векторов линейно независимой?

Докажите, что система векторов

линейно независима.

Составим матрицу, строками которой будут векторы данной системы:

Покажем, что ранг этой матрицы равен количеству векторов исходной системы, то есть, четырем.

Переходим к поиску окаймляющего минора третьего порядка:

Осталось найти минор четвертого порядка, отличный от нуля. Вычислим определитель

Прибавим к первому столбцу третий, далее разложим определитель по элементам первого столбца:

Таким образом, ранг матрицы А равен четырем что доказывает линейную независимость исходной системы векторов.

Мы ознакомились с понятиями и свойствами линейной зависимости и линейной независимости системы векторов, получили метод исследования системы векторов на линейную зависимость, преобразовали его в алгоритм, и подробно разобрали решения характерных примеров.

Источник

Линейная зависимость системы векторов. Коллинеарные векторы

В данной статье мы расскажем:

Коллинеарные векторы

Коллинеарные векторы — это векторы, которые являются параллелями одной прямой или лежат на одной прямой.

Условия коллинеарности векторов

Два векторы являются коллинеарными, если выполняется любое из следующих условий:

Условие 2 неприменимо, если одна из координат вектора равна нулю.

Условие 3 применимо только к тем векторам, которые заданы в пространстве.

Примеры задач на исследование коллинеарности векторов

Исследуем векторы а = ( 1 ; 3 ) и b = ( 2 ; 1 ) на коллинеарность.

В данном случае необходимо воспользоваться 2-м условием коллинеарности. Для заданных векторов оно выглядит так:

Равенство неверное. Отсюда можно сделать вывод, что векторы a и b неколлинеарны.

Ответ: a | | b

Используя второе условие коллинераности, векторы будут коллинеарными, если их координаты будут пропорциональными:

Критерии линейной зависимости и линейной независимости систем векторов

Система векторов векторного пространства линейно зависима только в том случае, когда один из векторов системы можно выразить через остальные векторы данной системы.

в которой хотя бы один из коэффициентов комбинации не равен нулю.

Делим обе части равенства на ненулевой коэффициент:

Отсюда следует, что один из векторов системы выражается через все остальные векторы системы. Что и требовалось доказать (ч.т.д.).

Пусть один из векторов можно линейно выразить через все остальные векторы системы:

Переносим вектор e k в правую часть этого равенства:

Свойства линейно зависимых векторов

Примеры решения задач на линейную зависимость или линейную независимость векторов

Решение. Векторы являются линейно зависимыми, поскольку размерность векторов меньше количества векторов.

Решение. Находим значения коэффициентов, при которых линейная комбинация будет равняться нулевому вектору:

x 1 a + x 2 b + x 3 c 1 = 0

Записываем векторное уравнение в виде линейного:

Решаем эту систему при помощи метода Гаусса:

Из 2-ой строки вычитаем 1-ю, из 3-ей — 1-ю:

Из 1-й строки вычитаем 2-ю, к 3-ей прибавляем 2-ю:

Источник

04.07. Линейная зависимость векторов

Линейная зависимость векторов

Пусть даны три силы , , , лежащие в одной плоскости. Можно ли любую из них выразить через две другие? Эта задача очень часто встречается в физике. Если и не лежат на одной прямой (рис. 3.15, а), то сила может быть представлена через , и по правилу параллелограмма:

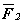
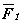
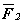
Рис. 3.15. Различные случаи расположения сил.

Если же и лежат на одной прямой, то эту задачу решить не удастся (рис. 3.15, б). Решение задачи окажется невозможным и в том случае, когда сила находится вне плоскости, которую образуют силы , , если они не лежат на одной прямой (рис. 3.15, в). Чтобы понять, почему это происходит, перейдем от геометрической иллюстрации этой задачи к ее строгому математическому анализу, основанному на понятии линейной зависимости векторов и исследовании свойств таких систем векторов.

Где – векторы, а – скаляры, называется ЛИНЕЙНОЙ КОМБИНАЦИЕЙ ВЕКТОРОВ. Его смысл состоит в том, что над системой векторов производятся линейные операции, введенные выше, в результате выполнения которых получается некоторый новый вектор, возможно даже нулевой, если, например, все множители . А если не все равны нулю, может ли их линейная комбинация обратиться в нуль? Оказывается, что условия, определяющие эту возможность, разделяют векторы на две принципиально различные группы.

Система векторов , среди которых есть ненулевые, называется ЛИНЕЙНО ЗАВИСИМОЙ, если их линейная комбинация обращается в нулевой вектор при условии, что Не все скалярные множители равны нулю, то есть

Система векторов называется ЛИНЕЙНО НЕЗАВИСИМОЙ, если их линейная комбинация обращается в нулевой вектор только при условии, что Все скалярные множители равны нулю, т. е.

Очевидно, если в системе векторов есть нулевой вектор, то она линейно зависима. Для доказательства этого факта достаточно в равенстве

Взять все коэффициенты равными нулю, за исключением одного – стоящего перед нулевым вектором (он может принимать любое отличное от нуля значение). Это и будет означать линейную зависимость данной системы векторов.

Если система из n векторов включает в себя m линейно зависимых, то она линейно зависима. Действительно, пусть первые m векторов линейно зависимы. Тогда в равенстве

Хотя бы один из скалярных коэффициентов отличен от нуля. Записав формально равенство

Где не все равны нулю, получим, что система векторов линейно зависима.

Рис. 3.16. Коллинеарные
Векторы.

Как геометрически представить себе линейно зависимые и линейно независимые векторы? Введем для этого два определения.

Векторы называются КОЛЛИНЕАРНЫМИ (рис. 3.16), если они лежат на параллельных прямых.

Нулевой вектор считается коллинеарным любому вектору.

Приведя эти векторы к общему началу, получим, что они располагаются на одной прямой.

Векторы, лежащие в параллельных плоскостях, называются КОМПЛАНАРНЫМИ (рис. 3.17). Нулевой вектор считается компланарным любой системе компланарных векторов.

Рис. 3.17. Компланарные векторы.

Если привести их к общему началу, то они окажутся расположенными в одной плоскости.

Из этих определений следует, что коллинеарность векторов можно рассматривать для системы, состоящей из двух или более векторов, а компланарность – для трех и более векторов.

Действительно, когда число векторов более одного, их приведение к одной прямой осуществимо не всегда. Для коллинеарных векторов этого удается добиться.

Термин «коллинеарность» характеризует взаимное расположение векторов, поэтому коллинеарность одного вектора лишена смысла.

Будут ли коллинеарные векторы компланарны? Будут ли компланарные векторы коллинеарны?

Аналогично, два вектора путем свободного переноса всегда можно расположить в одной плоскости. Поэтому они всегда компланарны. Этого может не быть, если число векторов больше двух. Если же векторы компланарны, то их всегда можно привести в одну плоскость.

Оказывается, коллинеарность и компланарность векторов неразрывно связаны с их линейной зависимостью. Мы докажем сейчас теоремы, которые соединяют эти понятия и служат предпосылками для введения центрального понятия всей математики – СИСТЕМЫ КООРДИНАТ.

ТЕОРЕМА 1. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Слова «тогда и только тогда», как известно, означают, что имеет место прямая и обратная теоремы. Сформулируем их и докажем.

Необходимость. Если два вектора линейно зависимы, то они коллинеарны.

ДОКАЗАТЕЛЬСТВО. Пусть векторы и линейно зависимы. Тогда в равенстве

Хотя бы один из скалярных множителей или отличен от нуля. Пусть для определенности . Тогда

Где , что означает коллинеарность векторов и .

Достаточность. Если два вектора коллинеарны, то они линейно зависимы.

ДОКАЗАТЕЛЬСТВО. Пусть векторы и коллинеарны. Тогда, очевидно, они связаны соотношением

Это означает, что линейная комбинация векторов и обращается в нулевой вектор, причем скалярный множитель при векторе не равен нулю, то есть система векторов и линейно зависима.

Наряду с доказанной теоремой, могут быть сформулированы еще две, являющиеся ее следствиями.

Сформулируйте эти утверждения с помощью предикатов.

Следствие 1. Если два вектора не являются линейно зависимыми, то они не будут коллинеарны.

Следствие 2. Если два вектора не являются коллинеарными, то они не будут линейно зависимы.

ТЕОРЕМА 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.

Необходимость. Если три вектора линейно зависимы, то они компланарны.

Рис. 3.18. Связь
между линейной
зависимостью
и компланарностью.

ДОКАЗАТЕЛЬСТВО. Пусть векторы , и линейно зависимы (рис. 3.18). Тогда в равенстве

Хотя бы один из скалярных множителей , или отличен от нуля. Пусть для определенности . Тогда

То есть вектор – диагональ параллелограмма, построенного на векторах и как на сторонах (по правилу сложения векторов). Но векторы и , а также И попарно коллинеарны. Следовательно, и лежат в плоскости этого же параллелограмма, то есть , и – компланарны.

В случае коллинеарности векторов и компланарность , и очевидна.

Достаточность. Если три вектора компланарны, то они линейно зависимы.

Рис. 3.19. Связь между компланарностью и линейной зависимостью векторов.

ДОКАЗАТЕЛЬСТВО. Пусть , и компланарны (рис. 3.19), то есть они лежат в одной плоскости и хотя бы два из них, например, и , неколлинеарны. После приведения системы векторов к общему началу вектор можно разложить по направлениям неколлинеарных векторов и , то есть представить его в виде суммы векторов, лежащих на прямых, задаваемых векторами и :

Но , , поэтому

или .

Поскольку имеется хотя бы один скалярный множитель, отличный от нуля, то , и линейно зависимы.

Могут ли быть среди трех некомпланарных векторов два коллинеарных?

Следствие 1. Если три вектора не являются линейно зависимыми, то они не будут компланарны.

Следствие 2. Если три вектора не являются компланарными, то они не будут линейно зависимы.

ТЕОРЕМА 3. Всякий вектор может быть единственным образом разложен по трем некомпланарным векторам.

Теорема означает, что если векторы , и некомпланарны и вектор произволен, то существует единственное представление

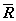
ДОКАЗАТЕЛЬСТВО. Приведем векторы , , и к общему началу (рис. 3.20). Пусть точка L – конец вектора , а точка М – определяет пересечение вспомогательной прямой LM, параллельной вектору , с плоскостью векторов и . Рассмотрим вспомогательные отрезки . Тогда, по правилу сложения векторов,

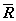
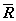
Рис. 3.20. Разложение вектора по трем
некомпланарным
направлениям.

Но векторы и , и , и коллинеарны, поэтому

. (3.1)

Покажем, что это разложение единственно. Предположим противное, что существует другое представление 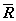через векторы , И :

(3.2)

И хотя бы один из коэффициентов не равен соответствующему коэффициенту . Пусть для определенности . Тогда, вычитая из (3.1) равенство (3.2), получим:

Полученное соотношение означает, что линейная комбинация векторов , и равна нулевому вектору, но скалярный коэффициент при векторе отличен от нуля, то есть векторы , и линейно зависимы, а потому компланарны, что противоречит условию теоремы. Следовательно, предположение о справедливости равенства (3.2) наряду с равенством (3.1), неверно, то есть разложение (3.1) единственно.

Следствие. Любые четыре вектора в пространстве линейно зависимы.

Действительно, если , и некомпланарны, то из равенства (3.1) следует:

Скалярный коэффициент при векторе 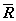не равен нулю. Следовательно, четыре вектора в пространстве линейно зависимы.

Если же какие-то три из векторов , , , компланарны, то они будут линейно зависимы, а значит приведут к линейной зависимости всю систему векторов.

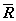
Если какие-то два из четырех векторов коллинеарны, то это означает их линейную зависимость и, следовательно, линейную зависимость всех четырех векторов.

Таким образом, любые четыре вектора в пространстве линейно зависимы.

Вернемся теперь к задачам, поставленным в начале параграфа. Если силы и лежат на одной прямой и силу необходимо выразить через эти векторы, то ясно, что подобная задача неразрешима, так как всякая линейная комбинация сил и есть некоторый вектор

Лежащий на этой прямой и неколлинеарный вектору .

Если две из трех сил коллинеарны, то их можно параллельным переносом привести в одну плоскость, а значит они линейно зависимы. В их линейной комбинации, приравненной к нулю, есть хотя бы один коэффициент, отличный от нуля, что позволяет выразить одну силу через две другие. Если же силы , и представляют собой неколлинеарные друг другу векторы, то, располагаясь в одной плоскости, они образуют линейно зависимую систему векторов, что обеспечивает возможность выразить одну из них через две другие.

Если векторы линейно зависимы, то всякий ли вектор можно выразить через остальные?

Когда одна из сил, например , лежит вне плоскости, образуемой силами и , то система векторов , , становится некомпланарна, а значит, линейно независимой, поэтому между ними возможно лишь соотношение:

0.

Источник