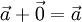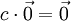Доказать что векторы нулевые

22. Простейшие свойства векторного пространства

Рассмотрим те свойства векторного пространства, которые вытекают из его определения.

Свойство 1. В векторном пространстве V существует единственный нулевой вектор 0.

Доказательство. Допустим противное, что в V имеется два нулевых вектора 0 И Тогда по аксиомам 3° и 1° имеем

0 = 0 + = + 0 = .

Свойство 2. В векторном пространстве для любого вектора существует единственный противоположный вектор —.

Доказательство. См. доказательство теоремы 7 из §1.

Свойство 6. Для любых векторов , если A + B = А + С, то B = С.

Свойство 7. Для любых векторов Если A + B = А, то B = 0.

Доказательство. Следует из свойства 6.

Свойство 8. Для любого вектора Имеем 0×A = 0.

Доказательство. По аксиомам 8° и 6° имеем

Отсюда по свойству 7 0×A = 0.

Свойство 9. Для любого числа Имеем a×0 = 0.

Доказательство. По аксиоме 5° имеем

Отсюда по свойству 7 a×0 = 0.

Свойство 10. Пусть , . a×А = 0 Тогда и только тогда, когда a=0 Или А = 0.

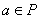
Противоречие. Свойство доказано.

Свойство 11. Пусть , . Тогда И

Доказательство. По аксиоме 6° и свойству 8 имеем

Отсюда в силу единственности противоположного вектора получаем требуемые равенства.

Свойство 12. Для любых , , Если

Доказательство. По определению разности, аксиоме 6 и свойству 11 имеем

Аналогичным образом доказываются следующие три свойства, которые рекомендуется доказать читателю самостоятельно.

Свойство 13. Для любых Имеем

Свойство 14. Для любых ,Если , То A = B.

Свойство 15. Для любых , Если , То

Источник

Нуль-вектор

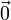
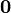
Нулевой вектор (нуль-вектор) — вектор, начало которого совпадает с его концом. Нулевой вектор имеет норму 0 и обозначается или .

С нулевым вектором не связывают никакого направления в пространстве (т.е. его можно считать направленным во все стороны). Нулевой вектор принято считать сонаправленным любому вектору. Считается, что нулевой вектор одновременно параллелен и перпендикулярен любому вектору пространства.

Все координаты нулевого вектора в любой аффинной системе координат равны нулю.

Для любого вектора

Для любого числа c

Нулевой вектор равен сумме любых двух противоположных векторов:

.

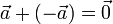
См. также

Ссылки

Полезное

Смотреть что такое «Нуль-вектор» в других словарях:

нуль-вектор — нуль вектор, нуль вектора … Орфографический словарь-справочник

нуль-вектор — nulinis vektorius statusas T sritis fizika atitikmenys: angl. null vector; zero vector vok. Nullvektor, m rus. нулевой вектор, m; нуль вектор, m pranc. vecteur nul, m; vecteur zéro, m … Fizikos terminų žodynas

нуль-вектор — (2 м), Р. нуль ве/ктора … Орфографический словарь русского языка

нуль-вектор — а, ч., мат. Вектор, що є тотожним перетворенням простору … Український тлумачний словник

Вектор (математика) — Вектор У этого термина существуют и другие значения, см. Вектор … Википедия

Нуль — Нуль: В Викисловаре есть статья «нуль» Нуль, 0 (число) целое число, разделяющее на числовой прямой положительные и отрицательные числа … Википедия

Вектор-функция — Вектор функция функция, значениями которой являются векторы в векторном пространстве двух, трёх или более измерений. Аргументами функции могут быть: одна скалярная переменная тогда значения вектор функции определяют в некоторую… … Википедия

ВЕКТОР — В физике и математике вектор это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент,… … Энциклопедия Кольера

Вектор Киллинга — Поле Киллинга векторное поле скоростей (локальной) однопараметрической группы движений риманова или псевдориманова многообразия. Другими словами, поток, который генерируется векторным полем Киллинга, задает непрерывное однопараметрическое… … Википедия

Источник

Линейная зависимость системы векторов. Коллинеарные векторы

В данной статье мы расскажем:

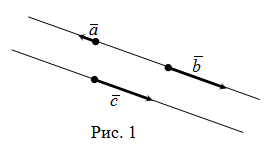
Коллинеарные векторы

Коллинеарные векторы — это векторы, которые являются параллелями одной прямой или лежат на одной прямой.

Условия коллинеарности векторов

Два векторы являются коллинеарными, если выполняется любое из следующих условий:

Условие 2 неприменимо, если одна из координат вектора равна нулю.

Условие 3 применимо только к тем векторам, которые заданы в пространстве.

Примеры задач на исследование коллинеарности векторов

Исследуем векторы а = ( 1 ; 3 ) и b = ( 2 ; 1 ) на коллинеарность.

В данном случае необходимо воспользоваться 2-м условием коллинеарности. Для заданных векторов оно выглядит так:

Равенство неверное. Отсюда можно сделать вывод, что векторы a и b неколлинеарны.

Ответ: a | | b

Используя второе условие коллинераности, векторы будут коллинеарными, если их координаты будут пропорциональными:

Критерии линейной зависимости и линейной независимости систем векторов

Система векторов векторного пространства линейно зависима только в том случае, когда один из векторов системы можно выразить через остальные векторы данной системы.

в которой хотя бы один из коэффициентов комбинации не равен нулю.

Делим обе части равенства на ненулевой коэффициент:

Отсюда следует, что один из векторов системы выражается через все остальные векторы системы. Что и требовалось доказать (ч.т.д.).

Пусть один из векторов можно линейно выразить через все остальные векторы системы:

Переносим вектор e k в правую часть этого равенства:

Свойства линейно зависимых векторов

Примеры решения задач на линейную зависимость или линейную независимость векторов

Решение. Векторы являются линейно зависимыми, поскольку размерность векторов меньше количества векторов.

Решение. Находим значения коэффициентов, при которых линейная комбинация будет равняться нулевому вектору:

x 1 a + x 2 b + x 3 c 1 = 0

Записываем векторное уравнение в виде линейного:

Решаем эту систему при помощи метода Гаусса:

Из 2-ой строки вычитаем 1-ю, из 3-ей — 1-ю:

Из 1-й строки вычитаем 2-ю, к 3-ей прибавляем 2-ю:

Источник

Геометрия

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Понятие вектора в пространстве

Напомним, что в курсе планиметрии мы уже подробно изучали вектора и действия с ними. При этом предполагалось, что все вектора располагаются в одной плоскости. Однако можно расширить понятие вектора так, чтобы они использовались и в стереометрии. В таком случае вектора уже могут располагаться в различных плоскостях.

Начнем с определения вектора:

Конец вектора обозначают с помощью стрелки. Посмотрим на рисунок:

Здесь показаны сразу три вектора:

У вектора АВ начало находится в точке А, а конец – в точке В. Аналогично у вектора С D точка С – это начало, а D – это конец. В обоих случаях начало и конец – это различные точки, поэтому АВ и CD именуют ненулевыми векторами. Если же начало и конец находятся в одной точке, например в Т, то получается нулевой вектор ТТ. Всякую точку в пространстве можно рассматривать как нулевой вектор:

Длина вектора АВ – это длина соответствующего ему отрезка АВ. Для обозначения длины используют квадратные скобки:

Естественно, что нулевой вектор имеет нулевую длину.

Далее напомним понятие коллинеарных векторов:

Коллинеарные вектора могут быть либо сонаправленными, либо противоположно направленными. Сонаправленные вектора находятся на сонаправленных лучах. Рассмотрим пример с кубом:

Здесь показаны вектора AD и ВС. Они сонаправленные, этот факт записывается так:

Вектора AD и FE располагаются на скрещивающихся прямых, поэтому они не коллинеарны. Их нельзя считать ни сонаправленными, ни противоположно направленными.

Сонаправленные вектора, имеющие одинаковую длину, именуются равными.

Рассмотрим несколько простейших задач.

Задание. В прямоугольном параллелепипеде АВС DA ₁ B ₁ C ₁ D ₁ известны три его измерения:

Решение. Для нахождения длин этих векторов достаточно вычислить длину отрезков СВ, DB и DB ₁. Проще всего вычислить СВ, ведь отрезки СВ и AD одинаковы как стороны прямоугольника АВ CD :

Вектора АМ и МВ также коллинеарны и имеют одинаковую длину, но они противоположно направлены, а потому равными не являются.

Операции над векторами

Такой метод сложения векторов именуется правилом треугольника. Если нужно сложить больше двух векторов, то используют правило многоугольника. В этом случае необходимо каждый следующий вектор откладывать от конца предыдущего. При этом в стереометрии вектора могут располагаться в различных плоскостях, то есть они на самом деле многоугольник не образуют:

Напомним, что в планиметрии существовали так называемые противоположные вектора. Есть они и в стереометрии:

Главное свойство противоположных векторов заключается в том, что в сумме они дают нулевой вектор:

Заметим, что для получения противоположного вектора достаточно поменять его начало и конец, то есть в записи вектора обозначающие его буквы надо просто записать в обратном порядке:

1) b и a будут коллинеарными векторами;

Если k – положительное число, то вектора a и b будут сонаправленными. Если же k a и b будут направлены противоположно.

Задание. Дан параллелепипед АВС D А₁В₁С₁ D ₁. Постройте вектор, который будет являться суммой векторов:

Решение. В каждом случае необходимо заменить один из векторов в сумме на другой равный ему вектор так, чтобы можно было применить правило треугольника.

В задании а) вектор А₁ D ₁ заменить равным ему вектором ВС. В итоге получится вектор АС.

В задании б) заменяем А D ₁ на вектор ВС₁. Также можно было бы заменить АВ на D ₁ C ₁. В обоих случаях сумма окажется равной АС₁.

В задании в) удобно DA заменить на C ₁В₁, тогда искомой суммой будет вектор С₁В.

В задании г) производим замену DD ₁ на равный ему вектор BB ₁. Тогда сумма DB и BB ₁– это вектор DB ₁.

В задании д) необходимо заменить ВС на В₁С₁. В итоге получаем вектор DC :

Решение. В случае а) сначала запишем очевидное равенство векторов, вытекающее из правило многоугольника:

Обратите внимание, что здесь у каждого следующего слагаемого начальная точка совпадает с конечной точкой предыдущего слагаемого, поэтому равенство и справедливо:

Однако по условию а) нам надо использовать другие вектора для выражения АВ. Мы можем просто заменить вектора CD и DB на противоположные:

Теперь можно составить и выражение для АВ:

Аналогично решаем и задания б) и в):

Задание. Р – вершина правильной шестиугольной пирамиды. Докажите, что сумма векторов, совпадающих с ребрами этой пирамиды и начинающихся в точке Р, в точности равна сумме векторов, которые совпадают с апофемами пирамиды и при этом также начинаются в точке Р.

Решение. Обозначим вершины буквами А₁, А₂, … А₆, а середины сторон шестиугольника, лежащего в основании, буквами Н₁, Н₂, … Н₆, как это показано на рисунке:

Нам надо показать, что сумма красных векторов равна сумме черных векторов:

Теперь отдельно построим правильный шестиугольник, лежащий, в основании пирамиды:

Ясно, что вектора, образованные сторонами этого шестиугольника, в сумме дают нулевой вектор (по правилу многоугольника):

Так как точки Н₁, Н₂, … Н₆ – середины сторона, то вектора Н₆А₆, Н₅А₅,…Н₁А₁ будут вдвое короче векторов А₁А₆, А₆А₅, … А₂А₁. При этом они находятся на одних прямых, поэтому справедливы равенства:

Таким образом нам удалось из верного равенства (3) доказать (2), из которого в свою очередь следует справедливость и (1), ч. т. д.

Задание. Упростите выражения:

Решение. Здесь надо просто применить законы сложения и умножения векторов, как это делалось и в курсе планиметрии. Сначала раскрываем скобки, а потом приводим подобные слагаемые:

Компланарные векторы

Если мы отложим несколько векторов от одной точки, то они либо будут находиться в одной плос-ти, либо располагаться в различных плос-тях. В первом случае их именуют компланарными векторами, а во втором – некомпланарными.

Любые два вектора будут компланарны, ведь при их откладывании от одной точки мы получаем две пересекающихся прямых, а через них всегда можно провести плос-ть. Однако если векторов более двух, то они могут быть как компланарны, так и некомпланарны.

Рассмотрим для примера параллелепипед:

Здесь вектора АС, АВ и АD компланарны, так как все они принадлежат одной грани (то есть плос-ти) АВСD. А вектора АВ, АD и АА₁ некомпланарны, ведь через них нельзя провести одну плос-ть.

Очевидно, что если из трех векторов любые два коллинеарны, то вся тройка векторов компланарна, ведь при откладывании векторов от одной точки коллинеарные вектора окажутся на одной прямой.

Существует признак компланарности векторов:

Напомним, что подразумевается под разложением вектора. Пусть есть вектора а, b и c. Если существуют такие числах и y, при которых выполняется равенство

то говорят, что вектор с разложен по векторам а и b, причем числа xи y называются коэффициентами разложения.

Докажем сформулированный признак. Пусть есть три вектора а, b и c, а также числа xи y, такие, что

Эти вектора находятся в одной плос-ти ОАВ. Теперь от той же точки О отложим вектора ха и уb, концы которых окажутся в точках А₁ и В₁:

Естественно, что вектора ОА₁ и ОВ₁ также окажутся в плос-ти ОАВ. Тогда и их сумма будет принадлежать этой плос-ти, а эта сумма как раз и есть вектор с:

В итоге получили, что а, b и с располагаются в одной плос-ти, то есть они компланарны.

Справедливо и обратное утверждение. Если вектора а, b и с компланарны, но а и b неколлинеарны, то вектор с можно разложить на вектора a и b. Это утверждение прямо следует из изученной в 9 классе теоремы о разложении векторов. Важно отметить, что коэффициенты такого разложения определяются однозначно.

Для сложения тройки некомпланарных векторов можно применить так называемое правило параллелепипеда. Если есть три некомпланарных вектора, то можно отложить их от одной точки О и далее построить параллелепипед, в котором эти вектора будут ребрами. Тогда диагональ этого параллелепипеда, выходящая из точки О, и будет суммой этих трех векторов:

Разложение вектора на некомпланарные вектора

Иногда вектор можно разложить не на два, а на три вектора. Выглядит такое разложение так:

Для доказательства рассмотрим три некомпланарных вектора а, bи c, а также произвольный вектор р. Отложим их от одной точки О. Обозначим концы этих векторов большими буквами А, В, С и Р:

Через ОВ и ОА можно провести некоторую плос-ть α. Точка С ей принадлежать не может, ведь ОА, ОВ и ОС – некомпланарные вектора. Проведем через Р прямую, параллельную ОС. Так как ОС пересекает α, то и параллельная ей прямая также пересечет α в некоторой точке Р₁. (Примечание. Если Р принадлежит α, то точки Р и Р₁ совпадут, то есть вектор Р₁Р будет нулевым).

Далее через точку Р₁ в плос-ти α проведем прямую, параллельную ОВ, которая пересечет ОА в точке Р₂. Заметим, что вектор ОР₂ находится на той же прямой, что и вектор ОА, то есть они коллинеарны, поэтому существует такое число х, что

Итак, мы показали, что у произвольного вектора p есть разложение на заранее заданные некомпланарные вектора. Осталось показать, что существует только одно такое разложение. Докажем это методом от противного. Пусть есть второе разложение с другими коэффициентами х₁, у₁ и z₁:

В правой части находятся три вектора, которые в сумме нулевой вектор. По правилу сложения векторов это означает, что эти вектора образуют треугольник, то есть находятся в одной плос-ти:

Значит, они компланарны. Тогда компланарны и вектора a, b и с, что противоречит условию теоремы. Значит, второго разложения р на заданные некомпланарные векторы не существует, ч. т. д.

Задание. АВСD и А₁В₁С₁D₁ – параллелограммы, располагающиеся в разных плос-тях. Докажите, что тройка векторов ВВ₁, СС₁ и DD₁ компланарна.

Решение. Сначала построим рисунок по условию задачи:

Для доказательства используем признак компланарности векторов. Для этого надо один из векторов, отмеченных на рисунке красным, разложить на два других вектора.

В результате нам удалось разложить СС₁ на вектора BB₁ и CC₁. Значит, эти три вектора коллинеарны.

Задание. В параллелепипеде АВСDA₁B₁C₁D₁ запишите разложение вектора BD₁ по векторам ВА, ВС и ВВ₁.

Решение. Сначала представим вектор BD₁ как сумму трех векторов:

Теперь заметим, что вектора С₁D₁ и ВА соответствуют ребрам параллелепипеда. Эти ребра одинаковы по длине и параллельны, поэтому и вектора будут равными. Аналогично равны вектора СС₁ и ВВ₁:

Задание. АВСD – тетраэдр, а точка К делит его ребро ВС пополам. Разложите вектор DK по векторам DA, AB и AC.

Решение. Сначала запишем очевидное выражение для вектора DK:

Задание. В точке М пересекаются медианы треугольника АВС, а О – произвольная точка в пространстве. Разложите вектор ОМ по векторам ОА, ОВ и ОС.

Решение. Медиану, проходящую через точку А, мы обозначим как АА₁, то есть А₁ – это середина отрезка ВС. Также буквой К обозначим середину ОВ:

Сначала разложим вектор ОА₁ на ОВ и ОС. Это можно сделать, ведь они компланарны. КА₁ – это средняя линия ∆ОСВ, поэтому КА₁||ОС и КА₁ вдвое короче ОС. Это значит, что

Так как АА₁ – медиана, то точка М делит ее в отношении 2:1. Отсюда вытекает следующее соотношение:

Только что решенная задача может быть использована и при решении другого, более сложного задания.

Задание. Докажите, что в параллелепипеде АВСDА₁В₁С₁D₁ плос-ти А₁ВD и СB₁D₁ делят диагональ АС₁ на три равных отрезка.

Решение. Обозначим точкой K точку пересечения медиан ∆А₁ВD. Тогда по формуле, выведенной в предыдущей задаче, мы получаем, что

Это соотношение означает, что вектора АК и АС₁ коллинеарны, поэтому они располагаются на одной прямой (они не могут находиться на параллельных прямых, ведь у них есть общая точка А). Значит, точка K принадлежит диагонали АС₁, и отрезок АК втрое короче диагонали.

Аналогично можно показать, что и

Из этого также вытекает, что М принадлежит диагонали АС₁, и МС₁ втрое короче АС₁. Значит, точки М и К делят диагональ на три равных отрезка, ч. т. д.

Сегодня мы расширили понятие векторов и научились их применять не только в планиметрических, но и в стереометрических задачах. При сохраняются все правила, по которым выполняются действия над векторами. Также в стереометрии появляется новое понятие компланарных и некомпланарых векторов.

Источник