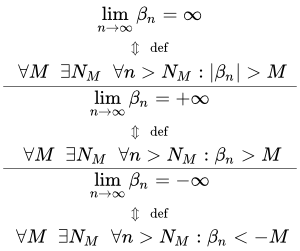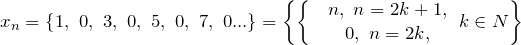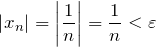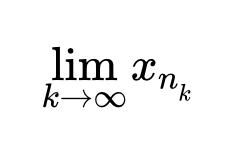Доказать что всякая неограниченная последовательность либо является бесконечно большой

Определение бесконечно большой последовательности

Определение

Последовательности с пределами (2) и (3) являются частными случаями бесконечно большой последовательности (1). Из этих определений следует, что если предел последовательности равен плюс или минус бесконечности, то он также равен и бесконечности:
.
Обратное, естественно, не верно. Члены последовательности могут иметь чередующиеся знаки. При этом предел может равняться бесконечности, но без определенного знака.

Заметим также, что если какое-то свойство выполняется для произвольной последовательности с пределом равным бесконечности, то это же свойство выполняется и для последовательности, чей предел равен плюс или минус бесконечности.

Окрестности бесконечно удаленных точек

Когда мы рассматривали конечные пределы, то ввели понятие окрестности точки. Напомним, что окрестностью конечной точки является открытый интервал, содержащий эту точку. Также мы можем ввести понятия окрестностей бесконечно удаленных точек.

Теперь мы можем дать единое определение предела последовательности, которое относится как к конечным, так и к бесконечным пределам.

Таким образом, если предел существует, то за пределами окрестности точки a может находиться только конечное число членов последовательности, или пустое множество. Это условие является необходимым и достаточным. Доказательство этого свойства, точно такое, как для конечных пределов.

С помощью логических символов существования и всеобщности, это определение запишется так:
.

Примеры бесконечно больших последовательностей

Все примеры Сначала мы рассмотрим три простых похожих примера, а затем решим более сложный.

Пользуясь определением бесконечно большой последовательности показать, что
⇓, ⇓, ⇓, ⇓.

Пример 1

Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.

Пример 2

Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.

Пример 3

Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.

Пример 4

Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Бесконечно малые и бесконечно большие последовательности

Бесконечно большие последовательности

Следствие. Любая бесконечно большая последовательность является неограниченной.

Замечание 2. Обратное утверждение в общем случае неверно.

является неограниченной, но не является бесконечно большой. Покажем это.

Бесконечно малые последовательности

Замечание 3. Любая бесконечно малая последовательность является ограниченной, но не наоборот.

Примеры решения задач

Задание	Доказать, что последовательность 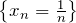является бесконечно малой.
Доказательство	Зададим произвольное положительное число и найдем такой номер 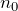элемента этой последовательности, что для всех выполняется соотношение

Что и требовалось доказать.

Источник

Последовательность

Последовательность
Нужно определить, является ли последовательность бесконечно большой, неограниченной, ограниченной.

Последовательность
Доказать что последовательность \sum_^\frac<1> расходится при помощи критерия Коши.

последовательность и ее подпоследовательности
существует например последовательность xn=\lg x * sin(\pi *x/2) предел ее подпоследовательность.

ограниченная последовательность
может ли быть ограниченной последовательностью сумма двух неограниченных последовательностей?

Допустим что выполняется условие 1).
1. Выберем M₁=1 и для него найдём n₁ такое что x_n1>M₁=1.
2. Следующее M₂ выбираем равное x_n1+1. Тогда опять же найдется n₂ такое что x_n2>M₂=2.
3. Следующее M₃ выбираем равное x_n2+1. Тогда опять же найдется n₃ такое что x_n3>M₃=3.
.
Таким образом, мы построили последовательность x_nk, k=1, 2, 3. которая является подпоследовательностью x_n и является бесконечно большой, потому что она больше чем бесконечно большая последовательность 1, 2, 3.

Для 2) и 3) доказательство аналогичное.

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Пределы и Последовательность
Здравствуйте, я списал с доски решение профессора, и не могу понять, что за трюк. У меня другой.

Источник

Бесконечно малые и бесконечно большие последовательности.

Бесконечно малые последовательности.

Последовательность \(\<\alpha_\>\) называется бесконечно малой, если
$$
\displaystyle \lim_\alpha_=0.\nonumber
$$

При изучении свойств сходящихся последовательностей нам потребуется ввести арифметические операции над последовательностями. Назовем суммой, разностью, произведением и частным двух последовательностей \(\\>\) и \(\\>\) соответственно последовательности \(\+y_\>\), \(\-y_\>\), \(\y_\>\), \(\/y_\>\). При определении частного предполагается, что \(y_n\neq 0\) для всех \(n\in\mathbb\).

Бесконечно малые последовательности обладают следующими свойствами:

Так как бесконечно малая последовательность ограничена, то из доказанного свойства следует, что произведение конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Бесконечно большие последовательности.

Последовательность \(\\>\) называется бесконечно большой, если для любого \(\delta>0\) существует такой номер \(N_<\delta>\), что для всех \(n\geq N_<\delta>\) выполняется неравенство \(|x_|>\delta\). В этом случае пишут \(\displaystyle \lim_x_n=\infty\) и говорят, что последовательность имеет бесконечный предел.

Используя логические символы, это определение можно записать так:
$$
\displaystyle \ <\lim_x_=\infty\>\Leftrightarrow\forall\delta>0\ \exists N_<\delta>:\forall n\geq N_<\delta>\rightarrow|x_|>\delta.\label
$$
Дадим геометрическую интерпретацию определения \eqref. Назовем \(\delta\) — окрестностью \(\infty\) (рис. 5.1) множество \(E=\:|x|>\delta\>\). Если

Рис. 5.1

последовательность \(\\) имеет бесконечный предел, то в любой \(\delta\)-окрестности \(\infty\) лежат все члены последовательности, за исключением, быть может, конечного числа членов.

Аналогично вводятся для последовательности \(\\) понятия бесконечного предела, равного \(-\infty\) и \(+\infty\) Эти пределы обозначаются соответственно символами \(\undersetx_n=-\infty\) и определяются так:
$$
\<\undersetx_n=-\infty\>\Leftrightarrow\forall\delta>0 \ \exists N_<\delta>: \ \forall n\geq N_<\delta>\rightarrow x_ 0 \ \exists N_<\delta>: \ \forall n\geq N_<\delta>\rightarrow x_>\delta\label
$$

Множества \(E_1=\: \ x \delta\>\), где \(\delta > 0\), назовем \(\delta\)-окрестностями \(-\infty\) и \(+\infty\) соответственно (см. рис. 5.1). Тогда \(E=E_<1>\cup E_<2>\).

Согласно определению \eqref последовательность \(\\) имеет предел, равный \(+\infty\), если в \(\delta\)-окрестности символа \(+\infty\) содержатся все члены этой последовательности, за исключением, быть может, конечного числа их. Аналогичный смысл имеет определение \eqref.

В дальнейшем под пределом последовательности будем понимать конечный предел, если не оговорено противное.

Приведем примеры последовательностей, имеющих бесконечный предел:

Источник

Подпоследовательности и частичные пределы последовательностей

Определение подпоследовательности

Свойства подпоследовательностей

Свойство 3 является следствием свойств 1 и 2.

Частичный предел последовательности

Произвольная последовательность может иметь конечное или бесконечное число частичных пределов ⇑.

5. Свойство частичного предела последовательности
Точка является частичным пределом последовательности тогда и только тогда, когда в любой окрестности точки a содержится бесконечное число членов последовательности.
Доказательство ⇓

Верхний и нижний частичные пределы

Рассмотрим множество частичных пределов последовательности. Эта теорема утверждает, что верхняя и нижняя грани этого множества являются ее элементами. То есть множество частичных пределов последовательности замкнуто, оно содержит свою границу. Для произвольного множества это может не выполняться. Например, для открытого интервала не существует наибольшего и наименьшего элемента, поскольку и верхняя грань b и нижняя a не принадлежит этому множеству.

Если последовательность не ограничена сверху, то ее верхний частичный предел равен плюс бесконечности:
.
Соответственно, если последовательность не ограничена снизу, то
.

Если последовательность ограничена, то ее верхний и нижний частичные пределы конечны.

8. Теорема о неравенстве между верхним и нижним частичными пределами
Верхний и нижний частичные пределы последовательности удовлетворяют неравенству:
.
Частичные пределы равны друг другу тогда и только тогда, когда существует предел последовательности:
.
Доказательство ⇓

9. Связь верхних и нижних пределов между последовательностями n> и <–x_n>.
Имеет место очевидное равенство:
.

10. Свойства верхних и нижних пределов суммы последовательностей
Верхний и нижний частичные пределы от суммы последовательностей удовлетворяют следующим неравенствам:
;
,
где последовательности и ограничены.
Доказательство ⇓

11. Свойство верхних пределов произведения последовательностей
Пусть последовательность сходится к конечному положительному числу:
.
И пусть – любая последовательность. Тогда
.
Отсюда
.
Доказательство ⇓

Применяя равенство
,
можно получить другие подобные соотношения.

Доказательство свойств и теорем

Далее перечислены определения и свойства, которые мы будем использовать при доказательстве свойств подпоследовательностей.

1. Свойство подпоследовательностей сходящейся последовательности

2. Свойство последовательности, все подпоследовательности которой сходятся к одному числу

5. Свойство частичного предела последовательности

Все свойства ⇑ Точка является частичным пределом последовательности тогда и только тогда, когда в любой окрестности точки a содержится бесконечное число членов последовательности.

Возьмем произвольную окрестность точки a : ⇑. В качестве первого члена подпоследовательности возьмем любой член последовательности, принадлежащий этой окрестности.

6. Теорема о существовании верхнего и нижнего частичных пределов

В этом случае точка является верхним частичным пределом последовательности.

Пусть последовательность ограничена сверху и при этом любой отрезок содержит только конечное число членов последовательности.

Поскольку мы выбирали самые правые отрезки с бесконечным числом членов, то точка c является верхним частичным пределом последовательности.

7. Свойство верхнего и нижнего частичных пределов

8. Теорема о неравенстве между верхним и нижним частичными пределами

Все свойства ⇑ Верхний и нижний частичные пределы последовательности удовлетворяют неравенству:
.
Частичные пределы равны друг другу тогда и только тогда, когда существует предел последовательности:
.

10. Свойства верхних и нижних пределов суммы последовательностей

Все свойства ⇑ Верхний и нижний частичные пределы от суммы последовательностей удовлетворяют следующим неравенствам:
;
,
где последовательности и ограничены.

Докажем второе неравенство:
.
Умножим первое неравенство на – 1 :
.
Применим свойство 8 ⇑:
.

11. Свойство верхних пределов произведения последовательностей

Все свойства ⇑ Пусть последовательность сходится к конечному положительному числу:
.
И пусть – любая последовательность. Тогда
.
Отсюда
.

Из (10.1) и (10.2) следует, что
.
Свойство доказано.

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник