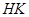Доказать что ядро гомоморфизма является нормальной подгруппой

18.04.202223.04.2022 admin 0 Comments

Гомоморфизм групп

Из Википедии — свободной энциклопедии

В математике, если заданы две группы (G, ∗) и (H, •), гомоморфизм групп из (G, ∗) в (H, •) — это функция h : G → H, такая, что для всех u и v из G выполняется

где групповая операция слева от знака «=» относится к группе G, а операция справа относится к группе H.

Отсюда можно вывести, что h отображает нейтральный элемент e_G группы G в нейтральный элемент e_H группы H, а также отображает обратные элементы в обратные в том смысле, что

Таким образом, можно сказать, что h «сохраняет групповую структуру».

В более ранних работах h(x) могло обозначаться как x_h, хотя это может привести к путанице с индексами. В последнее время наметилась тенденция опускать скобки при записи гомоморфизма, так что h(x) превращается просто в x h. Эта тенденция особенно заметна в областях теории групп, где применяется автоматизация, поскольку это лучше согласуется с принятым в автоматах чтении слов слева направо.

В областях математики, где группы снабжаются дополнительными структурами, гомоморфизм иногда понимается как отображение, сохраняющее не только структуру группы (как выше), но и дополнительную структуру. Например, гомоморфизм топологических групп часто предполагается непрерывным.

Источник

Группы

Примеры 1.9.17 (примеры подгрупп).

Замечание 1.9.21. Любая циклическая группа G=(a) является конечной или счетной коммутативной группой. Поэтому любая некоммутативная группа не является циклической и любая несчетная группа не является циклической группой.

Упражнение 1.9.25. В рассмотренных выше примерах найти образ и ядро гомоморфизма.

Задача 1.9.26. Доказать, что не существует сюръективного гомоморфизма .

Указание. В (Q,+) уравнение nx=a имеет (и единственное) решение для любых , .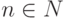

Группы G и G’ называются изоморфными если существует какой-либо изоморфизм 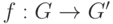(обозначение ).,

Следствие 1.9.33. Отношение является отношением эквивалентности на классе групп.

Замечание 1.9.34. Изоморфные группы обладают одинаковыми «алгебраическими» свойствами.

Источник

Теоремы о гомоморфизмах

Пусть G – группа и P – другая группа. Пусть каждому элементу a Î G сопоставлен некоторый элемент из S, то есть, дано отображение G и S. Отображение φ называется гомоморфным или гомоморфизмом G в S, если произведение элементов из G соответствует произведение их образов, то есть

Предложение 1.5.1.Гомоморфным образом φ(G) группы G является группой. Образом единицы группы G является единица образа, и взаимно обратным элементом G соответствуют взаимно обратные образы.

Гомоморфизм G в S, при котором различным элементам из G сопоставляется различные элементы в S.

Всякое изоморфное отображение группы G на себя называется автоморфизмом. Если в группе G выбран некоторый элемент а, то отображение, переводящее всякий элемент х этой группы в элемент

а –1 ха, то есть трансформирование всей группы элементов а, будет автоморфизмом группы G. Действительно, из а – 1 ха=а – 1 ya следует x = y, то есть отображение взаимно однозначно. Равенство х=а – 1 (аха – 1 )а

показывает, что при этом отображении всякий элемент группы будет образом некоторого элемента. Из соотношения a –1 xa· a –1 ya = a –1 (xy)a

следует изоморфизм рассматриваемого отображения. Такой автоморфизм группы G называется её внутренним автоморфизмом.

Пусть φ – гомоморфное отображение группы G на группу S. Множество всех элементов из G, имеющих один и тот же образ х Î S, называется полным прообразом элемента х и обозначается φ –1 (х). Полный прообраз единицы группы S называется ядром гомоморфизма.

Предложение 1.5.2. Ядро гомоморфизма φ группы G на группу S является нормальной подгруппой группы G.

Доказательство. Введем обозначение H для ядра. Если a Î H, то

Предложение 1.5.3.В условиях предложения 1.5.2. полные прообразы элементов из S является классами смежности по ядру гомоморфизма.

Теорема 1.5.4. (первая теорема о гомоморфизме) Гомоморфный образ группы изоморфен её факторгруппе по ядру гомоморфизма.

Доказательство. Между образами при гомоморфизме и элементами факторгруппы имеется взаимно однозначное соответствие, в силу предложения 1.5.3. Оно сохраняется при умножении, ибо

Остается доказать любая ли нормальная подгруппа может быть принята за ядро гомоморфизма. Ответ положительный, так как отображение группы G на факторгруппу G / H по нормальной подгруппе H, заключающиеся в том, что каждому элементу группы G сопоставляется содержащий его класс смежности, есть гомоморфизм, и его ядро совпадает с H (это следует из определения умножение классов смежности как элементов факторгруппы). ■

Предложение 1.5.5. H и K подгруппы группы G и , тогда является подгруппой группы , и .

, причем , так как поэтому, таким образом, для каждого элемента существует обратный .

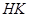
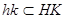
Пусть , причем , тогда

где и поэтому , то есть условие замкнутости выполняется, таким образом, в силу предложения 1.1.1. можем считать, что HK является подгруппой группы G.

Теорема 1.5.6 (об изоморфизме). Пусть G – группа и H и K две его подгруппы. Причём 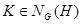тогда и .

Доказательство. Покажем что подгруппа нормальна в K . Тогда для : , так как и , и по условию , следовательно, для любого k из K и значит . Кроме, того, по предыдущему предложению имеем HK = KH подгруппа группы G и .

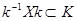
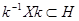
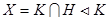
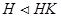
Существует сюръективный гомоморфизм , сопоставленный каждому смежный класс группы по подгруппе H. Несложно видеть является ядром гомоморфизма, таким образом, по теореме 1.5.4. получаем: