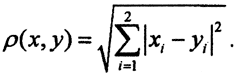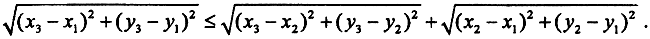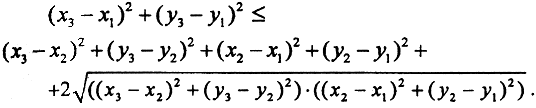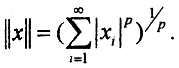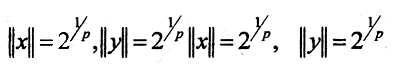Доказать что является метрикой

Теория функций действительного переменного/Метрическое пространство

В основе математического анализа лежит понятие предела числовой последовательности и операция предельного перехода. Достаточно сказать, что производная и определённый интеграл определяются через понятие предела. При определении предела используется тот факт, что на числовой прямой определено расстояние между вещественными числами. Но оказывается, что для формулировки многих фундаментальных понятий и доказательства различных теорем анализа важна не природа действительных чисел, а только само понятие расстояния. Обобщением представления о расстоянии между действительными числами на случай произвольного множества является понятие метрики, которое мы сейчас введём.

Содержание

Определение метрического пространства [ править ]

Пусть M — некоторое непустое множество, ρ — некое отображение, ставящие в соответствие двум элементам множества M некоторое вещественное число:

отображение ρ называется метрикой, если оно обладает следующими свойствами (аксиомы метрики):

\rho (x,y)\leq \rho (x,z)+\rho (z,y)>.

Совокупность множества M и определённой на нём метрики ρ называют метрическим пространством и обозначают (M,ρ). Иногда, особенно когда из контекста понятно о какой метрике идёт речь, метрическое пространство обозначают так же, как и само множество М. Элементы метрического пространства обычно называют точками.

Одним из простейших (и важнейших) примеров метрического пространства является числовая прямая. Покажем, что множество вещественных чисел с метрикой ρ(x, y)=|х — у| является метрическим пространством. Действительно, рассмотрим три произвольных вещественных числа

Все аксиомы метрического пространства выполняются, по свойствам модуля:

|x-y|=0\Leftrightarrow x=y> , | x − y | = | − ( y − x ) | = | − 1 | ⋅ | y − x | = | y − x | <\displaystyle

|x-y|=|-(y-x)|=|-1|\cdot |y-x|=|y-x|> , | x − y | = | x − z + z − y | ≤ | x − z | + | z − y | <\displaystyle

|x-y|=|x-z+z-y|\leq |x-z|+|z-y|> .

Пусть (M, ρ) — метрическое пространство, и A — непустое подмножество множества M, тогда (A, ρ) — тоже является метрическим пространством, которое называется подпространством метрического пространства (M,ρ).

Например, множество рациональных чисел является подмножеством действительных чисел:

а следовательно, если взять естественную для вещественных чисел метрику

будет метрическим пространством.

В принципе, любое множество можно рассматривать как метрическое пространство. Действительно, если для элементов произвольного множества ввести так называемую дискретную метрику:

то получится метрическое пространство, которое называют пространством изолированных точек.

На одном и том же множестве можно задавать различные метрики (ниже дан пример), однако не следует считать, что метрику можно задавать произвольно. Дело в том, что при решении практических задач метрика, как правило, является частью постановки задачи.

Свойства метрики [ править ]

Рассмотрим некоторые свойства метрики, которые могут быть выведены из её определения.

Свойство 1. Метрика является неотрицательной функцией:

По аксиоме тождества

\forall x\in M:\rho (x,x)=0> .

С другой стороны, по аксиоме треугольника:

\forall y\in M:\rho (x,x)\leq \rho (x,y)+\rho (y,x)> .

В силу аксиомы симметрии:

\rho (x,y)=\rho (y,x)> ,

Откуда и получается, что

Свойство 2 (Неравенство многоугольника). Для любой конечной системы элементов

множества M имеет место неравенство

Доказательство проводится с помощью метода математической индукции, база индукции — аксиома треугольника.

Но по предположению:

Свойство 3 (Неравенство четырёхугольника). Для любых четырёх элементов

имеет место неравенство

Сравнивая два эти неравенства, получим

Свойство 3а (Второе неравенство треугольника). Для любых трёх элементов

имеет место неравенство

Важные неравенства [ править ]

Для проверки аксиомы треугольника для различных пространств полезны следующие леммы.

Лемма 1 (неравенство Коши-Буняковского):

| ∑ i = 1 n a i b i | ≤ ∑ i = 1 n a i 2 ⋅ ∑ i = 1 n b i 2 <\displaystyle \left|\sum _^a_b_\right|\leq <\sqrt <\sum _^a_^<2>>>\cdot <\sqrt <\sum _^b_^<2>>>> .

F ( t ) = ∑ i = 1 n ( a i t + b i ) 2 ≥ 0 <\displaystyle F(t)=\sum _^(a_t+b_)^<2>\geq 0> .

Применим формулу квадрата суммы:

F ( t ) = t 2 ∑ i = 1 n a i 2 + 2 t ∑ i = 1 n a i b i + ∑ i = 1 n b i 2 <\displaystyle F(t)=t^<2>\sum _^a_^<2>+2t\sum _^a_b_+\sum _^b_^<2>> .

Пусть сначала все a i <\displaystyle a_> равны нулю. В этом случае

Теперь будем считать, что

D = 4 ( ∑ i = 1 n a i b i ) 2 − 4 ∑ i = 1 n a i 2 ∑ i = 1 n b i 2 <\displaystyle D=4\left(\sum _^a_b_\right)^<2>-4\sum _^a_^<2>\sum _^b_^<2>> ,

( ∑ i = 1 n a i b i ) 2 − ∑ i = 1 n a i 2 ∑ i = 1 n b i 2 ≤ 0 <\displaystyle \left(\sum _^a_b_\right)^<2>-\sum _^a_^<2>\sum _^b_^<2>\leq 0>

( ∑ i = 1 n a i b i ) 2 ≤ ∑ i = 1 n a i 2 ∑ i = 1 n b i 2 <\displaystyle \left(\sum _^a_b_\right)^<2>\leq \sum _^a_^<2>\sum _^b_^<2>> .

Лемма 2 (неравенство Минковского):

∑ i = 1 n ( a i + b i ) 2 ≤ ∑ i = 1 n a i 2 + ∑ i = 1 n b i 2 <\displaystyle <\sqrt <\sum _^(a_+b_)^<2>>>\leq <\sqrt <\sum _^a_^<2>>>+<\sqrt <\sum _^b_^<2>>>> .

По формуле квадрата суммы и в силу неравенства Коши-Буняковского:

∑ i = 1 n ( a i + b i ) 2 = ∑ i = 1 n a i 2 + 2 ∑ i = 1 n a i b i + ∑ i = 1 n b i 2 ≤ ∑ i = 1 n a i 2 + 2 ∑ i = 1 n a i 2 ⋅ ∑ i = 1 n b i 2 + ∑ i = 1 n b i 2 <\displaystyle \sum _^(a_+b_)^<2>=\sum _^a_^<2>+2\sum _^a_b_+\sum _^b_^<2>\leq \sum _^a_^<2>+2<\sqrt <\sum _^a_^<2>>>\cdot <\sqrt <\sum _^b_^<2>>>+\sum _^b_^<2>> .

Правая часть этого неравенства может быть записана в виде квадрата суммы:

∑ i = 1 n a i 2 + 2 ∑ i = 1 n a i 2 ∑ i = 1 n b i 2 + ∑ i = 1 n b i 2 = ( ∑ i = 1 n a i 2 + ∑ i = 1 n b i 2 ) 2 <\displaystyle \sum _^a_^<2>+2<\sqrt <\sum _^a_^<2>>><\sqrt <\sum _^b_^<2>>>+\sum _^b_^<2>=\left(<\sqrt <\sum _^a_^<2>>>+<\sqrt <\sum _^b_^<2>>>\right)^<2>> .

∑ i = 1 n ( a i + b i ) 2 ≤ ( ∑ i = 1 n a i 2 + ∑ i = 1 n b i 2 ) 2 <\displaystyle \sum _^(a_+b_)^<2>\leq \left(<\sqrt <\sum _^a_^<2>>>+<\sqrt <\sum _^b_^<2>>>\right)^<2>> .

Неравенство Минковского получается после извлечения квадратного корня из правой и левой части данного неравенства.

Лемма 3 (Интегральное неравенство Коши-Буняковского).

∫ a b f ( t ) g ( t ) d t ≤ ∫ a b f 2 ( t ) d t ⋅ ∫ a b g 2 ( t ) d t <\displaystyle \int \limits _^f(t)g(t)dt\leq <\sqrt <\int \limits _^f^<2>(t)dt>>\cdot <\sqrt <\int \limits _^g^<2>(t)dt>>> .

Рассмотрим неотрицательную функцию

F ( λ ) = ∫ a b [ f ( t ) λ + g ( t ) ] 2 d t <\displaystyle F(\lambda )=\int \limits _^[f(t)\lambda +g(t)]^<2>dt> .

По свойствам интеграла и формуле квадрата суммы:

F ( λ ) = λ 2 ∫ a b f 2 ( t ) d t + 2 λ ∫ a b f ( t ) g ( t ) d t + ∫ a b g 2 ( t ) d t <\displaystyle F(\lambda )=\lambda ^<2>\int \limits _^f^<2>(t)dt+2\lambda \int \limits _^f(t)g(t)dt+\int \limits _^g^<2>(t)dt> .

4 ( ∫ a b f ( t ) g ( t ) d t ) 2 − 4 ∫ a b f 2 ( t ) d t ⋅ ∫ a b g 2 ( t ) d t ≤ 0 <\displaystyle 4\left(\int \limits _^f(t)g(t)dt\right)^<2>-4\int \limits _^f^<2>(t)dt\cdot \int \limits _^g^<2>(t)dt\leq 0> ,

откуда и следует утверждение леммы.

Лемма 4 (Интегральное неравенство Минковского).

∫ a b [ f ( t ) + g ( t ) ] 2 d t ≤ ∫ a b f 2 ( t ) d t + ∫ a b g 2 ( t ) d t <\displaystyle <\sqrt <\int \limits _^[f(t)+g(t)]^<2>dt>>\leq <\sqrt <\int \limits _^f^<2>(t)dt>>+<\sqrt <\int \limits _^g^<2>(t)dt>>> .

По свойствам интеграла:

∫ a b [ f ( t ) + g ( t ) ] 2 d t = ∫ a b f 2 ( t ) d t + 2 ∫ a b f ( t ) g ( t ) d t + ∫ a b g 2 ( t ) d t <\displaystyle \int \limits _^[f(t)+g(t)]^<2>dt=\int \limits _^f^<2>(t)dt+2\int \limits _^f(t)g(t)dt+\int \limits _^g^<2>(t)dt>

Воспользуемся интегральным неравенством Коши-Буняковского:

∫ a b [ f ( t ) + g ( t ) ] 2 d t ≤ ∫ a b f 2 ( t ) d t + 2 ∫ a b f 2 ( t ) d t ⋅ ∫ a b g 2 ( t ) d t + ∫ a b g 2 ( t ) d t <\displaystyle \int \limits _^[f(t)+g(t)]^<2>dt\leq \int \limits _^f^<2>(t)dt+2<\sqrt <\int \limits _^f^<2>(t)dt>>\cdot <\sqrt <\int \limits _^g^<2>(t)dt>>+\int \limits _^g^<2>(t)dt> ,

∫ a b [ f ( t ) + g ( t ) ] 2 d t ≤ ( ∫ a b f 2 ( t ) d t + ∫ a b g 2 ( t ) d t ) 2 <\displaystyle \int \limits _^[f(t)+g(t)]^<2>dt\leq \left(<\sqrt <\int \limits _^f^<2>(t)dt>>+<\sqrt <\int \limits _^g^<2>(t)dt>>\right)^<2>> .

Интегральное неравенство Минковского получается после извлечения квадратного корня из правой и левой части данного неравенства.

Примеры метрических пространств [ править ]

Мы уже рассмотрели два метрических пространства: множество вещественных чисел и множество рациональных чисел. Ниже приведены ещё некоторые примеры метрических пространств, все они играют важную роль в математическом анализе и алгебре.

Проверка первых двух аксиом является, как правило, тривиальной задачей, основные трудности связаны с доказательством справедливости аксиомы треугольника.

Арифметическое евклидово пространство [ править ]

является метрическим пространством.

Перейдём к проверке третьей аксиомы.
3.

По неравенству Минковского (Лемма 2):

то есть аксиома действительно выполняется.

Метрика Хэмминга [ править ]

Метрика такого вида называется метрикой Хэмминга.

Равномерная метрика [ править ]

Таким образом, три рассмотренных примера показывают, что на основе одного и того же множество можно, задавая различные метрики, строить различные метрические пространства.

Комплексные числа [ править ]

является метрическим пространством. Справедливость аксиом следует из свойств модуля комплексного числа. Действительно, если z 1 = x 1 + i y 1 <\displaystyle z_<1>=x_<1>+iy_<1>> , а z 2 = x 2 + i y 2 <\displaystyle z_<2>=x_<2>+iy_<2>> , то

| z 1 − z 2 | = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 <\displaystyle |z_<1>-z_<2>|=<\sqrt <(x_<1>-x_<2>)^<2>+(y_<1>-y_<2>)^<2>>>> ,

таким образом, с точки зрения теории метрических пространств, множество комплексных чисел эквивалентно двумерному арифметическому евклидову пространству (геометрическая интерпретация комплексных чисел).

Непрерывные функции [ править ]

является метрическим пространством.

max x ∈ [ a ; b ] | f ( x ) − g ( x ) | = 0 <\displaystyle \max _|f(x)-g(x)|=0> ,

| f ( x ) − g ( x ) | ≤ max x ∈ [ a ; b ] | f ( x ) − g ( x ) | = 0 <\displaystyle |f(x)-g(x)|\leq \max _|f(x)-g(x)|=0> ,

Аксиома симметрии тоже выполняется.

Докажем теперь аксиому треугольника. Для любых трёх функций

в силу неравенства треугольника для модуля, выполняется неравенство

Возьмём максимальное значение левой и правой части:

max x ∈ [ a ; b ] | f ( x ) − g ( x ) | ≤ max x ∈ [ a ; b ] < | f ( x ) − h ( x ) | + | g ( x ) − h ( x ) | ><\displaystyle \max _|f(x)-g(x)|\leq \max _\left\<|f(x)-h(x)|+|g(x)-h(x)|\right\>> .

w 1 ( x ) + w 2 ( x ) ≤ max x ∈ [ a ; b ] w 1 ( x ) + max x ∈ [ a ; b ] w 2 ( x ) <\displaystyle w_<1>(x)+w_<2>(x)\leq \max _w_<1>(x)+\max _w_<2>(x)> ,

max x ∈ [ a ; b ] < w 1 ( x ) + w 2 ( x ) >≤ max x ∈ [ a ; b ] w 1 ( x ) + max x ∈ [ a ; b ] w 2 ( x ) <\displaystyle \max _\(x)+w_<2>(x)\>\leq \max _w_<1>(x)+\max _w_<2>(x)> ,

то есть наибольшее значение суммы функций не превосходит суммы их наибольших значений.

Используем последнее неравенство, положив

w_<2>(x)=|h(x)-g(x)|> ,

max x ∈ [ a ; b ] < | f ( x ) − h ( x ) | + | h ( x ) − g ( x ) | >≤ max x ∈ [ a ; b ] | f ( x ) − h ( x ) | + max x ∈ [ a ; b ] | h ( x ) − g ( x ) | <\displaystyle \max _\<<|f(x)-h(x)|+|h(x)-g(x)|>\>\leq \max _|f(x)-h(x)|+\max _|h(x)-g(x)|> .

Все аксиомы действительно выполняются.

На множестве непрерывных функций метрику можно определить иначе, например

полученное метрическое пространство обозначают C 2 [ a ; b ] <\displaystyle C_<2>[a;b]> .

Пространства числовых последовательностей [ править ]

Рассмотрим множество всевозможных числовых последовательностей вида

Если на этом множестве ввести расстояние

то получим метрическое пространство, которое обозначают l 2 <\displaystyle l_<2>> . Ряд

∑ k = 1 ∞ ( x k − y k ) 2 <\displaystyle \sum _^<\infty >(x_-y_)^<2>>

сходится, если сходятся ряды

\sum _^<\infty >y_^<2>> ,

а значит введённая метрика имеет смысл для любых последовательностей из l 2 <\displaystyle l_<2>> .

Доказательство аксиом тождества и симметрии не представляет труда, доказательство справедливости аксиомы треугольника для указанной метрики можно с помощью предельного перехода в неравенстве Минковского.

Выводы [ править ]

Приведённые примеры показывают, что понятия метрики и метрического пространства позволяют рассматривать с единых позиций такие непохожие на первый взгляд объекты, как вещественные и комплексные числа, вектора, непрерывные функции и числовые последовательности.

Источник

СОДЕРЖАНИЕ

Определение

Метрика называется ультраметрикой, если она удовлетворяет следующей более сильной версии неравенства треугольника, когда точки никогда не могут попадать «между» другими точками:

Метрика d на группе G (записанная мультипликативно) называется левоинвариантной (соответственно правоинвариантной ), если мы имеем

Примечания

Примеры

Эквивалентность показателей

Для данного множества X две метрики d ₁ и d ₂ называются топологически эквивалентными ( равномерно эквивалентными ), если тождественное отображение

Метрика, индуцированная нормой

Нормы на векторных пространствах эквивалентны определенным метрикам, а именно однородным, трансляционно-инвариантным. Другими словами, каждая норма определяет метрику, а некоторые метрики определяют норму.

Точно так же полунорма индуцирует псевдометрику (см. Ниже), а однородная псевдометрика, инвариантная относительно сдвигов, индуцирует полунорму.

Метрики на мультимножествах

Обобщенные метрики

Расширенные метрики

Псевдометрика

Квазиметрики

Иногда квазиметрика определяется как функция, удовлетворяющая всем аксиомам метрики, за исключением, возможно, симметрии. Название этого обобщения не совсем стандартизировано.

Квазиметрику вещественных чисел можно определить, задав

Метаметрики

В метаметрике выполняются все аксиомы метрики, за исключением того, что расстояние между идентичными точками не обязательно равно нулю. Другими словами, аксиомы метаметрики:

Полиметрика

Некоторые авторы работают с более слабой формой неравенства треугольника, например:

Преметрики

Это нестандартный термин. Иногда он используется для обозначения других обобщений показателей, таких как псевдосемиметрика или псевдометрика; в переводах русских книг иногда встречается как «праметрический». Его еще называют дистанцией.

Это определяет преметрику на множестве степеней преметрического пространства. Если мы начнем с (псевдополеметрического) пространства, мы получим псевдосемиметрику, то есть симметричную преметрику. Любая преметрика приводит к следующему оператору предварительного закрытия cl :

Псевдоквазиметрия

Расстояние Лукашика-Кармовского

Важные случаи обобщенных показателей

Источник

Доказать что является метрикой

1.4.3. Стандартные метрические пространства

Пример 1. На плоскости R 2 для точек A(x₁, y₁) и B(x₂, y₂) определим расстояние тремя различными способами и покажем, что введенные расстояния являются метриками, то есть проверим выполнимость аксиом.

1.Метрика 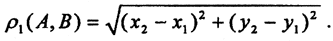. Это евклидова метрика при p = 2

Первые аксиомы очевидны. Проверим третью аксиому. Рассмотрим точки A(x₁, y₁), B(x₂, y₂) и C(x₃, y₃) докажем следующее неравенство:

Возведем это неравенство в квадрат:

Так как (x₃-x₁) 2 ≤(x₃-x₂) 2 +(x₂-x₁) 2 и (y₃-y₁) 2 ≤(y₃-y₂) 2 +(y₂-y₁) 2 (поскольку (b-a) 2 )≤b 2 +a 2 ) и выражение 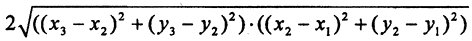неотрицательно, то неравенство является верным.

2. Метрика ρ₂(A,B) = max<|y₂-y₁|, |x₂-x₁|>. Это двумерное арифметическое пространство с супремальной метрикой. Первые аксиомы очевидны. Проверим третью аксиому.

( Комментарий. 1. Понятие пополнения употреблено впрок и будет определено позднее.

2. Любое нормированное пространство является метрическим с метрикой ρ = ||x-y||. Выполнение первых аксиом очевидно. Третья выполняется в силу ||x-y||=||(x-z)+(z-y)||≤||x-z||+||z-y||. Обратное, вообще говоря, неверно, то есть метрические пространства, вообще говоря, не являются нормированными. Но если потребовать, чтобы метрическое пространство обладало инвариантностью относительно сдвигов, то есть ρ(x+z,y+z) = ρ(x,y) и однородностью относительно растяжений, то есть ρ(αx,αy) = |α|ρ(x,y), то тогда верно и обратное, и норма элемента есть метрика, второй элемент которой есть ноль.

Для стандартных метрических пространств это так, так что все вышеприведённые примеры являются одновременно и примерами стандартных норм с геометрией, отличной от эвклидовой. Единичные шары в этих метриках изображены в примере 3.)

Пример 2. Покажем, что ρ = arctg|x-y| является метрикой. Выполнение первых двух аксиом метрики очевидно. Чтобы проверить третью, то есть arctg|x-z+z-y|≤arctg|x-z|+arctg|z-y|, докажем, что для любых α,β ≥0имеет место неравенство arctg(α+β)≤arctgα+arctgβ.

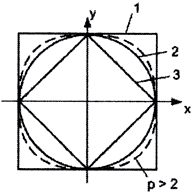
Пример 3. Рассмотрим пространство R 2 _p. Положив y = 0, а ρ = 1, мы получим единичную сферу в пространстве R 2 _p.

При p = 1 уравнение этой сферы имеет вид ||x||₁ = |x|+|y| = 1, и такая метрика называется октаэдрической, потому что единичной сферой в трёхмерном случае ||x||₁ = |x|+|y|+|z| = 1 будет октаэдр.

При p = 2 уравнение этой сферы имеет вид 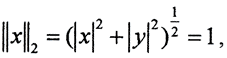и такая метрика называется евклидовой (сферической), потому что единичной сферой в трёхмерном случае будет обычная сфера.

Чебышёвская (кубическая) метрика: ||x||_∞ = max<|x|,|y|>, потому что единичной сферой в трёхмерном случае ||x||_∞ = max <|x|,|y|,|z|>= 1 будет куб.

Пусть неверно, что ρ(x,y)≤ρ(x,z)+ρ(z,y). Тогда ρ(x,y) = 1.⇒x ≠y. Но тогда ρ(x,z)+ρ(z,y) = 0, то есть x=y.

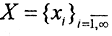
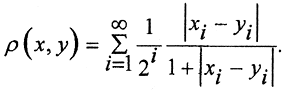
2. Ограниченные последовательности с метрикой Проверим третью аксиому.

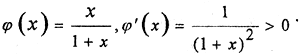
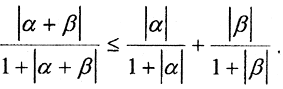
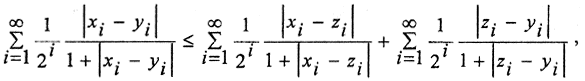
Рассмотрим возрастающую функцию Так как |α+β|≤|α|+|β|, то φ(|α+β|)≤φ(|α|)+φ(|β|), то есть Пусть α = x_i-z_i, β = z_i-y_i, тогда α+β = x_i-y_i. Теперь или ρ(x,y)≤ρ(x,z)+ρ(z,y).

В этой метрике при m ρ(m, n₂) то есть натуральные числа, чем дальше они расположены на числовой оси, тем ближе по метрике ρ.

Ясно, что равенство параллелограмма не выполнено при p≠2.

5. Покажем, что пространство C[0,1] не гильбертово.

Пространство C[0,1] полное нормированное пространство, то есть банахово. (Полноту покажем в следующем пункте.) Уже отмечалось, что норма порождается скалярным произведением, если и только если выполняется равенство параллелограмма ||x+y|| 2 +||x-y|| 2 = 2(||x|| 2 +||y|| 2 ). Пусть x(t) = 1, y(t) = t. Тогда, вычисляя норму в пространстве C[0,1], сразу получим ||t+1|| 2 +||t-1|| 2 = 2 2 +1 2 ≠2(1 2 +1 2 ).

6. Будет ли нормированным пространством линейное пространство непрерывно дифференцируемых функций, если на нём в качестве нормы использовать норму пространства непрерывных функций C[0,1]?

Да. Проверим аксиоматику:

3)||x(t)+y(t)||_t∈[a,b] = max_t∈[a,b]|x(t)+y(t)|≤ max_t∈[a,b](|x(t)|+|y(t)|)≤ max_t∈[a,b]|x(t)|+max_t∈[a,b]|y(t)| = ||x(t)||_t∈[a,b]+||y(t)||_t∈[a,b].

7. Будет ли нормированным пространством линейное пространство непрерывно дифференцируемых функций, если на нём в качестве нормы использовать норму ||x(t)||_t∈[a,b] = max_t∈[a,b]|x'(t)|?

8. Доказать, что подпространство B₁ банахова пространства B является банаховым пространством.

Источник