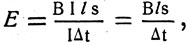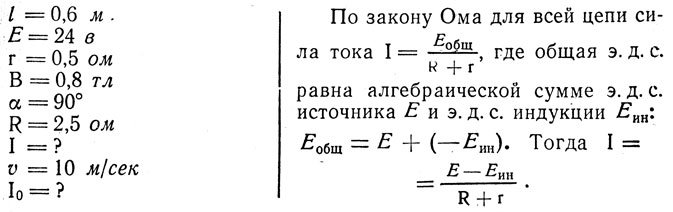F ibl sin альфа что за формула
Закон Ампера
Закон Ампера показывает, с какой силой действует магнитное поле на помещенный в него проводник. Эту силу также называют силой Ампера.
Ампер первым установил, что проводники, по которым течет электрический ток, взаимодействуют механически (притягиваются или отталкиваются).
Конкретное направление силы Ампера можно найти с помощью правила левой руки. Левую руку надо расположить так, чтобы линии поля входили в ладонь, четыре пальца были направлены по току, тогда отогнутый на 90 градусов большой палец укажет направление силы Ампера.
Еще Ампер установил, что два параллельных проводника с током притягиваются, если токи имеют одинаковые направления и отталкиваются, если токи текут в противоположные стороны. Это просто объяснить, если представить, что один проводник создает магнитное поле, а другой проводник в него помещен и это поле действует на него. Можно использовать правило левой руки и выяснить, как направлена сила.
Закон Ампера
Сила Ампера – сила, действующая на проводник тока, находящийся в магнитном поле и равная произведению силы тока в проводнике, модуля вектора индукции магнитного поля, длины проводника и синуса угла между вектором магнитного поля и направлением тока в проводнике.
Для прямолинейного проводника сила Ампера имеет вид:
Этой формулой можно пользоваться:
Если размер проводника произволен, а поле неоднородно, то формула выглядит следующим образом:
Значение закона Ампера
На основании закона Ампера устанавливают единицы силы тока в системах СИ и СГСМ. Так как ампер равен силе постоянного тока, который при течении по двум параллельным бесконечно длинным прямолинейным проводникам бесконечно малого кругового сечения, находящихся на расстоянии 1м друг от друга в вакууме вызывает силу взаимодействия этих проводников равную \( 2\cdot <10>^<-7>Н \) на каждый метр длины.
Ток в один ампер – это такой ток, при котором два однородных параллельных проводника, расположенные в вакууме на расстоянии один метр друг от друга взаимодействуют с силой \( 2\cdot <10>^ <-7>\) Ньютона.
Закон взаимодействия токов – два находящихся в вакууме параллельных проводника, диаметры которых много меньше расстояний между ними, взаимодействуют с силой прямо пропорциональной произведению токов в этих проводниках и обратно пропорциональной расстоянию между ними.
Электродинамика (страница 2)
Два незаряженных электрометра соединили проводящим металлическим стержнем с изолирующей ручкой. Затем к первому поднесли отрицательно заряженную палочку, не касаясь шара. После этого сначала убрали стержень, соединяющий электрометры, а только потом убрали заряженную палочку. Объясните наблюдаемые явления и определите знак заряда на электрометрах после того, как убрали стержень и палочку.

Источник: ЕГЭ по физике 07.06.2017. Основная волна
При поднесении отрицательно заряженной палочки к электрометру произойдет перераспределение зарядов. Ближайший электрометр будет иметь положительный заряд, а дальний будет иметь отрицательный заряд. Так как разноименные заряды притягиваются, а одноименные отталкиваются. Так как сначала удаляют соединяющий стержень, то электрометры в конце концов сохранят свои заряды, то есть ближний к палочке будет заряжен положительно, дальний – отрицательно.
Около небольшой металлической пластины, укрепленной на изолирующей подставке, подвесили на шёлковой нити лёгкую металлическую незаряженную гильзу. Когда пластину подсоединили к клемме высоковольтного выпрямителя, подав на неё отрицательный заряд, гильза пришла в движение. Опишите движение гильзы и объясните его.
Под действием электрического поля пластины изменится распределение электронов в гильзе и произойдёт её электризация: та её сторона, которая ближе к пластине, будет иметь положительный заряд, а противоположная сторона — отрицательный.
Поскольку силы взаимодействия заряженных тел уменьшаются с ростом расстояния между ними, притяжение к пластине левой стороны гильзы будет сильнее отталкивания правой стороны гильзы, и гильза будет двигаться к пластине, пока не коснется её.
В момент касания часть электронов перейдет с отрицательно заряженной пластины на гильзу, гильза приобретет отрицательный заряд и оттолкнется от одноименно заряженной пластины. Гильза отклонится вправо и зависнет в положении, в котором равнодействующая всех сил равна нулю.
К колебательному контуру подсоединили источник тока, на клеммах которого напряжение гармонически меняется с частотой \(\nu\) Индуктивность \(L\) катушки колебательного контура можно плавно менять от максимального значения \(L_
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Дальний Восток.
В колебательном контуре возбуждаются колебания. Частота этих колебаний находится по формуле: \[\nu_0=\dfrac<1><2\pi \sqrt
В нашем случае ученик изменяет частоту колебаний от \(\nu_<0min>=\dfrac<1><2\pi \sqrt
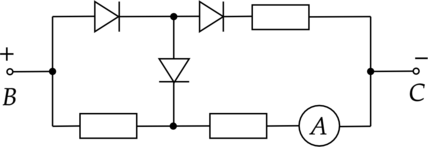
Три одинаковых резистора и три одинаковых идеальных диода включены в электрическую цепь, показанную на рисунке, и подключены к аккумулятору в точках В и С. Показания амперметра равны 2 А. Определите силу тока через амперметр после смены полярности подключения аккумулятора. Нарисуйте эквивалентные электрические схемы для двух случаев подключения аккумулятора. Опираясь на законы электродинамики, поясните свой ответ. Сопротивлением амперметра и внутренним сопротивлением аккумулятора пренебречь.
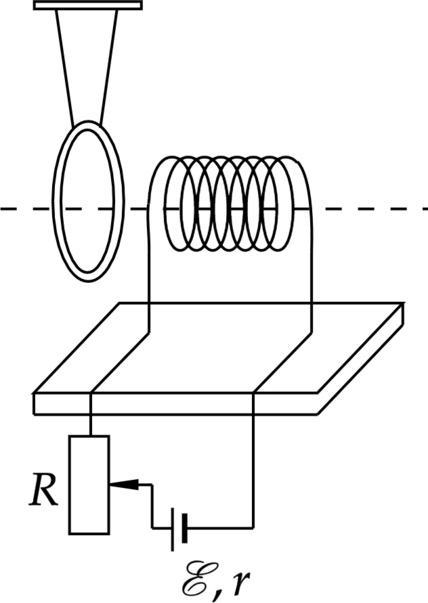
Многовитковая катушка медного провода подключена к источнику тока через реостат. Вблизи торца катушки на шёлковых нитях подвешено замкнутое медное кольцо с малым сопротивлением. Ось кольца совпадает с осью катушки (см. рисунок). Опишите, как начнёт двигаться кольцо (притянется, оттолкнётся или останется неподвижным относительно катушки), если движок реостата резко сдвинуть вверх в крайнее положение. Ответ поясните, указав, какие физические явления и закономерности Вы использовали для объяснения.
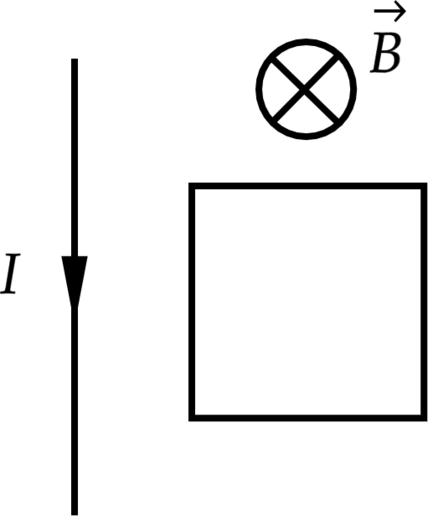
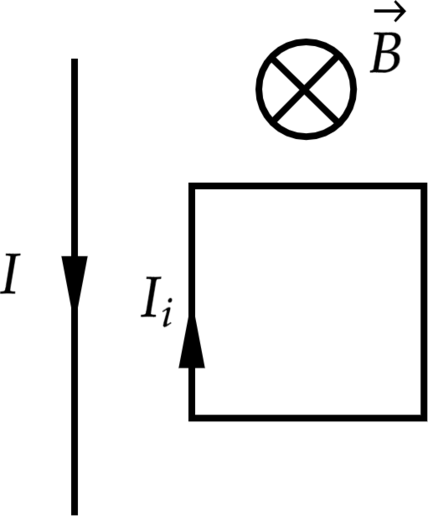
Прямолинейный проводник с током и проводящая рамка лежат в плоскости, перпендикулярной линиям индукции однородного магнитного поля. Опираясь на законы физики, укажите направление силы, действующей на рамку, когда величина магнитной индукции B уменьшается.
3. Направление линий индукции поля, создаваемого проводником с током, в каждой точке рамки одинаково, оно определяется по правилу буравчика. В проводнике протекает постоянный ток, поэтому поле проводника постоянно и не влияет на индукционный ток в рамке.
4. В магнитном поле проводника на каждую сторону рамки действует сила Ампера. Стороны рамки, перпендикулярные проводнику, расположены на одинаковом расстоянии от проводника. На них действуют силы, равные по модулю и направленные противоположно друг другу. Их сумма равна нулю. Силы, действующие на параллельные проводнику стороны рамки, направлены тоже противоположно друг другу. Из-за неоднородности поля проводник с током отталкивает ближнюю сторону рамки сильнее, чем притягивает более удалённую от него сторону. Результирующая этих сил отталкивает рамку от проводника.
5. Согласно принципу суперпозиции, однородное магнитное поле и поле проводника с током действуют на рамку независимо друг от друга. Поэтому результирующая сил, приложенных к рамке, направлена вправо от проводника с током.
F ibl sin альфа что за формула
§ 98. Электродвижущая сила индукции в прямолинейном проводнике
При движении прямолинейного проводника в магнитном поле на концах проводника возникает э. д. с. индукции. Ее можно вычислить не только по формуле 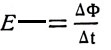
индукции в прямолинейном проводнике. Она выводится так. Приравняем формулы (1) и (2) § 97:
где s /Δt = v есть скорость перемещения проводника. Поэтому э. д. с. индукции при движении проводника перпендикулярно к силовым линиям магнитного поля
Рис. 148. К выводу формулы э. д. с. индукции в прямолинейном проводнике
Если проводник движется со скоростью v (рис. 148, а), направленной под углом α к линиям индукции, то скорость v разлагается на составляющие v1 и v2. Составляющая направлена вдоль линий индукции и при движении проводника не вызывает в нем э. д. с. индукции. В проводнике э. д. с. индуктируется только за счет составляющей v2 = v sin α, направленной перпендикулярно к линиям индукции. В этом случае э. д. с. индукции будет
Это и есть формула э. д. с. индукции в прямолинейном проводнике.
Итак, при движении прямолинейного проводника в магнитном поле в нем индуктируется э. д. с., величина которой прямо пропорциональна активной длине проводника и нормальной составляющей скорости его движения.
То, что э. д. с. индукции зависит от скорости v вращения рамки и от индукции В магнитного поля, можно видеть на таком опыте (рис. 148, б). При медленном вращении якоря генератора тока лампочка горит тускло: возникла малая э. д. с. индукции. При увеличении скорости вращения якоря лампочка горит ярче: возникает большая э. д. с. индукции. При той же скорости вращения якоря удалим один из магнитов, уменьшив тем самым индукцию магнитного поля. Лампочка горит тускло: э. д. с. индукции уменьшилась.
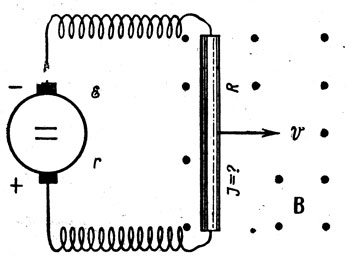
Задача 35. Прямолинейный проводник длиной 0,6 м гибкими проводниками присоединен к источнику тока, э. д. с. которого 24 в и внутреннее сопротивление 0,5 ом. Проводник находится в однородном магнитном поле с индукцией 0,8 тл, линии индукции которого направлены к читателю (рис. 149). Сопротивление всей внешней цепи 2,5 ом. Определить силу тока в проводнике, если он движется перпендикулярно к линиям индукции со скоростью 10 м /сек. Чему равна сила тока в неподвижном проводнике?
Рис. 149. К задаче 35
Э. д. с. индукции Еин = Blv sin α,
F ibl sin альфа что за формула
Если в магнитном поле перемещается проводник таким образом, что он пересекает магнитные силовые линии, то в нем индуктируется э.д.с. Направление этой э.д.с. определяют по правилу правой руки (рис. 5.1): если ладонь правой руки расположить в магнитном поле так, чтобы силовые линии были направлены в ладонь, а большой палец указывал направление перемещения проводника, то остальные четыре вытянутых пальца покажут направление индуктируемой э. д. с.
Значение индуктируемой э. д. с. Е (В) в прямолинейном проводнике пропорционально значению магнитной индукции В (Т), скорости перемещения проводника v (м/c),и активной длине l (м) проводника, которая пересекается магнитными силовыми линиями:
Если проводник пересекает магнитные силовые линии под некоторым углом а (рис. 5.2), то индуктируемая э. д. с.
E = Bvl sin α. (5.2)
Если угол α = 0, то sin α = 0 и э. д. с. Е = 0. В этом случае проводник перемещается вдоль магнитных силовых линий, не пересекая их. Пример. Определить индуктируемую э.д.с. в проводнике длиной 0,5 м, который перемещается со скоростью v = 3 м/с перпендикулярно силовым линиям в однородном магнитном поле, имеющем магнитную индукцию В = 1 Т.
Решение. Индуктируемая в проводнике э.д.с. E = Blv = 1•0,5•3 = 1,5 В.
Когда катушки неподвижны одна относительно другой, а в катушке l изменяют силу тока, например включая и выключая его, то в результате появления и исчезновения магнитного поля, которое воздействует на витки катушки 2, в ней возникает э. д. с.
Если ток в катушке l не меняется, то неизменен и магнитный поток, охватывающий катушку 2, и э. д. с. в ней не индуктируется. Когда к катушке l подведен переменный ток, например промышленной частоты 50 Гц, во второй катушке индуктируется э. д. с, меняющая свое направление с такой же частотой.
В замкнутой электрической цепи с наведенной в ней э. д. с. течет индуктированный ток. Направление этого тока устанавливают по правилу Ленца: индуктированный в проводнике (контуре) ток направлен всегда таким образом, что его магнитное поле противодействует причине, вызвавшей возникновение тока. Иными словами, правило Ленца показывает, что ток, индуктированный в замкнутой цепи, образует свое собственное магнитное поле, направление которого противоположно направлению основного — первичного магнитного поля, породившего этот ток.
Электродвижущая сила, индуктируемая в катушке, с учетом правила Ленца может быть выражена следующей формулой:
где ∆Ф — величина, на которую меняется магнитный поток, охватывающий витки катушки, за отрезок времени At; w — число витков в катушке.
Знак минус в соответствии с правилом Ленца учитывает противодействующее влияние индуктированной э. д. с. Поскольку ток, индуктированный в проводнике (контуре), возникает всякий раз такого направления, при котором он противодействует причине, вызвавшей его, то необходимо прилагать определенное усилие, чтобы перемещать замкнутыйконтур в магнитном, поле. Это усилие можно определить исходя из следующих соображений.Механическая мощность Рм (Вт), необходимая для перемещения со скоростью v (м/с) контура, к которому приложена сила F (Н),
По закону сохранения энергии эта мощность должна быть равнаэлектрической мощности в контуре, в котором индуктируется э. д. с. Еи протекает ток I :
Тогда, подставляя значение E в формулу (5.6), получим:
Основные тригонометрические формулы и тождества sin, cos, tg, ctg
Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Формулы приведения
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.
Формулы приведения являются следствием периодичности тригонометрических функций.
Тригонометрические формулы сложения
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
Тригонометрические формулы сложения
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Формулы кратного угла: двойного, тройного и т.д.
Формулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
Формулы половинного угла
Формулы понижения степени
Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
Общий вид формул понижения степени
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Сумма и разность тригонометрических функций
Произведение тригонометрических функций
Формулы произведения тригонометрических функций
Универсальная тригонометрическая подстановка
Универсальная тригонометрическая подстановка