Доказательство что накрест лежащие углы равны
Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы
Углы и — вертикальные. Очевидно, вертикальные углы равны, то есть
Соответственные углы равны, то есть
Накрест лежащие углы равны, то есть
Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.
Ты нашел то, что искал? Поделись с друзьями!

Периметр параллелограмма — это сумма всех его сторон, то есть

Углы и — односторонние при параллельных прямых и секущей, следовательно,
Теорема о равенстве накрест лежащих углов
Урок 17. Геометрия 7 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Теорема о равенстве накрест лежащих углов»
В формулировке любой теоремы можно выделить две части: условие и заключение. Условие теоремы – это то, что дано, а заключение – это то, что надо доказать.
Например, рассмотрим один из признаков параллельности прямых:
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Здесь условие утверждения: если при пересечении двух прямых секущей накрест лежащие углы равны. А заключение: прямые параллельны.
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
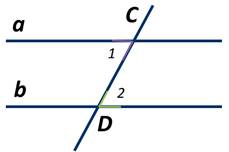
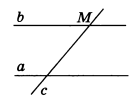
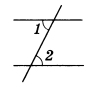
Пусть прямые а и b параллельны и пересечены секущей CD. Доказать, что накрест лежащие углы 1 и 2 равны.
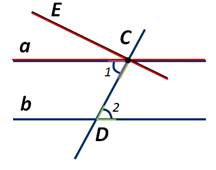
Предположим, что углы 1 и 2 не равны. Тогда от луча CD отложим ∠ЕCD=∠2 так, чтобы ∠ЕCD и ∠2 были накрест лежащими углами при пересечении прямых СЕ и b секущей CD.
По построению эти накрест лежащие углы равны, а поэтому прямая CE параллельна прямой b. Получили, что через точку С проходят две прямые (а и CЕ) параллельные прямой b. А это противоречит аксиоме параллельности прямых. Следовательно, предположение неверно и угол ∠1=∠2. Что и требовалось доказать.
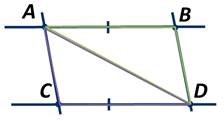
Прямые АВ и CD параллельны. Отрезок АВ=СD. Доказать, что прямая АС параллельна прямой BD.
Рассмотрим треугольник ABD и треугольник ACD.
То есть ∠CAD=∠BDA. А эти углы являются накрест лежащими при прямых AC и BD и секущей AD. Это означает, что прямые AC и BD параллельны. Что и требовалось доказать.
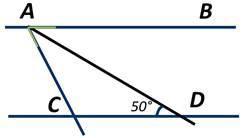
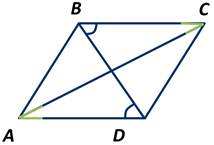
На рисунке ∠CBD=∠ADB. Доказать, что ∠ВСА=∠CAD.
∠ВСА и ∠CAD являются накрест лежащими при параллельных прямых AD и BC и секущей АС, а следовательно, они равны. Что и требовалось доказать.
Отметим, что если доказана какая-либо теорема, то это не означает, что обратная ей теорема верна.
Например, если углы вертикальные, то они равны. А вот если углы равны, то это ещё не означает, что они вертикальные.
Прямая линия. Признаки параллельности прямых линий.
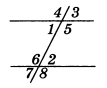
Если две произвольные прямые AB и СD пересечены третьей прямой MN, то образовавшиеся при этом углы получают попарно такие названия:
соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7;
внутренние накрест лежащие углы: 3 и 5, 4 и 6;
внешние накрест лежащие углы: 1 и 7, 2 и 8;
внутренние односторонние углы: 3 и 6, 4 и 5;
внешние односторонние углы: 1 и 8, 2 и 7.
Описанные углы видны на рисунке:
Теорема.
Если две параллельные прямые пересечены третьей прямой, то сформировавшиеся:
1. внутренние накрест лежащие углы одинаковы;
2. внешние накрест лежащие углы одинаковы;
3. соответственные углы одинаковы;
4. сумма внутренних односторонних углов будет 2d = 180 0 ;
5. сумма внешних односторонних углов будет 2d = 180 0 ;
Данную теорему иллюстрирует рисунок:
Имеются две параллельные прямые AB и СD, их пересекает третья прямая MN.
3. ∠ 2 =∠ 6, ∠ 1 = ∠ 5, ∠ 3 = ∠ 7, ∠ 4 = ∠ 8;
4. ∠ 3 + ∠ 6 = 2d и ∠ 4 + ∠ 5 = 2d;
5. ∠ 2 + ∠ 7 = 2d и ∠ 1 + ∠ 8 = 2d.
2. Внешние накрест лежащие углы равны соответственно внутренним накрест лежащим углам, как углы вертикальные.
Так, ∠ 2 = ∠ 4 и ∠ 8 = ∠ 6, но по доказанному ∠ 4 = ∠ 6.
Следовательно, ∠ 2 =∠ 8.
3. Соответственные углы 2 и 6 одинаковы, поскольку ∠ 2 = ∠ 4, а ∠ 4 = ∠ 6. Также убедимся в равенстве других соответственных углов.
5. Сумма внешних односторонних углов будет 2d, потому что эти углы равны соответственно внутренним односторонним углам, как углы вертикальные.
Из выше доказанного обоснования получаем обратные теоремы.
Когда при пересечении двух прямых произвольной третьей прямой получим, что:
1. Внутренние накрест лежащие углы одинаковы;
или 2. Внешние накрест лежащие углы одинаковые;
или 3. Соответственные углы одинаковые;
или 4. Сумма внутренних односторонних углов равна 2d = 180 0 ;
или 5. Сумма внешних односторонних равна 2d = 180 0 ,
Доказательство что накрест лежащие углы равны
Наглядная геометрия 7 класс. Опорный конспект № 3 Параллельные прямые.
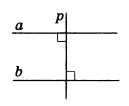
В геометрии нельзя «на глазок» определить, параллельны прямые или нет. Это может быть либо дано, либо доказано. Вы уже знаете, что на плоскости справедлива теорема: «Две прямые, перпендикулярные третьей, параллельны между собой».
Есть еще три признака параллельности прямых, которые можно объединить в одну теорему, она так и называется: «Признаки параллельности прямых». Данные признаки связаны с углами, которые образуются при пересечении двух прямых третьей прямой. Это так называемые накрест лежащие углы, соответственные углы и односторонние углы.
Оказывается, что если накрест лежащие углы равны, или соответственные углы равны, или сумма односторонних углов равна 180°, то прямые будут параллельны.
Справедливы и обратные утверждения. Если даны две заведомо параллельные прямые, которые пересечены третьей, то накрест лежащие углы равны, соответственные углы равны и сумма односторонних углов равна 180°.
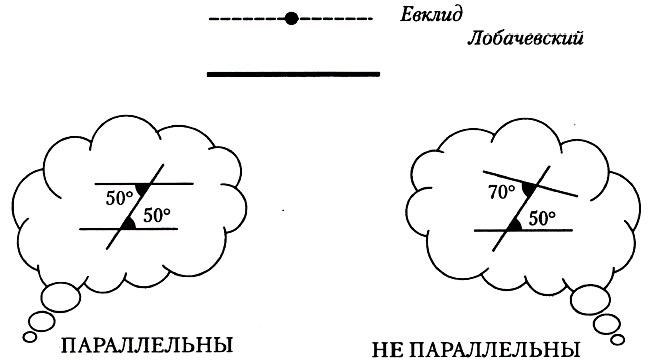
Ранее мы доказали, что через точку вне прямой можно провести единственную прямую, перпендикулярную данной. Можно также доказать, что через точку, не лежащую на прямой, можно провести прямую, параллельную данной. А вот доказать, что такая прямая — единственная, нельзя! Утверждение «Через точку, не лежащую на прямой, можно провести ЕДИНСТВЕННУЮ прямую, параллельную данной» называется аксиомой параллельных прямых. У Евклида эта аксиома называлась пятым постулатом.
На протяжении двух тысячелетий это утверждение вызывало захватывающие и драматичные споры между такими знаменитыми учеными, как Лобачевский, Гаусс и другие. Споры состояли в том, можно или нельзя доказать этот пятый постулат Евклида на основании уже известных теорем. В конце концов работы в этом направлении привели к полному пересмотру научных представлений о геометрии Вселенной.
При пересечении двух прямых третьей, которая называется секущей, образуется 4 пары накрест лежащих углов, 4 пары соответственных и 4 пары односторонних.
3 и 5; 4 и 6 — внутренние накрест лежащие углы;
1 и 7; 2 и 8 — внешние накрест лежащие углы;
1 и 5; 2 и 6; 4 и 8; 3 и 7 — соответственные углы;
3 и 6; 4 и 5 — внутренние односторонние углы;
2 и 7; 1 и 8 — внешние односторонние углы.
Признаки параллельности прямых. Если накрест лежащие углы равны, ши соответственные углы равны, ши сумма односторонних углов равна 180°, то прямые параллельны. В первую очередь нужно доказать, что если накрест лежащие углы равны, то прямые параллельны. Доказательство опирается на уже доказанное нами свойство: две прямые, перпендикулярные третьей, параллельны между собой. Из середины отрезка секущей опускают перпендикуляр на одну из параллельных прямых. Затем перпендикуляр продляют до пересечения со второй прямой. Из равенства полученных треугольников следует, что прямая, проходящая через перпендикуляр, будет перпендикулярна и второй прямой. Дальнейшее просто.
Через точку, не лежащую на данной прямой, МОЖНО провести прямую, параллельную данной. Опустив перпендикуляр из точки на прямую, а затем, восставив перпендикуляр к проведенной прямой, получим две прямые, перпендикулярные третьей, которые будут параллельны. А вот доказать, что такая прямая единственная, нельзя. Поэтому справедлива АКСИОМА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ: «Через точку, не лежащую на данной прямой, проходит ЕДИНСТВЕННАЯ прямая, параллельная данной».
Теорема о двух прямых, параллельных третьей. Две прямые, параллельные третьей, параллельны между собой. Если бы они пересекались, то через одну точку проходили бы две прямые, параллельные третьей.
Теорема о пересечении параллельных прямых. Если на плоскости прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. Если бы эта прямая не пересекала вторую прямую, то она была бы ей параллельна. Но тогда через одну точку проходили бы две прямые, параллельные третьей. А это невозможно.
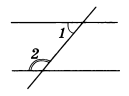
Свойства углов при параллельных прямых и секущей. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны, соответственные углы равны и сумма односторонних углов равна 180°. В первую очередь нужно доказать, что если прямые параллельны, то накрест лежащие углы равны. Пусть прямые параллельны, а накрест лежащие углы 1 и 2 не равны. Отложим угол, равный углу 2, как показано на рисунке. Получим еще одну прямую, параллельную нижней прямой (если накрест лежащие углы равны, то прямые параллельны). Но через точку нельзя провести две прямые, параллельные третьей. Значит, наше предположение неверно, и накрест лежащие углы равны. Остальное несложно.
Из указанных свойств параллельных прямых вытекает важное следствие: перпендикуляр к одной из параллельных прямых будет перпендикуляром и к другой. Доказательство следует из равенства соответственных углов.
Теорема об углах с соответственно параллельными сторонами. Углы с соответственно параллельными сторонами равны, если они одновременно острые ши одновременно тупые, и в сумме составляют 180°, если один из них острый, а другой — тупой. Продлив стороны данных углов, получим две пары равных соответственных углов, откуда ∠1 = ∠2. Продлив сторону угла 1 за его вершину, получим доказательство второй части теоремы.
Теорема об углах с соответственно перпендикулярными сторонами. Углы с соответственно перпендикулярными сторонами равны, если они одновременно острые или одновременно тупые, и в сумме составляют 180°, если один из них острый, а другой — тупой. Проведя перпендикулярные лучи из вершины угла 1, получим, что углы 2 и 3 равны и углы 3 и 1 дополняют один и тот же угол 4 до 90°. Значит, ∠1 = ∠3, ∠1 = ∠2. Продлив сторону угла 2 за его вершину, получим доказательство второй части теоремы.
Это опорный конспект № 3 по геометрии в 7 классе «Параллельные прямые (опорный конспект)». Выберите дальнейшие действия:
Инструменты пользователя
Инструменты сайта
Боковая панель
Геометрия:
Контакты
Признаки параллельности двух прямых. Свойства параллельных прямых
Признаки параллельности двух прямых
Теорема 1. Если при пересечении двух прямых секущей:
прямые параллельны (рис.1).
Доказательство. Ограничимся доказательством случая 1.
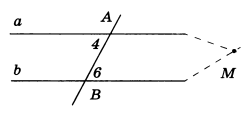
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 4 = ∠ 6. Докажем, что а || b.
Предположим, что прямые а и b не параллельны. Тогда они пересекаются в некоторой точке М и, следовательно, один из углов 4 или 6 будет внешним углом треугольника АВМ. Пусть для определенности ∠ 4 — внешний угол треугольника АВМ, а ∠ 6 — внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 4 больше ∠ 6, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.
Замечание. Способ, которым мы только что доказали случай 1 теоремы 1, называется методом доказательства от противного или приведением к нелепости. Первое название этот способ получил потому, что в начале рассуждения делается предположение, противное (противоположное) тому, что требуется доказать. Приведением к нелепости он называется вследствие того, что, рассуждая на основании сделанного предположения, мы приходим к нелепому выводу (к абсурду). Получение такого вывода заставляет нас отвергнуть сделанное вначале допущение и принять то, которое требовалось доказать.
Задача 1. Построить прямую, проходящую через данную точку М и параллельную данной прямой а, не проходящей через точку М.
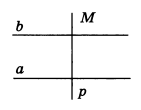
Решение. Проводим через точку М прямую р перпендикулярно прямой а (рис. 3).
Затем проводим через точку М прямую b перпендикулярно прямой р. Прямая b параллельна прямой а согласно следствию из теоремы 1.
Из рассмотренной задачи следует важный вывод:
через точку, не лежащую на данной прямой, всегда можно провести прямую, параллельную данной.
Основное свойство параллельных прямых состоит в следующем.
Аксиома параллельных прямых. Через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.
1) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую (рис.4).
2) Если две различные прямые параллельны третьей прямой, то они параллельны (рис.5).
Справедлива и следующая теорема.
Теорема 2. Если две параллельные прямые пересечены секущей, то:
Следствие 2. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой (см. рис.2).
Замечание. Теорема 2 называется обратной теореме 1. Заключение теоремы 1 является условием теоремы 2. А условие теоремы 1 является заключением теоремы 2. Не всякая теорема имеет обратную, т. е. если данная теорема верна, то обратная теорема может быть неверна.
Поясним это на примере теоремы о вертикальных углах. Эту теорему можно сформулировать так: если два угла вертикальные, то они равны. Обратная ей теорема была бы такой: если два угла равны, то они вертикальные. А это, конечно, неверно. Два равных угла вовсе не обязаны быть вертикальными.
Пример 1. Две параллельные прямые пересечены третьей. Известно, что разность двух внутренних односторонних углов равна 30°. Найти эти углы.
Решение. Пусть условию отвечает рисунок 6.
Углы 1 и 2 внутренние односторонние, их сумма равна 180°, т. е.
∠ l + ∠ 2 = 180°. (1)
Подставим в равенство (1) значения углов 1 и 2, получим
х + 30° + х = 180°.
Пример 2. Две параллельные прямые пересечены третьей. Известно, что сумма двух внутренних накрест лежащих углов равна 150°. Чему равны эти углы и остальные шесть?
Решение. Пусть условию задачи соответствует рисунок 7.
Углы 1 и 2 внутренние накрест лежащие, следовательно, они равны. Сумма этих углов по условию задачи равна 150°, тогда ∠ 1 = ∠ 2 = 75°.
Найдем остальные углы (рис. 8):
Получили четыре угла по 75°, четыре угла по 105°.