Доказательство что среднее арифметическое больше среднего геометрического

Различные средние положительных. Неравенство Коши

Главная > Документ

Соотношение между средними величинами.

Сравнение среднего арифметического и среднего геометрического.

Применим формулу «квадрат разности»:

Прибавим к обеим частям неравенства 4ав :

Применим формулу «квадрат суммы»:

Разделим обе части неравенства на 4 :

;

Так как а и в – положительные по условию, то извлечём из обеих частей неравенства квадратный корень:

Получили искомое выражение.

Сравнение среднего арифметического и среднего квадратичного.

Для доказательства рассмотрим разность

Сравнение среднего гармонического и среднего геометрического.

Докажем, что среднее гармоническое не больше среднего геометрического, то есть . Рассмотрим разность

Таким образом мы доказали одно из важнейших неравенств, связанных со средними:

.

Дано: окр. (О;ОА); AD = a ; BD = b

Доказать:

АВ – диаметр, АВ = a + b и , следовательно, .

угол АСВ – вписанный

дуга АКВ = 180° значит, угол АСВ = 90 ° (по свойству вписанного угла)

Таким образом, ∆АСВ – прямоугольный,

(по общему острому углу)

2) ∆АВС подобен ∆ CBD

4) , следовательно,

, следовательно,

, следовательно, , значит, , то есть .

Поэтому , что и требовалось доказать.

Это неравенство можно доказать и другим способом.

Дано: ABCD – прямоугольный, AD = a, AB = b, AK – биссектриса угла ВАD.

Доказать:

АК – биссектриса, следовательно, ВАL = LAD. LAD и BLA – внутренние накрест лежащие углы при параллельных ВС и AD и секущей AL, то есть BLA = LAD.

В = 90°, следовательно, BAL = LAD = 45°, но BLA = LAD, значит, ∆ АВL – равнобедренный, BL = AB = b.

∆ AKD – равнобедренный, так как KD ┴ AD, DAL = 45°, значит AD = KD = a.

4)

Очевидно, что , равенство достигается при

; ,

или ,

то есть среднее геометрическое не больше среднего арифметического.

Сравнение среднего квадратичного и среднего арифметического.

Средние величины можно находить для любого количества положительных чисел . Определения этих средних даны выше. Для любых положительных чисел среднее арифметическое, среднее геометрическое, среднее гармоническое, среднее квадратичное удовлетворят неравенствам:

,

в каждом из которых знак равенства достигается лишь в случае, когда .

Самым важным и значимым из этих неравенств является неравенство о среднем арифметическом и среднем геометрическом, которое носит название неравенства Коши.

Замечательные пределы, порождаемые классическими средними.

Например, взяв среднее геометрическое и среднее арифметическое и отправляясь от чисел 1 и 3, получаем

В этом примере последовательности и очень быстро сближаются. Всегда ли так будет? Оказывается, подобные последовательности всегда имеют общий предел.

Арифметико – гармоническое среднее.

Пусть выбранная пара средних – это среднее гармоническое и среднее арифметическое; таким образом, члены последовательностей и определяются формулами

, , , .

Рассмотрим среднее гармоническое, среднее геометрическое и среднее арифметическое

.

Отсюда следует, что

.

То есть последовательность возрастает «навстречу» убывающей последовательности .

Таким образом, обе последовательности монотонны и ограничены, следовательно, они имеют пределы. Пусть , . Вычислим предел

Так как и , где n =0, 1, 2, 3,… ; ; , то

, поэтому

Поэтому .

Арифметико – гармоническое среднее совпадает со средним геометрическим.

; .

и далее все знаки стабилизируются:

.

Арифметико – геометрическое среднее.

Четырнадцатилетний карл Фридрих Гаусс обнаружил на числовых примерах, что при вычислении последовательностей и с помощью арифметических и геометрических средних:

, ,

эти последовательности очень быстро сближаются.

Их общий предел называется арифметико – геометрическим средним чисел a и b и обозначается через . Найти явное выражение через a и b очень не просто. Впервые оно было получено Гауссом в результате необычайно остроумных и виртуозных рассуждений и преобразований, использующих свойства так называемых эллиптических интегралов.

Геометрическо – гармоническое среднее.

Если строить последовательности и с помощью средних гармонических и средних геометрических:

; ,

то в этом случае они сходятся к общему пределу. Назовём его геометрическо – гармоническим средним a и b и обозначим его через . Однако ничего существенно нового по сравнению с предыдущими последовательностями здесь нет, так как

; .

.

Источник

Неравенство о среднем арифметическом и среднем геометрическом

Неравенство о среднем арифметическом и среднем геометрическом (неравенство Коши)

Среднее арифметическое n положительных чисел не меньше их среднего геометрического:

причём равенство достигается тогда и только тогда, когда

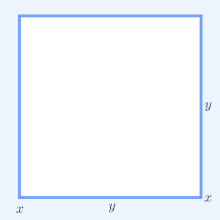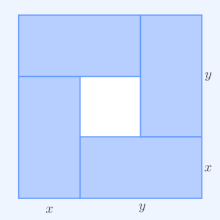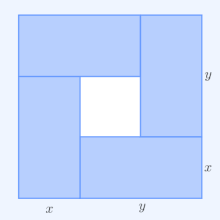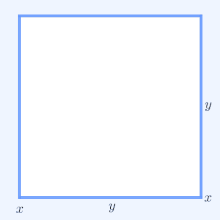
Частный случай этого неравенства, связывающий среднее арифметическое и среднее геометрическое двух положительных чисел, известен с древних времён. Чаще всего его доказывают, используя геометрическую интерпретацию.

Пусть AD=a, BD=b.

Построим окружность с диаметром AB=a+b.

Из произвольной точки C окружности проведём к диаметру перпендикуляр CD.

По свойству прямоугольного треугольника, высота, проведённая к гипотенузе, равна среднему геометрическому между проекциями катетов на гипотенузу:

Соединим точку C с центром окружности, точкой O. CO — радиус, значит, он равен половине диаметра:

то есть длина CO равна среднему арифметическому a и b.

В прямоугольном треугольнике COD CD — катет, CO — гипотенуза.

Так как гипотенуза всегда больше катета, CO>CD, следовательно, среднее арифметическое a и b больше их среднего геометрического.

D совпадает с точкой O,

если AO=BO, то есть a=b.

(так как a>0), и и ф этом случае среднее арифметическое a и b равно их среднему геометрическому.

Таким образом, среднее арифметическое положительных чисел a и b не меньше их среднего геометрического.

В общем случае неравенство было доказано Коши.

Источник

Среднее геометрическое против среднего арифметического

Разница между средним геометрическим и средним арифметическим

Среднее арифметическое и среднее геометрическое являются инструментами, широко используемыми для расчета доходности инвестиций для инвестиционных портфелей в мире финансов. Люди используют среднее арифметическое, чтобы сообщать о более высокой прибыли, которая не является правильной мерой расчета прибыли на инвестиции. Поскольку окупаемость инвестиций в портфель по годам зависит от доходности в предыдущие годы, среднее геометрическое является правильным способом расчета окупаемости инвестиций за определенный период времени. Среднее арифметическое лучше подходит в ситуации, когда переменные, используемые для расчета среднего значения, не зависят друг от друга.

Пример: использование пригодности среднего геометрического и среднего арифметического

Что создает неправильное впечатление, что инвестор безубыточен на своих инвестициях и нет никаких потерь или прибыли. Однако более тщательный анализ дает совершенно иную картину сценария.

Среднее геометрическое возвращений

Это означает, что годовая доходность портфеля была отрицательной 13, 40%. Инвестиционная позиция после двух лет выглядит следующим образом:

2. Когда нужно вычислить среднее значение переменных, которые не зависят друг от друга, арифметика означает подходящий инструмент для вычисления среднего. Среднее количество баллов студента по 5 предметам может быть рассчитано по среднему арифметическому, так как баллы студента по различным предметам не зависят друг от друга.

Сравнение геометрического среднего с средним арифметическим (инфографика)

Ниже приведена верхняя 8 разница между средним геометрическим и средним арифметическим

Ключевые различия между средним геометрическим и средним арифметическим

Давайте обсудим некоторые основные различия между средним геометрическим и средним арифметическим:

Среднее геометрическое и среднее арифметическое Сравнительная таблица

Давайте посмотрим на 8 лучших Сравнение среднего геометрического и среднего арифметического

Среднее арифметическое

Среднее геометрическое

Среднее геометрическое и среднее арифметическое находят свое применение в экономике, финансах, статистике и т. Д. В зависимости от их пригодности. Среднее геометрическое больше подходит для расчета среднего и дает точные результаты, когда переменные являются зависимыми и широко искажены. Тем не менее, среднее арифметическое значение используется для расчета среднего значения, когда переменные не являются взаимозависимыми. Поэтому, эти два должны использоваться в соответствующем контексте, чтобы получить лучшие результаты.

Рекомендуемые статьи

Это было руководством к разнице между средним геометрическим и средним арифметическим. Здесь мы также обсудим ключевые различия между средним геометрическим и арифметическим средними значениями с помощью инфографики и сравнительной таблицы. Вы также можете взглянуть на следующие статьи, чтобы узнать больше.

Источник

Доказательство что среднее арифметическое больше среднего геометрического

Зачастую в средних класах мы пользуемся известным выражением о том, что среднее арифметическое двух неотрицательных чисел больше чем среднее геометрические их значение:

Доказывается неравенство достаточно просто. Умнажаем обе части на 2 и переносим правую честь влево:

Что и требовалось доказать.

Для двух положительных чисел оно имеет следующий вид (общий случай для n чисел):

Пусть a, b ∈ R, тогда иммет место неравенство:

Докажем его. Покажем, что среднее геометрическое больше, чем среднее гармоническое.

Что и требовалось доказать.

Соотношение между средним арифметическим и средним геометрическим рассматривалось выше. Докажем, что среднее квадратическое больше среднего арифметического:

√ (a 2 + b 2 ) / 2 ≥ (a + b) / 2; так как справа положительное число, подносим в квадрат обе части:

(a 2 + b 2 ) / 2 ≥ (a 2 + 2ab + b 2 ) / 4; переносим все в левую часть, умножаем на 4:

Что и требовалось доказать.

Неравенство имеет место для n чисел и звучит так:

На данный момент в базе присутствует информация о 1847 великих математиках.

Для ознакомления доступны 48 книг.

Добавлен материал «Показательные уравнения и неравенства», в котором заполнены разделы «Теория» и «Методы решений». В ближайшее время ожидайте задачи по этому материалу.

Источник

СОДЕРЖАНИЕ

Среднее геометрическое аналогично, за исключением того, что она определена только для списка неотрицательных действительных чисел, и использует умножение и корень вместо сложения и деления:

Неравенство

Геометрическая интерпретация

его можно пересчитать, умножив на n 2 n –1, чтобы получить

Пример приложения

Кроме того, мы знаем, что две стороны равны именно тогда, когда все члены среднего равны:

Практическое применение

Доказательства неравенства AM – GM.

Доказательство с использованием неравенства Дженсена

Неравенство Дженсена утверждает, что значение вогнутой функции среднего арифметического больше или равно среднему арифметическому значений функции. Поскольку функция логарифмирования вогнутая, имеем

Взяв антилогари крайних левых и крайних правых частей, мы получаем неравенство AM – GM.

Доказательство усреднением среднего арифметического.

Мы должны показать, что

Таким образом, правая часть будет наибольшей, когда все x _i s равны среднему арифметическому.

таким образом, поскольку это наибольшее значение правой части выражения, мы имеем

В общем случае вышеупомянутый процесс усреднения действительно стремится к равным числам, и это доказывает AM-GM.

знак равно 2 ( d я 2 + d j 2 ) 2 <\ displaystyle = 2 \ left (<\ frac > <2>> + <\ frac > <2>> \ right) ^ <2>>

Доказательства индукции

Доказательство по индукции # 1.

Для следующего доказательства мы применяем математическую индукцию и только хорошо известные правила арифметики.

Базис индукции: для n = 1 утверждение верно с равенством.

Гипотеза индукции. Предположим, что утверждение AM – GM выполняется для любого выбора n неотрицательных действительных чисел.

Теперь определим y с помощью

Благодаря (*) мы знаем, что

что завершает доказательство.

Доказательство по индукции # 2.

Прежде всего докажем, что для действительных чисел x ₁ и x ₂ > 1 следует

откуда сразу получается требуемое неравенство.

Базис индукции: для n = 2 утверждение верно в силу указанного выше свойства.

Однако с учетом базиса индукции имеем

что завершает доказательство.

Доказательство Коши с использованием индукции вперед – назад.

Случай, когда все члены равны

Если все условия равны:

Случай, когда не все члены равны

Этот случай значительно сложнее, и мы разбиваем его на подслучаи.

Подслучай, когда n = 2

Подслучай, когда n = 2 k

где в первом неравенстве две стороны равны, только если

(в этом случае первое среднее арифметическое и первое среднее геометрическое равны x ₁ и аналогично второму среднему и второму среднему геометрическому); а во втором неравенстве две стороны равны, только если два средних геометрических равны. Поскольку не все 2 k числа равны, невозможно, чтобы оба неравенства были равенствами, поэтому мы знаем, что:

Подслучай, когда n k

Итак, если у нас есть n терминов, то давайте обозначим их среднее арифметическое через α и расширим наш список терминов следующим образом:

α ≥ Икс 1 Икс 2 ⋯ Икс п п <\ displaystyle \ alpha \ geq <\ sqrt [] x_ <2>\ cdots x_ >>>

Доказательство по индукции с использованием основного исчисления.

Базис индукции : для n = 1 утверждение верно с равенством.

с равенством, только если все числа n + 1 равны.

Если все числа равны нулю, неравенство выполняется с равенством. Если некоторые, но не все числа равны нулю, мы имеем строгое неравенство. Поэтому в дальнейшем мы можем считать, что все n + 1 числа положительны.

Рассмотрим последнее число x _{n +1} как переменную и определим функцию

Первая производная от f дается формулой

После небольшой переделки получаем

Доказательство Полиа с использованием экспоненциальной функции

Доказательство с помощью лагранжевых множителей.

Обобщения

Весовое неравенство AM – GM.

Доказательство с использованием неравенства Дженсена

Поскольку x _k с весом w _k = 0 не влияет на неравенство, в дальнейшем мы можем предполагать, что все веса положительны. Если все x _k равны, то равенство выполняется. Поэтому остается доказать строгое неравенство, если не все они равны, что мы и будем предполагать в дальнейшем. Если хотя бы один x _k равен нулю (но не все), то средневзвешенное геометрическое среднее равно нулю, а средневзвешенное арифметическое положительно, следовательно, выполняется строгое неравенство. Следовательно, мы можем также считать, что все x _k положительны.

Матричное арифметическое среднее геометрическое неравенство

Позже те же авторы доказали более сильное неравенство, что

Это предполагаемое неравенство было показано Стивеном Друри в 2012 году.

SW Друри, По вопросу о Бхатиа и Киттане, Linear Algebra Appl. 437 (2012) 1955–1960.

Другие обобщения

Другие обобщения неравенства средних арифметических и геометрических включают:

Источник