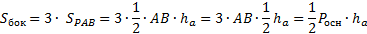Докажите что боковая поверхность правильной пирамиды равна произведению полупериметра на основание
Теорема о площади боковой поверхности правильной пирамиды



Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему:
Для доказательства выберем правильную треугольную пирамиду.
Дано: РАВС – правильная треугольная пирамида.
Доказать: 
РАВС – правильная треугольная пирамида. То есть АВ = АС = ВС. Пусть О – центр треугольника АВС, тогда РО – это высота пирамиды. В основании пирамиды лежит равносторонний треугольник АВС. Заметим, что 
Треугольники РАВ, РВC, РСА – равные равнобедренные треугольники (по свойству). У треугольной пирамиды три боковые грани: РАВ, РВC, РСА. Значит, площадь боковой поверхности пирамиды равна:
Задача 1
Радиус окружности, вписанной в основание правильной четырехугольной пирамиды, равен 3 м, высота пирамиды равна 4 м. Найдите площадь боковой поверхности пирамиды.
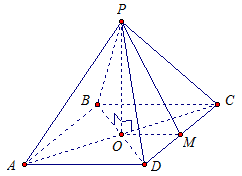
Дано: правильная четырехугольная пирамида АВСD,
РО – высота пирамиды,
По доказанной теореме, 
Найдем сначала сторону основания АВ. Нам известно, что радиус окружности, вписанной в основание правильной четырехугольной пирамиды, равен 3 м.
Тогда, 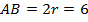
Найдем периметр квадрата АВСD со стороной 6 м:
Рассмотрим треугольник BCD. Пусть М – середина стороны DC. Так как О – середина BD, то 
Треугольник DPC – равнобедренный. М – середина DC. То есть, РМ – медиана, а значит, и высота в треугольнике DPC. Тогда РМ – апофема пирамиды.
РО – высота пирамиды. Тогда, прямая РО перпендикулярна плоскости АВС, а значит, и прямой ОМ, лежащей в ней. Найдем апофему РМ из прямоугольного треугольника РОМ.

Теперь можем найти боковую поверхность пирамиды:
ЭСО «МНОГОГРАННИКИ»
Правильная пирамида
О высоте правильной пирамиды
В правильной пирамиде отрезок, соединяющий вершину пирамиды с центром её основания, является высотой пирамиды.
Для определённости проведём доказательство для правильной шестиугольной пирамиды SABCDEF:
Таким образом, прямая SO перпендикулярна двум пересекающимся прямым FC и AD плоскости основания, а значит она перпендикулярная этой плоскости. Таким образом отрезок SO перпендикулярен плоскости основания, т.е. является высотой пирамиды.
В случае правильной пирамиды, основанием которой служит n-угольник с чётным числом вершин, доказательство аналогично. В случае, когда основанием пирамиды служит многоугольник с нечётным числом вершин, для доказательства можно воспользоваться тем, что основание высоты правильной пирамиды совпадает с центром окружности, описанной около его основания.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
Доказательство проведём для правильной шестиугольной пирамиды TABCDEF:
Площадь боковой поверхности равна сумме указанных равнобедренных треугольников, т.е.:
Sбок = ½ ABℓ + ½ BCℓ + ½ CDℓ + ½ DEℓ + ½ EFℓ + ½ FAℓ = ½ ℓ(AB + BC + CD + DE + EF + FA) = ½ Pоснℓ.
Геометрия. 10 класс
Пирамида
Пирамида
Необходимо запомнить
На этом уроке мы ввели понятие пирамиды. Пирамидой будем называть многогранник, составленный из n-угольника и n треугольников, при этом n-угольник называется основанием пирамиды, а треугольники – боковыми гранями. Высотой пирамиды будем называть перпендикуляр, проведенный из вершины пирамиды к плоскости основания. Высота может лежать как внутри пирамиды, так вне ее, в боковой грани или являться ребром.
Название пирамиды зависит от многоугольника, лежащего в основании. Например, пирамида, в основании которой лежит четырехугольник, называется четырехугольной.
Среди пирамид выделяют правильные пирамиды, прямоугольные и усеченные пирамиды.
Также на уроке мы доказали некоторые свойства пирамид, и вывели формулу для вычисления площади боковой поверхности правильной пирамиды.
Пирамида
Пирамиды – одна из загадок человечества. По всему миру было возведено множество пирамид: пирамиды были найдены в Египте, Индии, Мексике и в других странах.
В основном эти постройки выполняли роль храма или усыпальницы. Но почему они имеют именно такую форму? На этот счет ведется много споров, по некоторым из предположений, пирамида – простое в строительстве сооружение, которое отличается от обычных домов, имеющих форму прямоугольного параллелепипеда. Другие утверждают, что пирамида символизирует устремление к солнцу и свету.
Одни из наиболее известных и величественных – пирамиды в Египте.
Размеры пирамиды Хеопса удивляют даже современного человека. Ее основание занимает огромную площадь в 53 тыс. квадратных метров, что соразмерно десяти футбольным полям. Не менее поражают и другие параметры: длина основания – 230 м, длина бокового ребра – столько же, а площадь боковой поверхности – 85,5 тыс. квадратных метров.
Сейчас высота пирамиды Хеопса равна 138 метрам, однако изначально она достигала 147 метров, что можно сравнить с пятидесятиэтажным небоскребом.
На строительство пирамиды пошло около 2 300 000 каменных блоков, объемом свыше 1 м3 каждый.
В настоящее время, чтобы перевезти все камни, из которых сложена пирамида Хеопса понадобится 20 тысяч товарных поездов по 30 вагонов в каждом!
Для площади боковой поверхности усеченной пирамиды верна следующая теорема.
Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.
Площадь боковой поверхности – сумма площадей боковых граней, то есть сумма площадей трапеций. Площадь трапеции вычисляется как произведение полусуммы оснований на высоту. Поскольку трапеции равны, то и длину апофемы d можно вынести за скобки. В скобках останется сумма длин сторон верхнего и нижнего оснований. То есть периметры верхнего и нижнего оснований.
Что и требовалось доказать.
Формула для вычисления площади боковой поверхности усеченной пирамиды будет выглядеть следующим образом:
Видеоурок «Правильная Пирамида»
§ 1 Понятие правильной пирамиды
На этом уроке мы с вами рассмотрим понятие правильной пирамиды, и докажем теорему о площади боковой поверхности правильной пирамиды.
Пирамиды, которые чаще всего мы видим это правильные пирамиды, а называются они так потому, что в основании у них лежит правильный многоугольник. Например, равносторонний треугольник, квадрат, правильный шестиугольник, или вообще любой другой правильный n-угольник. Например, известные всем египетские пирамиды – это правильные четырехугольные пирамиды. Интересный факт, стороны основания пирамиды Хеопса, являющегося почти квадратом, составляют около 230 метров, ну а если вычислить площадь основания, то она будет приблизительно равна 5,3 гектара, что в два раза больше Красной площади в Москве.
Начнем изучение правильной пирамиды с определения. Пирамида называется правильной, если ее основанием служит правильный многоугольник, а отрезок соединяющий вершину пирамиды с центром основания, является ее высотой. Напомним, что центром правильного многоугольника называется центр вписанной в него окружности.
§ 2 Теорема о площади боковой поверхности правильной пирамиды
Надо отметить, что все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками. Докажем это. Рассмотрим правильную пирамиду PА1А2А3…Аn. Сначала докажем, что все боковые ребра равны. Любое боковое ребро представляет собой гипотенузу прямоугольного треугольника, одним катетом которого служит высота РО пирамиды, а другим — радиус описанной около основания окружности (например, боковое ребро РА1 – гипотенуза треугольника ОРА1, в котором ОР=h, ОА1=R). По теореме Пифагора любое боковое ребро равно корню квадратному из суммы квадрата высоты и квадрата радиуса описанной окружности. Поэтому РА1=РА2=…РАn.
Мы доказали что боковые ребра правильной пирамиды равны из этого можно сделать вывод, что боковые грани — равнобедренные треугольники. Если добавить что у каждого из этих треугольников основанием является сторона правильного многоугольника, то боковые грани – это равные равнобедренные треугольники. А вывод этот сделан на основании признака равенства треугольников по трем сторонам.
Введем новое определение. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. На рисунке РЕ апофема. Так как мы уже выяснили, что все боковые грани равные равнобедренные треугольники, то можно с уверенность говорить, что все апофемы правильной пирамиды равны друг другу.
Боковые грани правильной пирамиды – равные равнобедренные треугольники, основания которых – стороны основания пирамиды, а высоты равны апофеме. Площадь S боковой поверхности пирамиды равна сумме произведений сторон основания на половину апофемы d. Вынося множитель ½ d за скобки, получим в скобках сумму сторон основания пирамиды, т.е. периметр. Получилось, что площадь боковой поверхности правильной пирамиды равна ½ произведения периметра основания на апофему. Нами была доказана теорема о площади боковой поверхности правильной пирамиды. Дадим ей формулировку. Площадь боковой поверхности правильной пирамиды равна произведению полупериметра основания на высоту боковой грани.
§ 3 Интересные факты
В свое время были измерены всевозможные параметры пирамид Древнего Египта, в том числе и пирамиды, о которой шла речь на этом уроке – пирамиды Хеопса, самого древнего чуда света, единственного сохранившегося до наших дней. Ученые, измерившие эти величины, вычислили, что площадь боковой поверхности пирамиды составляет 85500м².
Мы рассмотрели на этом уроке понятие правильной пирамиды и дали ей точное определение. Разобрали, что все боковые ребра правильной пирамиды являются равными отрезками, а все боковые грани равные равнобедренные треугольники. Доказали теорему о площади боковой поверхности правильной пирамиды.
Презентация по математике «Пирамида»
Описание презентации по отдельным слайдам:
Учитель математики МОУ Кузнечихинская СШ ЯМР Увава Е.А.
Цель урока: Изучить новый вид многогранников – пирамида Выйти на понятие правильной пирамиды, усечённой пирамиды Изучить свойства пирамиды
(А1В1С1) || (АВС) Пирамида SАВС подобна пирамиде SА1В1С1
Сечение пирамиды плоскостью, проходящей через вершину и диагональ основания, называется диагональным сечением. Сечения пирамиды плоскостями, проходящими через её вершину, представляют собой треугольники.
Если пирамиду пересечь плоскостью, параллельной плоскости основания, то: б) в сечении образуется многоугольник, подобный основанию пирамиды; (О1А1В1С1 подобен ОАВС)
A B C S SABC – тетраэдр 3.Чему равна площадь поверхности правильного тетраэдра с ребром 1? Решение 1. Sпов=4Sтр 2. Sтр = 0,5а2sin600 Ответ: 3. Sпов=4 • 0,5а2sin600 = =
Домашнее задание 1). Если в правильной треугольной пирамиде высота H равна стороне основания a, то боковые ребра составляют с плоскостью основания углы в 600. Верно ли это утверждение? 2). Сторона квадрата равна 10 см. Доказать, что нельзя, используя его в качестве основания, построить правильную четырехугольную пирамиду с боковым ребром 7 см. 3). Доказать или опровергнуть утверждение: «если в пирамиде все ребра равны, то пирамида правильная».
Постройте сечение пирамиды, плоскостью, проходящей через заданные точки. М N K A B C D S Домашнее задание
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДA-035237
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Путин поручил разработать концепцию развития допобразования детей до 2030 года
Время чтения: 2 минуты
В России будут создавать школьные театры
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
В школах Тюмени запустят раздельный сбор отходов
Время чтения: 1 минута
В Ленобласти педагоги призеров и победителей олимпиады получат денежные поощрения
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.