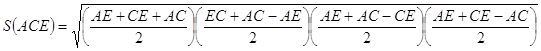Докажите что через две скрещивающиеся прямые можно провести параллельные плоскости

Докажите, что через две скрещивающиеся прямые можно провести параллельные плоскости (рис. 36)

2.14. Докажите, что через две скрещивающиеся прямые можно провести параллельные плоскости (рис. 36).

Решение: Пусть прямые а и b скрещиваются. Выберем на прямой а произвольно точку А и проведем прямую с, параллельную b (через точку, не лежащую на данной прямой можно провести единственную прямую, параллельную данной). Прямые а и с задают плоскость β. По признаку параллельности прямой и плоскости: b || β. Аналогично, проведем прямую d в плоскости α.

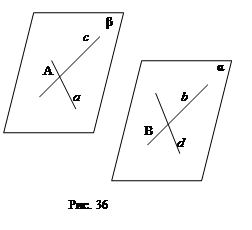
α || β (если две пересекающиеся прямые плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны).

3.06. Постройте сечение пятиугольной пирамиды PABCDE плоскостью α, которая проходит через внутреннюю точку М основания ABCDE параллельно грани РAB (рис. 37).

Решение: Так как прямые, по которым две параллельные плоскости пересечены третьей плоскостью, параллельны, а плоскость α параллельна грани РАВ, то: а) прямая пересечения плоскости α с плоскостью основания пирамиды должна быть параллельна АВ; б) прямая пересечения α с плоскостью грани РВС – параллельна АР; в) прямая пересечения α с плоскостью РАD – параллельна РА, поэтому проводим: 1) через точку М прямую KF || AB; 2) FH || PA; 3) KR || PB; 4) ML || AP. Пятиугольник HLRKF – искомое сечение. В доказательстве используется признак параллельности прямой и плоскости, признак параллельности плоскостей.

3.07. Точки А, В и С лежат в плоскости α и не лежат на одной прямой. Равные и параллельные отрезки АА₁, ВВ₁ и СС₁ расположены по одну сторону от плоскости α. Докажите, что (А₁В₁С₁) || 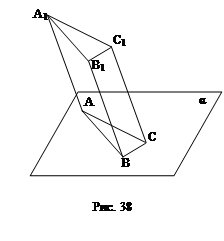(АВС) (рис. 38).

Решение: ВВ₁С₁С – параллелограмм (из параллельности и равенства ВВ₁ и СС₁), следовательно ВС || В₁С₁. АВ || А₁В₁ (аналогично). По теореме о параллельности плоскостей (по двум пересекающимся прямым): (А₁В₁С₁) || (АВС).

Решение: а)Заметим, что ΔAEC и не лежащая в нем точка В образуют тетраэдр ВАСЕ. МК || АС (МК – средняя линия ΔAВC). КР || СЕ (КР – средняя линия ΔВCЕ). По теореме о параллельности плоскостей (через пересекающиеся прямые): (МКР)||(АСЕ).

б) По формуле Герона:

, как средние линии соответствующих треугольников. Подставим данные значения в формулу: . Отсюда .

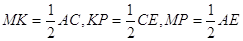
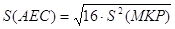
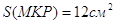
3.09. Три отрезка А₁А₂, В₁В₂ и С₁С₂, не лежащие в одной плоскости, имеют общую середину. Докажите, что плоскости А₁В₁С₁ и А₂В₂С₂ параллельны (рис. 40).

Решение: Каждые две пересекающиеся прямые задают плоскость (через любые две пересекающиеся прямые можно провести плоскость, и притом только одну). Так как точка пересечения делит прямые пополам, то по теореме Фалеса: А₁В₁ || В₂А₂. Аналогично доказывается параллельность С₁В₁ и С₂В₂, А₁В₁ и А₂В₂. По теореме о параллельности плоскостей (через пересекающиеся прямые): (А₁В₁С₁)||(А₂В₂С₂).

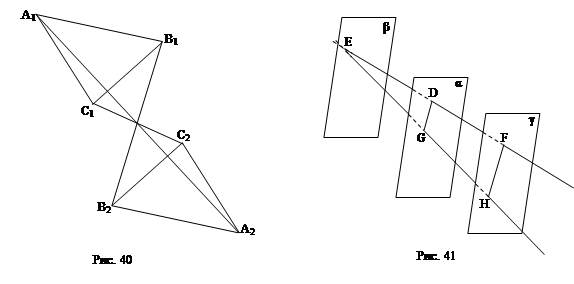
3.10. Прямая DF пересекает параллельные плоскости α, β и γ соответственно в точках D, Е и F, при этом DF = 3, ЕF = 9 (рис. 41). Прямая EG пересекает плоскости α и γ соответственно в точках G и Н, при этом EG = 12. Найдите длину GН.

Решение: Прямые EF и ЕH задают плоскость EFH, которая пересекает плоскости α и γ по прямым GD и FH соответственно. ∆GED

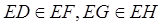
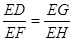
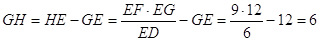
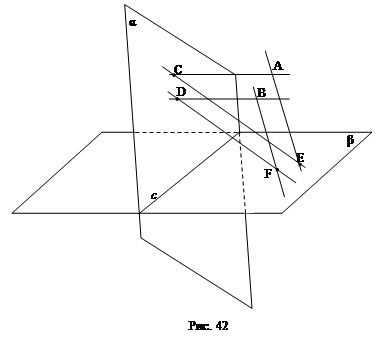
∆HEF (так как GD || FH, ). По свойству преобразования подобия: . Тогда .

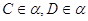
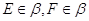
3.11. Плоскости α и β пересекаются по прямой с (рис. 42). Через точки А и В, расположенные вне этих плоскостей, проводятся параллельно плоскости β и параллельные между собой прямые АС и BD (), а также – параллельно плоскости α и параллельные между собой прямые АЕ и BF (). Докажите: а) плоскости АСЕ и BDF параллельны; б) плоскости АСЕ и BDF пересекают плоскости α и β по параллельным прямым.

Решение: а) GА || DB, АЕ || FВ по условию. По теореме о параллельности плоскостей (через пересекающиеся прямые): (АСЕ) || (DBF).

б) BF и АЕ задают плоскость, параллельную плоскости α. По свойству параллельных плоскостей: EF || с. Аналогично CD || c. По признаку параллельности прямых: CD || EF.

5.3. Уроки проверки знаний, умений и навыков

Для проверки знаний, умений и навыков разработаны три задачи на выявление типов оперирования пространственными образами: изменение пространственного положения образа (I тип); преобразование структуры образа (II тип); изменение положения и структуры образа одновременно (III тип).

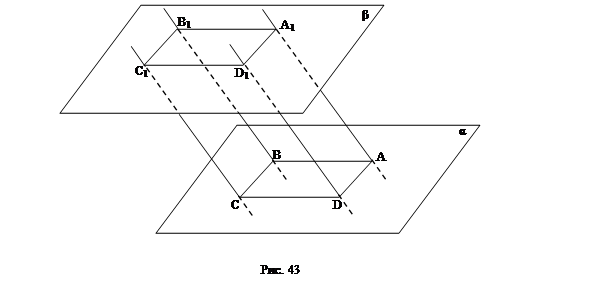
1. Через вершины параллелограмма ABCD, лежащего в одной из двух параллельных плоскостей, проведены параллельные прямые, пересекающие вторую плоскость в точках А₁, В₁, С₁ и D₁. Докажите, что четырехугольник А₁В₁С₁D₁ тоже параллелограмм (рис. 43).

Решение: АА₁ = DD₁ = СС₁ = ВВ₁ (отрезки параллельных прямых, заключенные между параллельными плоскостями, равны). Попарно параллельные прямые задают параллелограммы (задание плоскости через параллельные прямые), следовательно D₁А₁ || DА || СВ || С₁В₁. По определению А₁В₁С₁D₁ параллелограмм.

Источник

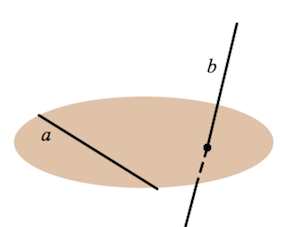
Скрещивающиеся прямые

Скрещивающиеся прямые – прямые, которые невозможно поместить в одну плоскость, то есть они не параллельны и не пересекаются.

Признак скрещивающихся прямых

Расстояние между скрещивающимися прямыми

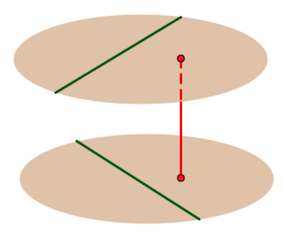
Через две скрещивающиеся прямые можно провести две параллельные плоскости (единственным образом).

Расстояние между скрещивающимися прямыми – есть расстояние между этими плоскостями.

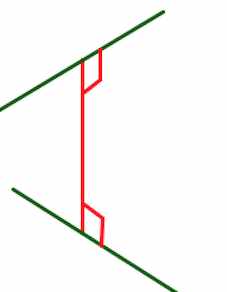
Общий перпендикуляр к двум скрещивающимся прямым

Общим перпендикуляром к двум скрещивающимся прямым называется отрезок, перпендикулярный каждой из двух скрещивающихся прямых, концы которого лежат на этих прямых.

Длина общего перпендикуляра равна расстоянию между скрещивающимися прямыми.

Угол между скрещивающимися прямыми

Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.

(Одну из прямых можно вполне и не переносить параллельно самой себе, а ограничиться только параллельным переносом одной из прямых до пересечения со второй).

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник

Стереометрия. Страница 3

Главная > Учебные материалы > Математика: Стереометрия. Страница 3

1.Перпендикулярность прямых в пространстве. 2.Признак перпендикулярности прямой и плоскости. 3.Теорема о трех перпендикулярах. 4.Признак перпендикулярности плоскостей. 5.Расстояние между скрещивающимися прямыми. 6.Примеры.

1. Перпендикулярность прямых в пространстве

Теорема. Если две пересекающиеся прямые параллельны двум перпендикулярным прямым, то они перпендикулярны и между собой.

Рис. 1 Перпендикулярность прямых в пространстве.

2.Признак перпендикулярности прямой и плоскости

Теорема. Прямая, перпендикулярная двум пересекающимся прямым на плоскости, перпендикулярна данной плоскости.

Доказательство. Пусть прямые k и b две пересекающиеся прямые на плоскости α. Прямая а перпендикулярна прямым k и b. Доказать, что прямая а перпендикулярна плоскости α. (Рис.2)

Проведем произвольную прямую х от точки А и прямую АВ, которая пересечет прямые k и b в точках К и В на плоскости α. Отложим на прямой а два равных отрезка в разные стороны АА’ и AA». Тогда треугольники АА’K и AA»K будут равны по двум сторонам и углу между ними. Так же как и треугольники АА’В и AA»В. Отсюда следует, что треугольники А’BK и А»BK равны по третьему признаку равенства треугольников. И следовательно, треугольники А’BE и A»BE равны, т.к. одна сторона у них общая ВЕ, стороны А’B и А»B равны из предыдущих рассуждений. Углы между этими сторонами также равны. Следовательно мы приходим к выводу, что треугольники А’AE и A»AE равны по трем сторонам. АЕ является медианой, биссектрисой и высотой, так как стороны А’Е и A»Е у них равные. И следовательно, угол между сторонами АА’ и АЕ равен 90°. Это значит, что прямая а перпендикулярна плоскости α.

Рис.2 Признак перпендикулярности прямой и плоскости

3. Теорема о трех перпендикулярах

Теорема: если прямая, проведенная на плоскости и проходящая через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и наклонной.

Доказательство.

Проведем прямую через основание наклонной AD и параллельную прямой СВ. Тогда прямая AD также перпендикулярна плоскости α и соответственно прямой а. Проведем плоскость β через прямые АD и CB. Тогда, если прямая а перпендикулярна проекции наклонной АВ, то она перпендикулярна плоскости β. А следовательно, любой прямой в этой плоскости, т.е. самой наклонной АС.

Следует отметить, что верно и обратное утверждение. Если прямая, проведенная на плоскости через основание наклонной ей перпендикулярна, то она перпендикулярна и проекции наклонной на эту плоскость.

Рис. 3 Теорема отрех перпендикулярах.

4. Признак перпендикулярности плоскостей

Теорема: Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость перпендикулярна их прямой пересечения и пересекает их по перпендикулярным прямым.

Пусть даны две плоскости α и β, которые пересекаются по прямой с (Рис.4). Проведем плоскость γ, которая пересекает плоскости α и β по прямым а и b. Плоскость γ перпендикулярна прямой с. Прямые а и b также перпендикулярны прямой с. Следовательно плоскости α и β перпендикулярны.

Если взять другую плоскость, параллельную плоскости γ, например плоскость γ’, которая пересекает прямую с под прямым углом, она пересечет плоскости α и β по прямым a’ и b’, которые будут параллельны прямым а и b. По теореме о перпендикулярности прямых в пространстве прямые a’ и b’ также будут перпендикулярны, как и прямые а и b. Что и требовалось доказать.

Рис. 4 Признак перпендикулярности плоскостей.

Теорема: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Проведем через точку А на плоскости α прямую b, перпендикулярную прямой а. Через прямые b и с проведем плоскость γ. Она перпендикулярна прямой а, так как прямая а перпендикулярна двум прямым b и с. Тогда плоскость β пересекает две плоскости α и γ по двум перпендикулярным прямым а и с. И пересекает прямую пересечения b под прямым углом. Следовательно плоскости α и β перпендикулярны.

Рис. 4.1 Перпендикулярность плоскостей.

5. Расстояние между скрещивающимися прямыми

Теорема. Две скрещивающиеся прямые имеют только один общий перпендикуляр, который также является перпендикуляром между параллельными плоскостями, проведенными через эти прямые.

Доказательство. Пусть а и b две скрещивающиеся прямые (Рис.5). Проведем через них две плоскости α и β, параллельные друг другу. А от прямой а проведем перпендикуляры на плоскость β. Таким образом, получим плоскость γ, которая перпендикулярна обоим плоскостям α и β и пересекает плоскость β по прямой a’. Прямые а и a’ параллельны. Прямая a’ пересекает прямую b в точке А. Следовательно, один из перпендикуляров, проведенных от каждой точки прямой а на плоскость β, т.е. отрезок АВ и есть общий перпендикуляр между прямыми а и b.

Допустим, что существует еще один общий перпендикуляр между прямыми а и b это CD. Тогда два перпендикуляра пересекают прямые а и b в точках А,В,С,D, которые в свою очередь параллельны между собой. Следовательно через них можно провести плоскость. А в этой плоскости лежат и две прямые а и b, которые также будут параллельны между собой. А это противоречит условию, т.к. прямые а и b являются скрещивающимися. Следовательно у двух скрещивающихся прямых может быть только один общий перпендикуляр.

Отсюда следует, что расстояние между двумя скрещивающимися прямыми равно длине их общего перпендикуляра.

Рис. 5 Расстояние между скрещивающимися прямыми.

5. Пример 1

Докажите, что через точку, не лежащую в данной плоскости, можно провести только одну прямую, перпендикулярную данной плоскости.

Доказательство:

Пусть дана плоскость α и точка А, не лежащая на данной плоскости. Проведем в плоскости α две пересекающиеся прямые d и c. А через их точку пересечения О проведем прямую f, перпендикулярную d и с (Рис.6).

Тогда по признаку перпендикулярности прямой и плоскости, прямая f будет перпендикулярна плоскости α. Теперь проведем прямую АВ, параллельную прямой f. Тогда АВ будет перпендикуляром к плоскости α также.

Возьмем на прямой b произвольную точку С и проведем в плоскости β прямую а, перпендикулярную прямой b. Тогда согласно аксиоме, (через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной), прямая АВ, параллельная прямой а, единственная. Т.е. перпендикуляр АВ к прямой b. Таким образом, перпендикуляр АВ единственный.

Рис.6 Задача. Докажите, что через точку, не лежащую в данной плоскости.

Пример 2

Через точку А прямой а проведены перпендикулярные ей плоскость β и прямая b. Докажите, что прямая b лежит в плоскости β.

Доказательство:

Пусть дана прямая а, перпендикулярные ей плоскость β и прямая b. Плоскость β и прямая b проходят через точку А прямой а (Рис.7). Необходимо доказать, что прямая b принадлежит плоскости β.

Проведем через две пересекающиеся прямые а и b плоскость α. Тогда две плоскости α и β пересекаются по прямой b’. Так как точка А принадлежит обоим плоскостям, то она лежит на прямой b’.

Таким образом, получается, что через точку А проходят две прямые b и b’, которые принадлежат плоскости α. Плоскость β перпендикулярна прямой а по условию задачи. А следовательно, прямая а перпендикулярна прямой b’. Отсюда следует, что через точку А проходят две прямые, лежащие в одной плоскости α, и перпендикулярные прямой а. А это невозможно. Так как через точку прямой можно провести только одну перпендикулярную ей прямую. Следовательно, прямые b и b’ совпадают. А отсюда следует, что прямая b полностью принадлежит плоскости β.

Рис.7 Задача. Через точку А прямой а проведены перпендикулярные ей плоскость β.

Пример 3

Через центр описанной около треугольника окружности проведена прямая, перпендикулярная плоскости треугольника. Докажите, что каждая точка этой прямой равноудалена от вершин треугольника.

Доказательство:

Пусть дан треугольник АВС и описанная вокруг него окружность с центром в точке О. Прямая а перпендикулярна плоскости треугольника (Рис.8). Необходимо доказать, что каждая точка прямой а равноудалена от вершин треугольника А, В и С.

Рассмотрим треугольник АВС. Вокруг него описана окружность с центром в точке О, поэтому отрезки АО, ВО и СО равны как радиусы. Теперь возьмем произвольную точку Х на прямой а. Так как прямая а перпендикулярна плоскости треугольника, то треугольники АОХ, ВОХ и СОХ равны по первому признаку равенства треугольников, т.е. по двум сторонам и углу между ними. У них сторона ОХ общая, а стороны АО, ВО и СО равны как радиусы. И углы между этими сторонами составляют 90°.

Отсюда можно сделать вывод, что стороны АХ, ВХ и СХ этих треугольников равны. Т.е. расстояние от вершин треугольника АВС до любой точки прямой а одинаковые.

Рис.8 Задача. Через центр описанной около треугольника окружности.

Пример 4

Через вершину А прямоугольника ABCD проведена прямая АК, перпендикулярная его плоскости. Расстояние от точки К до других вершин прямоугольника равны 9 см, 13 см и 15 см. Найдите АК.

Решение:

Пусть дан прямоугольник АВСD и прямая АК, перпендикулярная плоскости прямоугольника. ВК = 9 см, СК = 15 см, DK = 13 см (Рис.9). Необходимо найти АК.

Так как прямая АК перпендикулярна плоскости прямоугольника, то она перпендикулярна прямым АВ, AD и АС. Отсюда следует, что по теореме Пифагора можно составить следующие соотношения:

АВ 2 + AD 2 + AK 2 = CK 2

AK 2 = 25 или АК = 5 см.

Рис.9 Задача. Через вершину А прямоугольника ABCD.

Пример 5

Через основание трапеции проведена плоскость, отстоящая от другого основания на расстоянии 2 см. Найдите расстояние от точки пересечения диагоналей трапеции до этой плоскости, если основания трапеции относятся как 4:5 (верхнее к нижнему).

Решение:

Пусть дана трапеция АВСD. Плоскость α проведена через основание AD (Рис.10). ВС / AD = 4 / 5. Необходимо найти OO’.

Рассмотрим треугольники ВОС и AOD. Они подобны по трем углам. Коэффициент подобия составляет 4 / 5. Отсюда следует, что высоты ОЕ и ОF также относятся как 4 / 5.

Теперь рассмотрим треугольники FOO’ и FEE’. Они также подобны по трем углам. Коэффициент подобия у них составляет 5 / 9.

Таким образом, OO’ = EE’ 5 / 9 = 2*5 / 9 = 10 / 9 см.

Рис.10 Задача. Через основание трапеции проведена плоскость.

Источник