Докажите что число 13512966 не является квадратом

До этого была аналогичная задача с числом 3959604. Но для этого числа все просто. Берем число, делим сначала на наименьшее простое, т.е. 2 (проверяя предварительно признак делимости). Получаем частное. Частное опять проверяем на признак делимости на 2. Если нет. То проверяем, делится ли частное на следующее простое, т.е. 3. Если делится, делим. И т.д. В итоге получаем разложение на простые 3959604 = 2 * 2 * 3 * 3 * 3 * 3 * 11 * 11 * 101. Воспользуемся свойством. Квадрат любого целого числа содержит четное число простых сомножителей (все его простые множители имеют чётные кратности). Поэтому число 3959604 не может быть квадратом целого.

задан 6 Дек ’20 22:27

остаток от деления на 3 равен 2. а такого не бывает для полных квадратов.

@vadimm: число, оканчивающееся на 06, чётно, но не делится на 4. То есть числа вида 4n+2 квадратами не являются. Это соображение вполне годится для пятиклассника.

Второй вопрос существенно сложнее, так как там надо что-то считать. Но в принципе идея вполне понятная. Там ещё работает идея рассмотрения остатков от деления на 7, но это уже для классов постарше.

Спасибо. Но почему так получается это нужно доказать. Как это объяснить 5-ти класснику? Тут методический и педагогический вопрос.

@falcao, спасибо. Но вот не очень понятно. Числа вида 4n+2 и 23579006. Почему не является?

то есть остатка 2 у квадратов не получается.

Если брать эти свойства, то ребенку надо будет доказывать, наверное. Квадрат целого числа не может оканчиваться цифрами 2, 3, 7, 8, а также нечётным количеством нулей. Квадрат числа либо делится на 4, либо при делении на 8 даёт остаток 1. Квадрат числа либо делится на 9, либо при делении на 3 даёт остаток 1.

Для 3959604. Делится на 9. Но квадратом не является.

Не понятно. Почему это число вида 4n+2? Как ребенок должен понять, догадаться?

Забудьте про 4n+2. Каждое простое должно входить четное число раз. Если выделили какое-то одно, в данном случае 2, то число должно делиться на него четное число раз. Если нашли простое число, которое не входит четное число раз, то точно не квадрат. Полное разложение на простые не нужно.

@spades, кажется, понял. Число 23579006 делится на 2 (определяем по признаку делимости на 2). Делим 23579006 на 2. Получаем 11789503. Смотрим по признаку делимости делится ли 11789503 опять на 2. Нет. Дальше можно не продолжать. Так как сомножитель 2 будет всего один, а нужно чтобы было четное количество каждого сомножителя. Доказательство завершено. Так?

Источник

Задания Восьмой Олимпиады по математике Зима 2021 7 класс

На данной страницы размещены олимпиадные задания с решением для 7 класса.
Олимпиада по математике прошла 31 января 2021 года

Cкачать задание в формате Pdf

Посмотреть ответы на все задания олимпиады

Задача №1

X×Y×Z = 2021

Задача №2

Сколько всего пятизначных чисел, в записи которых нет нулей и единиц?

Задача №3

Вася делил все конфеты, которые ему подарили на Новый год.
Четверть конфет он сразу съел.
Одну пятую оставшихся конфет он отдал старшему брату.
После этого одну шестую оставшихся конфет он отдал младшему брату.
После чего у Васи осталось конфет вдвое меньше, чем ему подарили.
Какое наименьшее число конфет могло быть у Васи изначально?
(Каждый раз Вася отдавал целое число конфет)

Задача №4

Делится ли число 10 2021 + 2021 на 3?

Задача №5

В магазине два ноутбука стоили одинаково.
На первый ноутбук сначала сделали скидку 10%.
Потом сделали скидку 20% от новой цены. И еще раз сделали скидку 30% от новой цены.
А на второй ноутбук сделали сразу скидку 50%
Какой ноутбук в итоге стоит дешевле?

Задача №6

На плоскости расставили 2021 точку.
Далее некоторые точки соединили отрезками.
Может ли быть такое, что из каждой точки выходит различное число отрезков от 1 до 2021?

Задача №7

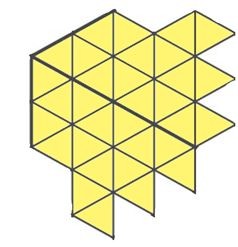
Разрежьте фигуру по линиям сетки на четыре одинаковых

Задача №8

Докажите, что число 13512966 не является квадратом

Задача №9

Имеется нарисованная прямоугольная сетка 1х1.
На этой сетке нарисовали пятно, площадь которого меньше 1.
Всегда ли можно сдвинуть и повернуть сетку так, чтобы все
ее узловые точки не были накрыты пятном?
(Форма пятна может быть любой, в том числе она может состоять из любого числа отдельных частей. При перемещении сетки клякса остаётся на месте)

Источник

Задачи повышенной трудности (9 класс)

Решение задач повышенной трудности

Алгебра 9 класс. Москва «Просвещение» 2015. Ю.М.Колягин, М.В.Ткачёва и др.

Доказать, что если натуральное число не делится на 3, то остаток от деления квадрата этого числа на 3 равен 1.

Остаток от деления на 3 этих чисел равен 1.

Доказать, что при любом натуральном п число 3п +2 не является квадратом целого числа.

Натуральные числа не являются решением этого уравнения.

Число делится на 11 тогда и только тогда, когда сумма цифр с чередующимися знаками делится на 11. Проверим число 11. 1078 на делимость на 11.

4) Доказать, что число (75*94) 26 +(39*56) 25 делится на 19.

Доказать,что если сумма цифр натурального числа не меняется при умножении его на 5, то это число делится на 9.

Натуральное число п кратное числу 9: п=9к, тогда 5п=45к, сумма цифр числа 9к равна сумме цифр числа 45к (4+5=9). Если число п не делится нацело на 9, то при умножении на 5 сумма цифр числа меняется

Так как т-1 делится на 3 п , то т-1= 3 п х, где х — натуральное число, тогда т =1+3 п х,

Доказать, что не существует целых чисел х, у, для которых справедливо равенство х 2 -у 2 =2014.

( х-у)(х+у)=2*19*53. Рассмотрим системы уравнений: 1) х-у=2 и х+у=1007, 2)х-у=19 и х+у=106, 3) х-у=38 и х+у=53, ни одна из этих систем не имеет целого решения, следовательно, не существует целых чисел х, у, для которых справедливо равенство

Допустим, что существуют натуральные числа х и у, удовлетворяющие уравнению тх+пу=тп, тогда пу=тп- тх, пу=т(п- х), следовательно, т и п — не взаимно простые, что противоречит условию. Значит, допущение неверно и не существует натуральных чисел х и у, удовлетворяющих уравнению тх+пу=тп.

Доказать, что число 7п 2 +1 не делится на 3 ни при каком натуральном п.

Доказать, что не существует целых чисел х и у удовлетворяющих уравнению 15х 2 =9+7у 2. ,

х 2 = , так как числитель дроби не делится нацело на 3, следовательно, не делится на 15, следовательно, не существует целых чисел х и у удовлетворяющих уравнению 15х 2 =9+7у 2. ,

Если т, п и к натуральные числа и т+п+к делится на 6, то т 3 +п 3 +к 3 также делится на 6.

( т+п+к) 3 и 3 ( т+п)к(т+п+к) делится на 6. Выражение 3тп(т+п) делится на 3 и на 2 при

т или п чётное, а если и т и п нечётные, то т+п- чётное.

Доказать, что если натуральные числа т и п не делятся на 5, то число т 4 -п 4 делится на 5.

Пусть т=5а+х, п=5в+у, где а, в, х, у — натуральные числа и х — остаток от деления числа т на 5, у — остаток от деления числа п на 5 могут быть числами: 1,2,3,4. т 4 -п 4 = (5а+х) 4 -( 5в+у) 4 = ( 5а) 4 +4( 5а) 3 х+6(5а) 2 х 2 +4* 5а*х 3 +х 4 -(( 5в) 4 +4( 5в) 3 у+6(5в) 2 у 2 +4( 5в)у 3 +у 4 ). Из полученных 10 одночленов на 5 не делятся х 4 и у 4 Рассмотрим разность х 4 -у 4 , если х =у, то х 4 -у 4 = 0 и число т 4 -п 4 делится на 5. Если х и у разные числа (2;1), (3;1), (4;1), (3;2), (4;2),(4;3), при всех допустимых значениях (х;у) разность х 4 -у 4 делится на 5 без остатка, следовательно, если натуральные числа т и п не делятся на 5, то число т 4 -п 4 делится на 5.

Доказать, что для любых целых чисел т и п число т 6 п 2 -п 6 т 2 делится на 30.

Если т или п кратно числу 5, то данное выражение делится на 5. Если т и п не делятся на 5, то т 4 -п 4 кратно числу 5 (№732). Если т или п чётное число, то данное выражение делится на 2. Если т и п нечётные числа, то т 4 -п 4 — чётное число и данное выражение делится на 2.

Если т или п кратно числу 3, то данное выражение делится на 3. Если т и п не кратны числу 3, то т 4 -п 4 = ( т 2 -п 2 )( т 2 +п 2 ), а т 2 -п 2 делится на 3 (№721). Следовательно, для любых целых чисел т и п число т 6 п 2 — п 6 т 2 делится на 30 (и на 60).

= = (n 2 +n)(n 2 +n+2).

Доказать, что ни при каких натуральных числах т и п не может быть верным равенство:

При т=п и при т левая часть равенства меньше правой части, при т>п левая часть равенства больше правой. Допустим, т > = n+1. Тогда (n+1 )( n+2) =п 2 +3п+2 > п 2 +2п, значит, т(т+1) > п(п+2) при m >n.

Левая часть равенства — произведение двух последовательных натуральных чисел всегда чётное число. Правая часть равенства — произведение двух последовательных натуральных чисел одинаковой чётности может быть или числом нечётным, или числом чётным. При нечётном п правая часть неравенства — нечётное число.

Доказать, что ни при каком натуральном числе п сумма п 3 +6п 2 +15п+15 не делится на п+2.

Найти все натуральные числа п, при которых число п 4 +п 2 +1 является простым.

( п 2 +1+п)( п 2 +1-п). Так как простое число имеет только 2 делителя: 1 и само число, то или

Из второго уравнения п ₁ =0, п ₂ =+1. Следовательно, только при п = 1 число п 4 +п 2 +1 является простым.

Найти четыре последовательных натуральных числа, произведение которых равно 50400

Разложим на простые множители число 5040.

5040 = 2 3 *3 2 *7, значит 5040 = 7*8*9.

Если многочлен при любом х делится на 5, то при х = 0 получим q кратно числу 5. Значит и mx 3 +nx 2 +px кратно числу 5 при любом х.

х(mx+n) при любом х есть целое число делящееся на 5, то mx+n кратно числу 5, при х = 0

п кратно числу 5, mх при любом х делится на 5 если m кратно числу 5.

Доказать, что если a,b, c- натуральные числа, то дискриминант D=b 2 -4ac квадратного трёхчлена не может принимать значение, равное 63.

Допустим b 2 -4ac =63, тогда b 2 =63+4ac, значит b нечётное число. Пусть b =2п+1, тогда ( 2п+1) 2 = 63+4ac, 4п 2 +4п+1 = 63+4ac, 4п 2 +4п-4ас = 63-1, 4п 2 +4п-4ас = 62. Правая часть равенства делится на 4 нацело, а левая нет, значит, если a,b, c — натуральные числа, то дискриминант D =b 2 -4ac квадратного трёхчлена не может принимать значение, равное 63.

Источник