Докажите что число имеющее нечетное число делителей точный квадрат

Точные квадраты и кубы

Точно так же у точного куба число делителей имеет вид 3n+1, у четвертой степени — число вида 4n+11 и т.д.

При работе со степенями целых и натуральных чисел всегда следует иметь в виду, что степень с большим показателем также является и степенью с маленьким показателем: например, а 100 — это одновременно и квадрат пятидесятой степени, и четвертая степень двадцать пятой степени, и пятая степень двадцатой степени, и т.п. Ясно, что показатель степени таким образом можно уменьшить для любого составного числа n, а для простого n это ничего не даст.

При решении задач полезным может оказаться следующее свойство точных квадратов:

Квадрат числа при делении на любое число дает тот же остаток, что и квадрат его остатка.

Например, число k при делении на 6 может давать остатки 0, 1, 2, 3, 4, 5, их квадраты — 0, 1, 4, 9, 16, 25, а остатки от деления квадратов на 6 — это 0, 1, 4, 3, 4, 1. Таким образом, квадрат числа при делении на 6 не может давать остатков 2 и 5.

Теми же рассуждениями легко получить, что возможные остатки при делении точного квадрата на 3 и на 4 — это 0 или 1.

Ответ: Все три числа в заданной сумме нечетны, следовательно, их квадраты имеют вид 4п+1, так что их сумма имеет вид 4т+3 и поэтому не является точным квадратом.

Пример 3: Доказать, что если два числа оба не делятся на 3, то их сумма не является точным квадратом.

Ответ: Так как квадрат любого натурального числа, не делящегося на 3, при делении на 3 дает остаток 1, то сумма любых двух таких чисел при делении на 3 дает остаток 2, а такое число не может быть точным квадратом.

Источник

Докажите, что число имеет нечетное количество делителей, тогда и только тогда, когда оно точный квадрат?

Докажите, что число имеет нечетное количество делителей, тогда и только тогда, когда оно точный квадрат.

Значит каждому делителю ставится в соответствие другое число являющиеся делителем следовательно число делителей будет кратно 2 то есть чётно

но если A / x = x Тогда A = x ^ 2 и прибавляется ещё один делитель т.

Е если число является полным квадратом то оно имеет нечётное количество делителей.

Найдите количество чисел от 1 до 3400, кратных 34 и имеющих ровно 2 нечетных натуральных делителя?

Найдите количество чисел от 1 до 3400, кратных 34 и имеющих ровно 2 нечетных натуральных делителя.

Докажите, что число имеет нечетное количество делителей тогда и только тогда когда оно являетса полним квадратом?

Докажите, что число имеет нечетное количество делителей тогда и только тогда когда оно являетса полним квадратом.

Какие натуральные числа имеют четное число натуральних делителей?

Чему равно произведение наибольшего нечетного делителя числа 156 и наибольшего нечетного делителя числа 68?

Чему равно произведение наибольшего нечетного делителя числа 156 и наибольшего нечетного делителя числа 68?

Чему равно произведение наибольшего нечетного делителя числа 156 и наибольшего нечетного делителя числа 68?

Чему равно произведение наибольшего нечетного делителя числа 156 и наибольшего нечетного делителя числа 68?

Может ли квадрат натурального числа иметь четное количество делителей?

Может ли квадрат натурального числа иметь четное количество делителей.

Если число можно записать в виде произведения чисел 20 и 16, тогда сколько делителей оно имеет?

Если число можно записать в виде произведения чисел 20 и 16, тогда сколько делителей оно имеет?

Даны два натуральных числа K и L?

Даны два натуральных числа K и L.

Число K имеет L делителей, а число L имеет K / 2 делителей.

Как известно, простое число имеет два делителя?

Как известно, простое число имеет два делителя.

А сколько делителей имеет квадрат простого числа?

Куб простого числа?

Четверная степень числа?

Выясните это на конкретных примерах.

Докажите, что каждое натуральное число является разностью двух натуральных чисел, имеющих одинаковое количество простых делителей?

Докажите, что каждое натуральное число является разностью двух натуральных чисел, имеющих одинаковое количество простых делителей.

(Каждый простой делитель учитывается 1 раз, например, число 12 имеет два простых делителя : 2 и 3.

Источник

Докажите что число имеющее нечетное число делителей точный квадрат

Задача 1: (6) Можно ли в прямоугольной таблице 5 × 10 так расставить числа, чтобы сумма чисел любой строки равнялась бы 30, а сумма чисел любого столбца равнялась бы 10,?

Решение: Предположим, что такая таблица существует, и подсчитаем, чему равняется сумма всех ее чисел. С одной стороны, таблица содержит 5 строк, сумма чисел в каждой из которых — 30, значит искомая сумма равна 150. С другой стороны, в таблице 10 столбцов, сумма чисел в каждом из которых — 10. Отсюда общая сумма равна 100. Полученное противоречие показывает, что такой таблицы не существует.

Задача 2: (6) Сумма нескольких чисел равна 1. Может ли сумма их квадратов быть меньше 0.1,?

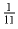
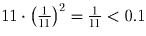
Решение: Условию задачи удовлетворяют одиннадцать чисел, равных . Их сумма равна .

Задача 3: (6–8) а) Назовите 10 первых натуральных чисел, имеющих нечетное число делителей (в число делителей включается единица и само число);

б) попробуйте сформулировать и доказать правило, позволяющее найти следующие такие числа.

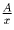
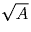
Решение: Если x — делитель числа A, то — тоже его делитель. Это простое наблюдение показывает, что каждому делителю числа A можно поставить в соответствие двойственный делитель (так, что произведение любого делителя на свой двойственный равно A). При этом очевидно, что делитель x является двойственным себе тогда и только тогда, когда x² = A. Таким образом, если число A не является полным квадратом, то все его делители разбиваются на пары двойственных друг другу, тем самым их количество четно. Если же число A является полным квадратом, то при разбиении его делителей на пары двойственных без пары останется единственный делитель . Значит, в этом случае количество делителей нечетно. Итак, натуральное число имеет нечетное число делителей тогда и только тогда, когда оно является полным квадратом. Первые десять таких чисел — 1, 4, 9, 16, 25, 36, 49, 64, 81, 100.

Задача 4: (7–8) а) Показать, что любой треугольник можно разрезать на несколько частей, из которых можно сложить прямоугольник;

б) показать, что любой прямоугольник можно разрезать на несколько частей, из которых можно сложить квадрат;

в) верно ли, что любой многоугольник можно разрезать на несколько частей, из которых можно сложить квадрат?

Решение: а) Равносоставленность (см. Т15) любого треугольника и некоторого прямоугольника следует из рис. 4 (прямая l на рисунке содержит среднюю линию треугольника).

б) Докажем сначала, что любой параллелограмм равносоставлен прямоугольнику, одна сторона которого равна основанию параллелограмма, а другая — его высоте. Если высота параллелограмма падает на его основание, то его нужно разрезать по высоте (рис. 5).

Если же она падает на продолжение основания, то тогда линиями, параллельными основанию, параллелограмм можно разрезать на параллелограммы, у которых высоты падают на основания. После этого каждый из полученных параллелограммов можно разрезать описанным выше способом (рис. 6). (Дотошный читатель сообразит, что последней оговорки можно было бы и не делать, поскольку всегда по крайней мере одна из высот параллелограмма падает на основание, а не на его продолжение; попробуйте доказать это самостоятельно.)

Теперь перейдем к доказательству основного утверждения пункта б). Для любого прямоугольника можно найти параллелограмм, у которого:

1) большая сторона равна большей стороне прямоугольника;

2) высота, опущенная на большую сторону, равна меньшей стороне прямоугольника;

3) меньшая сторона равна опущенной на нее высоте.

Способ построения такого параллелограмма приведен на рис. 7.

Согласно доказанному утверждению, этот параллелограмм равносоставлен как исходному прямоугольнику, так и квадрату со стороной, равной его меньшей стороне. Значит, исходный прямоугольник равносоставлен квадрату.

в) Докажем, что любой многоугольник можно разрезать на треугольники. Если многоугольник выпуклый, это очевидно — достаточно провести все диагонали из одной вершины. Если же он не выпуклый, то его можно разрезать на выпуклые, проведя продолжения всех его сторон. Согласно пунктам а) и б), каждый треугольник равносоставлен некоторому квадрату. Осталось доказать, что произвольные несколько квадратов можно разрезать на части, из которых можно сложить один квадрат. Как это сделать для двух квадратов, показано на рис. 8. Если квадратов больше двух, то проделав эту операцию с любыми двумя, мы уменьшим их количество на один. Повторяя ее, мы получим в конце концов один квадрат.

Источник

Олимпиадные задачи по математике «Теория чисел» ( с решением)

Олимпиадные задачи «Теория чисел»

Задача 1. Петин счет в банке содержит 500 долларов. Банк разрешает совершать операции только двух видов: снимать 300 долларов или добавлять 198 долларов.
Какую максимальную сумму Петя может снять со счета, если других денег у него нет?

Задача 2. Наибольший общий делитель (НОД) натуральных чисел m и n равен 1. Каково наибольшее возможное значение НОД чисел m+2000n и n+2000m?

Задача 3. Докажите, что произведение любых трёх последовательных натуральных чисел делится на 6.

Задача 4. Найдите все натуральные n > 1, для которых n 3 – 3 делится на n – 1.

Задача 5. Докажите, что любое натуральное число, десятичная запись которого состоит из 3 -х одинаковых цифр, делится на 37.

Задача 7 * . Докажите, что число, имеющее нечётное число делителей, является точным квадратом.

( n + 1)( n + 2)( n + 3)( n + 4) делится на 1000.

Задача 15 * . Сумма кубов трёх последовательных натуральных чисел оказалась кубом натурального числа. Докажите, что среднее из этих трёх чисел делится на 4.

Докажем, что снять 498 долларов возможно. Произведем следующие операции: 500-300=200, 200+198=398, 398-300=98, 98+198=296, 296+198=494. Сумма, лежащая в банке, уменьшилась на 6 долларов.

Проделав аналогичную процедуру 16 раз, Петя снимет 96 долларов. Затем он может снять 300, положить 198 и снова снять 300. В результате у него будет 498 долларов.

Решение задачи 3: Среди этих трёх чисел есть хотя бы одно чётное число. Значит, в разложении произведения на простые множители есть множитель 2.
Среди этих трёх чисел одно число делится на 3. Значит, в разложении произведения на простые множители есть множитель 3.
В разложении произведения на простые множители есть простые числа 2 и 3. Значит, оно делится на их произведение, то есть на 6.

Решение задачи 5: Такое число делится на 111 = 3·37.

Решение задачи 6 *: Число 8 можно представить в виде суммы трёх различных натуральных чисел двумя способами: 8 = 1 + 2 + 5 = 1 + 3 + 4. Числа 1, 3 и 4 не могут быть тремя наименьшими делителями числа A : если A делится на 4, то оно делится и на 2. Значит, три наименьших делителя A – это 1, 2 и 5. Таким образом, A делится на 10, но не делится на 4. Следовательно, число A оканчивается ровно на один нуль.
Ответ : На один нуль.

Решение задачи 9 * : Всего дано 11 чисел, а нужно вычеркнуть 10 чисел. Поэтому в конце должно остаться одно число, кратное 11, то есть число 44. С другой стороны, число 44 мы должны вычеркнуть самым первым. Действительно, сумма всех данных чисел равна 11·108 : 2, поэтому она делится на 11. Следовательно, если после вычёркивания одного числа сумма оставшихся чисел делится на 11, то вычеркнутое число тоже делится на 11.

Решение задачи10 *: Умножив такое число на 9, получим число 9010. 053, которое делится на 53, так как 901 = 53·17. Значит, и исходное число делится на 53.

Ответ : , где k – любое целое число.

Решение задачи 13 * : Предположим, что нашлись 18 хороших чисел подряд.

6( n + 2). Поскольку эти числа – хорошие, и в разложение каждого из них на

простые множители входят двойка и тройка, других простых делителей у них

быть не может. Лишь одно из трёх подряд идущих натуральных чисел n, n + 1,

n + 2 может делиться на 3. Значит, остальные два являются степенями двойки.

Но пары степеней двойки, отличающихся не более чем на два, – это только (1, 2)

и (2, 4); поэтому n ≤ 2. Однако тогда среди наших 18 чисел есть простое

число 13 (так как 6 n ≤ 13 ≤ 6( n + 2)), не являющееся хорошим. Противоречие.

Источник

Применение свойств квадрата целого числа в решении задач на делимость

Разделы: Математика

Цель: формирование знаний, умений и навыков при решении в целых числах уравнений, содержащих квадрат целого числа; создание условий для преодоления у выпускников трудностей при решении заданий ( ) ЕГЭ по математике.

Задачи:

Тип занятия: урок изучения нового материала.

Ход урока

I. Постановка цели

В 2009-2010 учебном году на ЕГЭ по математике задания в основном состояли из задач на делимость. Большинство выпускников 11-х классов даже не приступали к этим задачам, увидев в них нагромождение различных символов, функций и значков. Для решения таких задач необходимо знать некоторые свойства делимости целых чисел и овладеть приёмами применения этих свойств. Сегодня на занятии мы решим ряд задач на делимость, в которых используются простейшие свойства точного квадрата числа.

II. Актуализация опорных знаний

При решении задач нам пригодятся признаки делимости чисел, с которыми вы познакомились ещё в 6-ом и последующих классах, а также определение числа

Напомните, пожалуйста, признаки делимости:

И ещё вопрос: что такое и как найти значения 1!, 2!, 3!, 4!, 5!, 6!, … Посмотрите, как изменяется последняя цифра числа

n! = 123456…n – произведение первых n натуральных чисел.
1! = 1
2! = 12 = 2
3! = 123 = 6
4! = 1234 = 24
5! = 12345 = 120
6! =123456 = 720 и т.д.

При n≥5 число n! всегда оканчивается нулём.

III. Ознакомление с новым материалом

Рассмотрим таблицу квадратов натуральных чисел. Все свойства точного квадрата числа спрятаны в этой таблице. Нам только надо проявить наблюдательность при анализе данных в таблице.

к	1	2	3	4	5	6	7	8	9	10	11	12	13	14	…
	1	4	9	16	25	36	49	64	81	100	121	144	169	196	…

Обратите внимание на последние цифры квадратов чисел. Что вы заметили?

На какие натуральные числа может делиться точный квадрат числа?

Свойства квадрата целого числа

Точный квадрат целого числа не может оканчиваться цифрами 2, 3, 7, 8, а также нечётным количеством нулей.
Первое свойство очевидное и доказательства не требует.

Квадрат натурального числа либо делится на 4, либо при делении на 8 даёт остаток 1.
Доказательство:
Если а – число чётное, то есть а = 2к, то = 4 – делится на 4.
Если а – число нечётное, то есть а = 2к + 1, то = ( = 4 + 4к + 1 = 4к (к+1) + 1 – при делении на 8 даёт остаток 1.

Квадрат натурального числа либо делится на 9, либо при делении на 3 даёт остаток 1.
Доказательство:
Если число а кратно 3, значит а = 3к, тогда = ( = 9— делится на 9.
Если же число а не кратно 3, то оно имеет вид а = 3к ± 1, тогда = (= 9 ± 6к + 1 = 3к (3к±2) + 1 – при делении на 3 даёт остаток 1.

Вот мы и сформулировали свойства точного квадрата числа. Теперь вашему вниманию я предлагаю ряд задач, в решении которых используются вышеперечисленные свойства.

1. Найти все натуральные n, при которых число является точным квадратом.

Решение:

Если n=1, то – не является точным квадратом.
Если n=2, то – не является точным квадратом.
Если n=3, то – не является точным квадратом.
Если n=4, то , значит, при n=4 число является точным квадратом числа.
Если , то оканчивается 0, тогда оканчивается 7, но по свойству (1) квадрат целого числа не может оканчиваться цифрой 7. Значит, других натуральных чисел n, удовлетворяющих данному условию, не существует.

Ответ: при n=4.

Эта задача могла быть сформулирована иначе:

Решить в целых числах уравнение .

Способ решения тот же. Только надо помнить, что по определению

Ответ: .

2. Решить в целых числах уравнение: .

Решение:

Так как – произведение первых натуральных чисел, значит, , а целым может быть только k.
Если n=1, то
Если n=2, то
Если n=3, то
Если n=4, то

Но по свойству (1) квадрат целого числа не может оканчиваться ни 3, ни 8, значит, других целых решений уравнение не имеет.

Ответ: .

3. Решить в целых числах уравнение: .

Решение:

В решении этого уравнения надо использовать тот же приём, что и в предыдущих. Его легко решить устно.

Но тогда оканчивается 8 или 3, а это противоречит свойству (1). Значит, при уравнение не имеет решений в целых числах. Поэтому решения уравнения следует искать для
Если n=1, то
Если n=2, то .
Если n=3, то .
Если n=4, то .
Как видим, ни при каком число не является точным квадратом.

Ответ: уравнение не имеет целых решений.

4. Решить уравнение в целых числах: .

Решение:

, и опираемся на свойство(1) квадрата целого числа.

Значит, оканчивается 7, но тогда и оканчивается 7.
Но квадрат целого числа не может оканчиваться 7, значит, целых решений нет.
Значит, решения уравнения следует искать при = 1, 2, 3, 4.
Если n=1, то
Если n=2, то
Если n=3, то
Если n=4, то

Ответ: .

5. Решить в натуральных числах уравнение .

Решение:

В этом уравнении должны быть натуральными числами, а в остальном – решение аналогично предыдущим.

Но квадрат целого числа не может оканчиваться 3, значит, при натуральных решений уравнение не имеет. Остаётся проверить наличие решений при =1, 2, 3, 4.
Если n=1, то
Если n=2, то
Если n=3, то
Если n=4, то

Ответ:

6. Решить уравнение в целых числах: 1!+2!+3!+…+

Решение:

Если =1, то 1! =, тогда
Если =2, то 1!+2! = – число не целое.
Если =3, то 1!+2!+3! =
Если =4, то 1!+2!+3!+4! = – число не целое.
Если , то 1!+2!+3!+4!+…+х! оканчивается цифрой 3, но квадрат целого числа не может оканчиваться 3.
Значит, при

Ответ: =1, 2)=3,

7. Доказать, что уравнение не имеет решений в целых числах.

Доказательство:

если делится на 5, а это возможно, если оканчивается 0 или 5, тогда

Но квадрат целого числа не может оканчиваться ни цифрой 3, ни цифрой 8.

Значит, уравнение не имеет целых решений. Что и требовалось доказать.

8. Решить в целых числах уравнение .

Решение:

Если n=1, то
Если n=2, то
Если n=3, то
Если n=4, то
Если уравнение целых решений не имеет, так как при чётном
1234… (1234… ( =
=1234… (
При нечётном
1234… (1234… ( =1234… ( – не делится на 4, а при делении на 8 даёт остаток 3, а не 1.

Ответ: 1)

9. Решить уравнение в целых числах: .

Решение:

Если =1, то

Если =4, то
При (1245… +1) = – левая часть уравнения делится на 3, значит, число должно делиться на 9.
Но 1245… +1 на 3 не делится, поэтому левая часть уравнения не кратна 9 Значит, при уравнение не имеет целых решений.

Ответ: 1) =1, =4,

10. Решить в целых числах уравнение:

Решение:

1) Если m – число чётное, то – числа нечётные и их произведение
– тоже число нечётное, но правая часть уравнения – чётное число. Значит, при чётном m уравнение не имеет решений.
2) Если m – число нечётное, то – числа чётные, причем, – два последовательных чётных числа, одно из которых кратно 2, а другое – 4. Тогда , значит, , но квадрат целого числа делится на 4 или при делении на 8 даёт остаток 1. А лишь в единственном случае, если n=0. При n=0 уравнение примет вид:

Ответ: .

11. Решить в целых числах уравнение:

Решение:

1) Если n – число четное, то – числа нечётные, значит, – тоже нечетное число, а это возможно лишь тогда, когда , т.е. . При всех других чётных уравнение целых решений не имеет.
2) Если n – число нечётное, то – два последовательных чётных числа, одно из которых кратно 2, а другое – 4. Тогда их произведение . Значит, и левая часть уравнения
, но – число нечётное, значит, только
. Это возможно, если . При .
При ,
.
Если же , то , а правая часть уравнения , значит, других решений уравнение не имеет.

Ответ: 1) 2)

12. Решить в целых числах уравнение:

Решение:

– имеет решение, если:
1) = 0, тогда
— число нечётное, . Тогда, ,

.
() – нечётное число при . Значит, тоже должно быть нечётным, а это возможно, если . Тогда при исходное уравнение примет вид .

Ответ: 1) ; 2)

13. Доказать, что число, оканчивающееся двумя одинаковыми цифрами, отличными от 0 и 4, не может быть точным квадратом.

Доказательство:

Так как квадрат любого числа может оканчиваться цифрами: 0; 1; 4; 5; 6; 9, то кроме 0 и 4 последними цифрами могут быть: 11; 55; 66; 99.

— число чётное, тогда .

Значит, не существует таких чисел , что оканчивается 55, 66, 11 или 99.

Что и требовалось доказать.

14. Доказать, что тысячезначное число, все цифры которого пятёрки, за исключением, быть может, одной, не является точным квадратом.

Доказательство:

а) Если число оканчивается 5, то предпоследняя цифра может быть только 2, тогда 55….525 – число нечётное, оно не кратно 4, значит, при делении на 8 должно дать в остатке 1, но . Значит, число не может быть точным квадратом.
б) Если последняя цифра не 5, то это может быть 0; 1; 4; 6; 9, тогда
– не может быть, т.к. оканчиваться чётным числом нулей.
– не может быть, т.к. .
– чётно, но не кратно 4, т.к. 54 не делится на 4.
– нечётное, но при делении на 8 даёт остаток 7, а не 1.
– чётно и делится нацело на 4, но не всякое чётное число, кратное 4, является точным квадратом. Проверим, выполняется ли свойство (3) квадрата целого числа.
сумма цифр не делится на 9, а при делении на 3 в остатке 0.

Таким образом, ни одно из перечисленных чисел не может быть точным квадратом. Что и требовалось доказать.

Источник