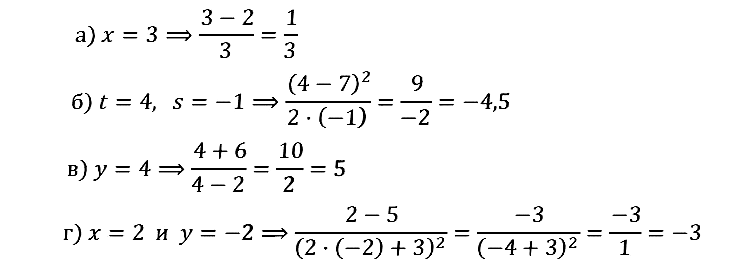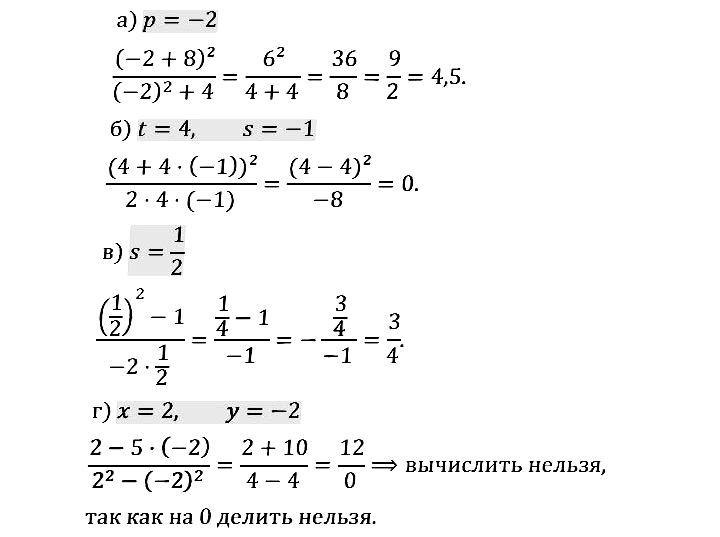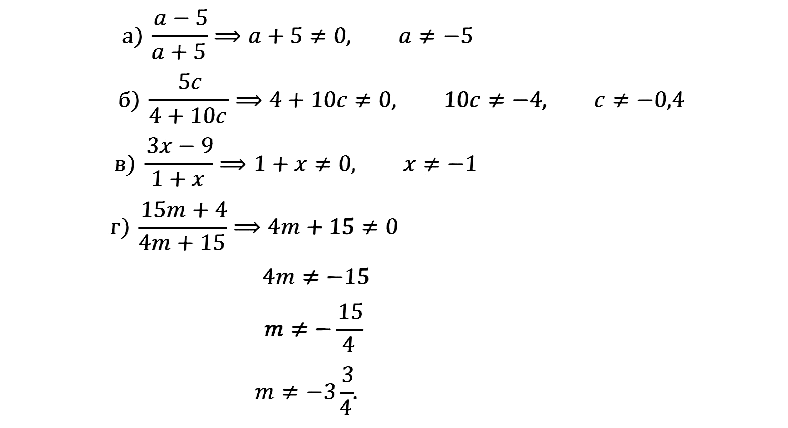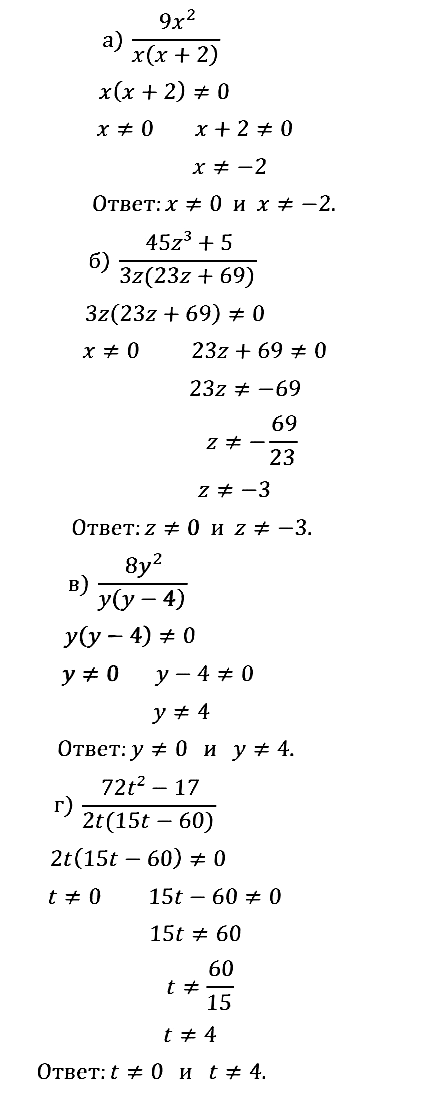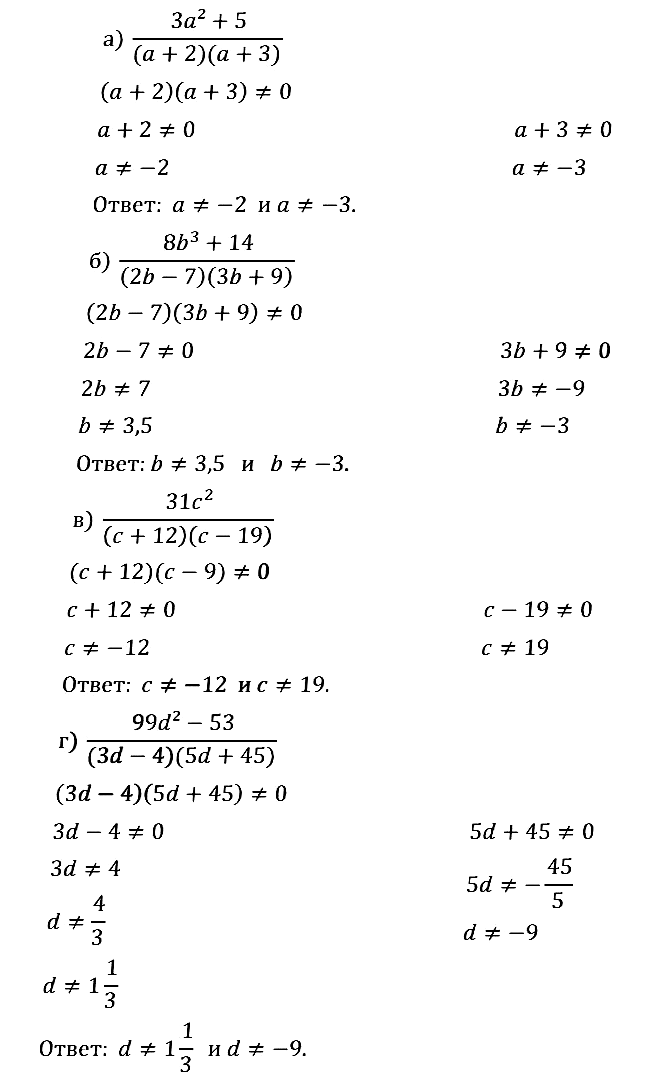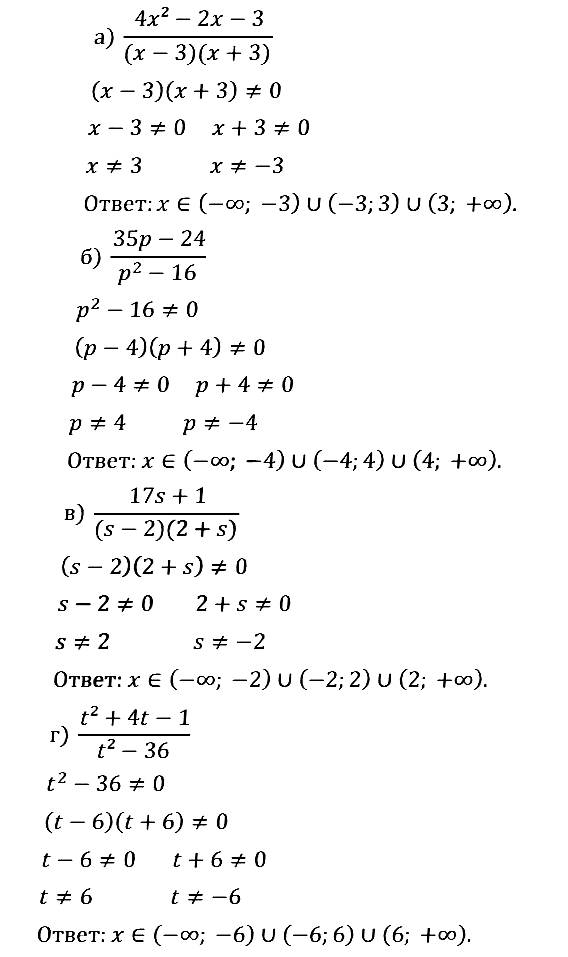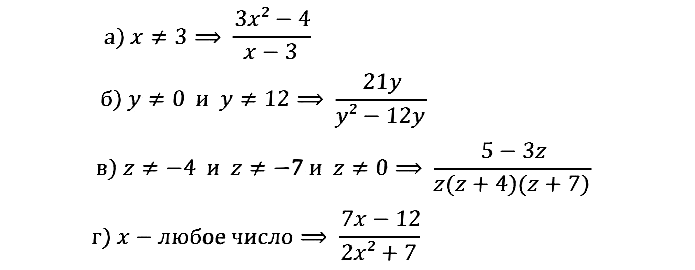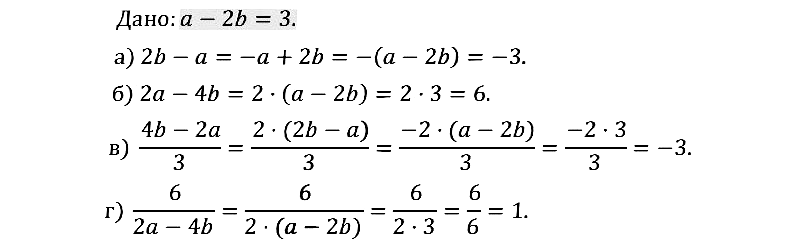Докажите что данная дробь не имеет смысла алгебра 7 класс
Докажите что данная дробь не имеет смысла алгебра 7 класс
В курсе алгебры 7 класса мы занимались преобразованиями целых выражений, т. е. выражений, составленных из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля. Так, целыми являются выражения
В отличие от них выражения
помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными. Такие выражения называют дробными выражениями.
Целые и дробные выражения называют рациональными выражениями.
Целое выражение имеет смысл при любых значениях входящих в него переменных, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны.
Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение не имеет смысла
при а = 0. При всех остальных значениях а это выражение имеет
смысл. Выражение имеет смысл при тех значениях х и у, x ≠ y.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Выражение вида называется, как известно, дробью.
Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.
Примерами рациональных дробей служат дроби
В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.
Пример 1. Найдем допустимые значения переменной в дроби
Это уравнение имеет два корня: 0 и 9. Следовательно, допустимыми значениями переменной а являются все числа, кроме 0 и 9.
Дробь равна нулю тогда и только тогда, когда a = 0 и b ≠ 0.
2. Основное свойство дроби. Сокращение дробей
Мы знаем, что для обыкновенных дробей выполняется следующее свойство: если числитель и знаменатель дроби умножить на одно и то же натуральное число, то значение дроби не изменится. Иначе говоря, при любых натуральных значениях а, b и с верно paвенство
Докажем, что это равенство верно не только при натуральных, но и при любых других значениях а, b и с, при которых знаменатель отличен от нуля, т. е. при b ≠ О и с ≠ О.
Пусть Тогда по определению частного а = bm. Умножим обе части этого равенства на с :
На основании сочетательного и переместительного свойств умножения имеем:
Так как bс ≠ 0, то по определению частного
Мы показали, что для любых числовых значений переменных b и с, где b ≠ О и с ≠ 0, верно равенство
Равенство (1) сохраняет силу и в том случае, когда под буквами а, b и с понимают многочлены, причем b и с — ненулевые многочлены, т. е. многочлены, не равные тождественно нулю.
Равенство (1) выражает основное свойство рациональной дроби:
если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.
Это равенство верно при всех допустимых значениях переменных. Такие равенства будем называть тождествами. Ранее тождествами мы называли равенства, верные при всех значениях переменных. Теперь мы расширяем понятие тождества.
Определение. Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.
Основное свойство рациональной дроби позволяет выполнять приведение дроби к новому знаменателю и сокращение дробей. Приведем примеры.
Пример 1. Приведем дробь к знаменателю
Множитель называют дополнительным множителем к числителю и знаменателю дроби
Пример 2. Приведем дробь к знаменателю
Для этого числитель и знаменатель данной дроби умножим на -1:
если изменить знак числителя (или знак знаменателя) дроби и знак перед дробью, то получим выражение, тождественно равное данному.
Пример 3. Сократим дробь
Разложим числитель и знаменатель дроби на множители:
Сократим полученную дробь на общий множитель a + 3:
Пример 4. Построим график функции
Графиком функции является прямая, а графиком функции но с «выколотой» точкой (4 ; 4) (рис. 1.)
Алгебра 8 Мордкович (упр. 1.1 — 1.41)
Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович ( 2018-2020 ). Глава I Алгебраические дроби. § 1. Основные понятия. ОТВЕТЫ на упражнения 1.1 — 1.41. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.
Алгебра 8 Мордкович (упр. 1.1 — 1.41)
§ 1. Основные понятия
Является ли алгебраической дробью выражение:
№ 1.2. а) (7a 2 + 4)/14; б) (2f 2 + 6f + 15)/2f – 5f; в) 3t – p 2 /t 2 ; г) (6nm + 3m 2 n 2 )/(7n – 12m).
Найдите значение алгебраической дроби:
№ 1.3. а) (x – 2)/x при x = 3; б) (t – 7) 2 /2s при t = 4, s = –1; в) (y + 6)/(y – 2) при y = 4; г) (x – 5)/(2y + 3) 2 при x = 2, y = –2.
№ 1.4. а) (p + 8) 2 /(p 2 + 4) при p = –2; б) …
Установите, при каких значениях переменной не имеет смысла алгебраическая дробь:
№ 1.5. а) (а – 5)/(а + 5); б) 5с/(4 + 10с); в) …
№ 1.6. a) 9х 2 /(x(x + 2)); б) …
№ 1.7. a) (3а 2 + 5) / ((а + 2)(а + 3)); б) …
№ 1.8. Найдите допустимые значения переменной для заданной алгебраической дроби: 
№ 1.9. Придумайте примеры алгебраических дробей, которые имели бы смысл при: а) х ≠ 3; б) у ≠ 0, у ≠ 12; в) z ≠ –4, z ≠ –7, z ≠ 0; г) любом значении х.
Найдите значения переменной, при которых алгебраическая дробь равна нулю (если такие значения существуют):
№ 1.10. 
№ 1.11. 
№ 1.12. Зная, что a – 2b = 3, найдите значение выражения: а) 2b – а; б) 2а – 4b; в) (4b – 2a)/3; г) 6/(2a – 4b). Составьте математическую модель ситуации, описанной в условии задачи:
№ 1.13. Туристы прошли 6 км по лесной тропе, а затем 10 км по шоссе, увеличив при этом свою скорость на 1 км/ч. На весь путь они затратили 3,5 ч.
№ 1.14. Прогулочный катер двигался по реке, скорость течения которой 2 км/ч. По течению реки он проплыл 18 км, а против течения 14 км, затратив на весь путь 1 ч 20 мин.
№ 1.15. Из пункта А в пункт В, находящийся на расстоянии 120 км от пункта А, выехали одновременно два автомобиля. Скорость одного из них на 20 км/ч больше скорости другого, поэтому он приехал в пункт В на 1 ч раньше.
№ 1.16. Из города в посёлок, находящийся на расстоянии 40 км от города, выехал грузовик, а через 10 мин вслед за ним отправился легковой автомобиль, скорость которого на 20 км/ч больше скорости грузовика. В посёлок они прибыли одновременно.
№ 1.17. С двух турбаз одновременно вышли две группы туристов, которые должны были встретиться на берегу реки. До этого места первой группе нужно идти 12 км, а второй – 10 км. Известно, что скорость первой группы была на 1 км/ч меньше скорости второй и что она прибыла на берег реки на 1 ч позже второй группы.
Решите задачу, выделяя три этапа математического моделирования:
№ 1.18. Моторная лодка, собственная скорость которой равна 30 км/ч, прошла по течению реки расстояние 48 км и против течения 42 км. Какова скорость течения реки, если известно, что на путь по течению лодка затратила столько же времени, сколько на путь против течения?
№ 1.19. Автобус проходит расстояние 160 км за время, которое автомобиль тратит на прохождение 280 км. Найдите скорость автобуса, если известно, что она на 30 км/ч меньше скорости автомобиля.