Докажите что диаметр проходящий через середину хорды перпендикулярен ей ОКРУЖНОСТЬ И КРУГ. ЦИЛИНДР.
§ 70. ДИАМЕТР, ПЕРПЕНДИКУЛЯРНЫЙ К ХОРДЕ.
Теорема 1. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею дуги пополам.
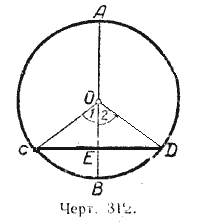
Пусть диаметр АВ перпендикулярен к хорде СD (черт. 312). Требуется доказать, что
Соединим точки С и D с центром окружности О. В равнобедренном треугольнике / 1 = / 2. Но / 1 и / 2 суть центральные углы. Отсюда равны и соответствующие им дуги, а именно
Теорема 2 (обрaтная). Диаметр, проведённый через середину хорды, не проходящей через центр, перпендикулярен к ней и делит дуги, стягиваемые хордой, пополам.
Пусть диаметр АВ делит хорду СD пополам. Требуется доказать, что АВ_|_СD,
Теорема 3 (обратная).Диаметр, проведённый через середину дуги, делит пополам хорду, стягивающую эту дугу, и перпендикулярен к этой хорде.
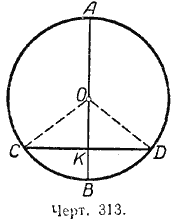
Пусть диаметр АВ делит дугу СВD пополам (черт. 313). Требуется доказать, что
Соединим центр круга О с точками С и D. В равнобедренном треугольнике СОD отрезок ОК является биссектрисой угла СОD, так как по условию теоремы
Источник
Отрезки и прямые, связанные с окружностью. Теорема о бабочке
Отрезки и прямые, связанные с окружностью Фигура Рисунок Определение и свойства Окружность Конечная часть плоскости, ограниченная окружностью
Отрезок, соединяющий центр окружности с любой точкой окружности
Отрезок, соединяющий две любые точки окружности
Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой
Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу проведённому в точку касания
Прямая, пересекающая окружность в двух точках
Круг Конечная часть плоскости, ограниченная окружностью
Радиус Отрезок, соединяющий центр окружности с любой точкой окружности
Хорда Отрезок, соединяющий две любые точки окружности
Диаметр Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой
Касательная Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу проведённому в точку касания
Секущая Прямая, пересекающая окружность в двух точках
Свойства хорд и дуг окружности Фигура Рисунок Свойство Диаметр, перпендикулярный к хорде Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. Диаметр, проходящий через середину хорды Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. Равные хорды Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности . Хорды, равноудалённые от центра окружности Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. Две хорды разной длины Большая из двух хорд расположена ближе к центру окружности. Равные дуги У равных дуг равны и хорды. Параллельные хорды Дуги, заключённые между параллельными хордами, равны.
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности .
Хорды, равноудалённые от центра окружности Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины Большая из двух хорд расположена ближе к центру окружности.
Равные дуги У равных дуг равны и хорды.
Параллельные хорды Дуги, заключённые между параллельными хордами, равны.
Теоремы о длинах хорд, касательных и секущих Фигура Рисунок Теорема Пересекающиеся хорды Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Касательные, проведённые к окружности из одной точки Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Касательные, проведённые к окружности из одной точки Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Доказательства теорем о длинах хорд, касательных и секущих
Тогда справедливо равенство
откуда и вытекает требуемое утверждение.
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
откуда и вытекает требуемое утверждение.
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Теорема о бабочке
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.
Источник
Популярная книга Спаси нас доступна для чтения прямо сейчас на нашем сайте boochi.ru. Скачать книгу в формате FB2, TXT, PDF, EPUB бесплатно без регистрации. Популярная книга Спаси себя доступна для чтения прямо сейчас на нашем сайте boochi.ru. Скачать книгу в формате FB2, TXT, PDF, EPUB бесплатно без регистрации. Популярная книга Спаси меня доступна для чтения прямо сейчас на нашем сайте boochi.ru. Скачать книгу в формате FB2, TXT, PDF, EPUB бесплатно без регистрации. Популярная книга Судьба по книге перемен доступна для чтения прямо сейчас на нашем сайте boochi.ru. Скачать книгу в формате FB2, TXT, PDF, EPUB бесплатно без регистрации. Популярная книга Орден Архитекторов 6 доступна для чтения прямо сейчас на нашем сайте boochi.ru. Скачать книгу в формате FB2, TXT, PDF, EPUB бесплатно без регистрации.












 Отрезки и прямые, связанные с окружностью
Отрезки и прямые, связанные с окружностью Свойства хорд и дуг окружности
Свойства хорд и дуг окружности Теоремы о длинах хорд, касательных и секущих
Теоремы о длинах хорд, касательных и секущих Доказательства теорем о длинах хорд, касательных и секущих
Доказательства теорем о длинах хорд, касательных и секущих Теорема о бабочке
Теорема о бабочке