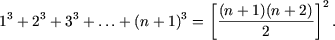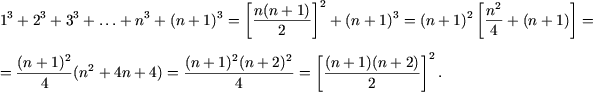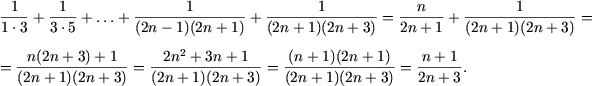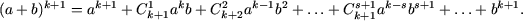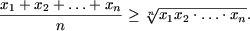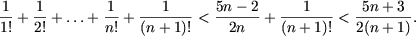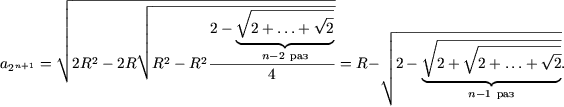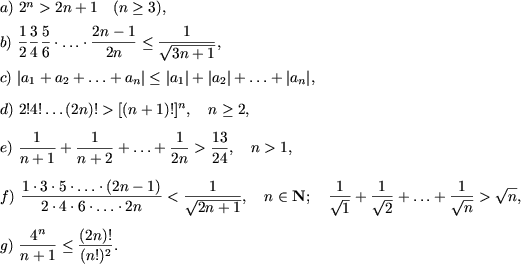Докажите что для любого натурального числа n справедливо равенство
Докажите что для любого натурального числа n справедливо равенство
Применяя метод математической индукции, доказать, что для любого натурального n справедливы следующие равенства:
а) ;
б) .
а) При n = 1 равенство справедливо. Предполагая справедливость равенства при n, покажем справедливость его и при n + 1. Действительно,
что и требовалось доказать.
б) При n = 1 справедливость равенства очевидна. Из предположения справедливости его при n следует
т. е. утверждение справедливо и при n + 1.
Пример 1. Доказать следующие равенства
Решение. a) При n = 1 равенство примет вид 
Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n.
Используя предположение индукции, получим
Таким образом, P(n + 1) истинно и, следовательно, требуемое равенство доказано.
Замечание 3. Этот пример можно решить (аналогично предыдущему) без использования метода математической индукции.
c) При n = 1 равенство истинно: 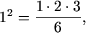
d) При n = 1 равенство справедливо: 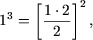
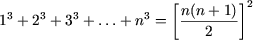
e) Утверждение P(1) справедливо: 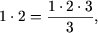
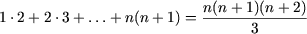
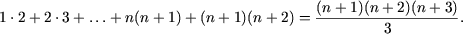
Следовательно, исходное равенство имеет место для любого натурального n.
f) P(1) справедливо: 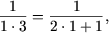
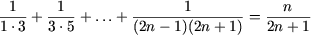
Действительно, учитывая, что P(n) имеет место, получим
Таким образом, равенство доказано.
g) При n = 1 имеем a + b = b + a и, следовательно, равенство справедливо.
Пусть формула бинома Ньютона справедлива при n = k, то есть,
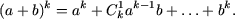
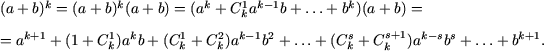
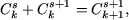
Пример 2. Доказать неравенства
Решение. a) При n = 1 получаем истинное неравенство
Таким образом, если P(n) истинно, то и P(n + 1) истинно, следовательно, согласно принципу математической индукции, неравенство Бернулли справедливо.
Рассмотрим следующие два случая:
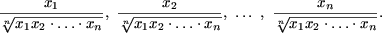
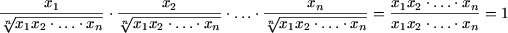
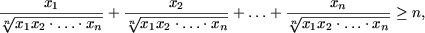
sin 2n a + cos 2n a ≤ 1 и покажем, что имеет место P ( n + 1). Действительно, sin 2(n + 1) a + cos 2(n + 1) a = sin 2n a ·sin 2 a + cos 2n a ·cos 2 a 2n a + cos 2n a ≤ 1 (если sin 2 a ≤ 1, то cos 2 a 2 a ≤ 1, то sin 2 a n О N sin 2n a + cos 2n ≤ 1 и знак равенства достигается лишь при n = 1.
e) При n = 1 утверждение справедливо: 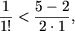
Допустим, что 
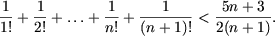
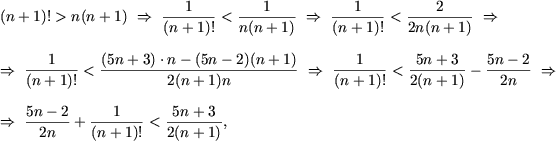
Поскольку при n > 10 имеем 
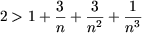
Пример 3. Доказать, что для любого n О N

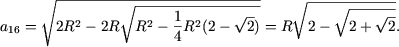
 | (2) |
Как ранее было показано при n = 1, что эта формула справедлива. Пусть (2) выполняется при n = k. Вычислим 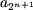
Замечание. Из (2) следует, что длина окружности равна
I. Доказать равенства
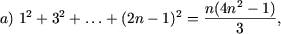 |
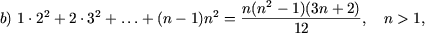 |
 |
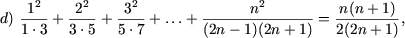 |
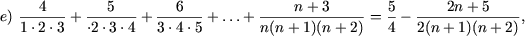 |
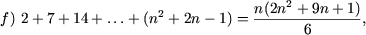 |
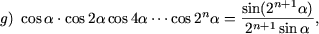 |
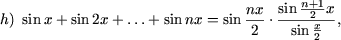 |
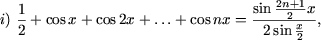 |
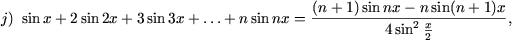 |
 |
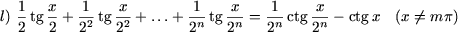 |
 |
II. Доказать неравенства
III. Доказать, что при любом натуральном n число an делится на b
IV. Показать, что 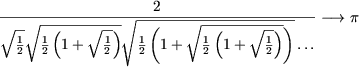
VI. Пусть даны n произвольных квадратов. Доказать, что эти квадраты могут быть разрезаны так, чтобы из получившихся частей можно было образовать квадрат.
Докажите что для любого натурального числа n справедливо равенство
Применяя метод математической индукции, доказать, что для любого натурального n справедливы следующие равенства:
а) ;
б) .
а) При n = 1 равенство справедливо. Предполагая справедливость равенства при n, покажем справедливость его и при n + 1. Действительно,
что и требовалось доказать.
б) При n = 1 справедливость равенства очевидна. Из предположения справедливости его при n следует
т. е. утверждение справедливо и при n + 1.
Примеры по теме «Математическая индукция»
Пример 1. Найти сумму S n первых n нечетных чисел:
В таких ситуациях обычно начинают рассматривать частные случаи:
S 4 = 1 + 3 + 5 + 7= 16; S 5 = 1 + 3 + 5 + 7 + 9 = 25.
Какой вывод можно сделать на основе этих частных случаев? В данном случае высказать гипотезу несложно:
сумма первых п нечетных чисел равна квадрату их числа, т. е. квадрату числа складываемых нечетных чисел: S n = п 2 .
Пример 2. Пусть требуется найти
для каждого натурального п.
Рассмотрим частные случаи: S1 = 3, S 2 = 18.
Попробуем доказать справедливость этого утверждения методом математической индукции.
S 1=1 • 3 = 3 • 1 ·(2 • 1-1) — равенство верно.
2. Индуктивное предположение: Пусть формула
верна для некоторого произвольного k > 1.
3. Индуктивный переход. Надо доказать справедливость равенства
S k +1=3 k (2 k –1) + (2 k +1)(2 k + 3) = 10 k 2 + 5 k + 3,
но нам нужно было получить
S k +1 = 3( k + 1)(2 k + 1) = 6 k 2 + 9 k + 3.
Так как у нас получился иной результат, то высказанное предположение неверно; на самом деле справедлива формула
Пример 3. Доказать, что при любых натуральных п число 7 n + 12п+ 17 делится на 18.
1. При n = 1 число 7 1 + 12 • 1 + 17 = 36 кратно 18.
2. Предположим, что для некоторого натурального числа k ≥ 1 число
7 k + 12 k + 17 делится на 18.
3. Рассмотрим число 7 k +1 + 12( k + 1) + 17 и докажем, что оно кратно 18.
Мы видим, что при любом натуральном k число 6 • 12 k + 90 = 18(4 k + 5)
кратно 18. Итак, мы представили число 7 k +1 +12( k + 1) + 17 в виде разности двух чисел, каждое из которых делится на 18. Следовательно, и
само число 7 k +1 + 12( k + 1) + 17 кратно 18.
(32 > 25), значит, утверждение А(5) верно.
3. Индуктивный переход. Докажем справедливость неравенства
Запишем последнее неравенство в виде
т. е. требуемое неравенство.
Итак, согласно принципу математической индукции данное неравенство справедливо при всех натуральных n > 4.
Пример5.Доказать, что при всех натуральных п справедливо
В данном случае проверим наше неравенство для п = 1 и п = 2.
1. При п = 1 неравенство 4 1 > 7 • 1-5 верно. При п = 2 имеем
4 2 > 7 • 2-5 также верное неравенство.
Но при любом k ≥2 число
Следовательно, справедливо неравенство
Из неравенств (1) и (3) следует неравенство
Теперь, пользуясь принципом математической индукции, данное утверждение справедливо для всех натуральных чисел.
Замечание. В данном случае базис индукции — пункт 1 — содержит доказательство данного утверждения для первых двух натуральных чисел n = 1 и n = 2. Это связано с тем, что неравенство (2) не выполняется при k = 1, но справедливо при каждом натуральном k > 1. Поэтому, доказав данное неравенство для n = 1и n = 2, в дальнейшем рассматривались числа k ≥2.
Пример 6. Доказать, что если для n положительных чисел а1, а2. а n ( n > 1) выполнено условие a 1а2. а n =1, то
Предположение индукции. Пусть данное утверждение справедливо для всех
3. Индуктивный переход. Докажем, что если произведение k + 1 положительных чисел равно 1, т. е. а1а2. а k +1= 1, то их сумма не меньше количества слагаемых:
Отметим, что если все данные числа равны между собой, то каждое из них равно 1 и неравенство (6), очевидно, выполняется. Предположим, что хотя бы одно из заданных положительных чисел меньше 1, например, 0 a k +1 k > 1 (если какие-то другие два числа обладают указанными свойствами, то мы просто их перенумеруем).
Рассмотрим произведение k чисел: а1, a 2. а k -1( a k a k +1) = 1. По условию все эти числа положительны:
значит, по предположению индукции имеем
Чтобы доказать неравенство (6), перепишем неравенство (7) следующим образом:
Для доказательства неравенства (6) осталось доказать, что
Левую часть последнего неравенства можно записать так:
Тогда неравенство (8) с учетом (9) примет вид
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №27. Математическая индукция.
Индукция; принцип математической индукции; полная индукция; неполная индукция.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Если рассмотреть значения квадратного трехчлена 




Мы проверили справедливость утверждения при n от 1 до 14. Возьмем n равное 41 и подставим в наш квадратный трехчлен.
При n = 41, получаем

Получили составное число, т.е. противоречие нашему утверждению.
Для строгого доказательства утверждений на множестве натуральных чисел используют метод полной математической индукции. Продемонстрируем этот метод на примере:
Первым шагом проверим базу индукции, т.е. справедливость неравенства при наименьшем натуральном числе n=1

Вторым шагом будет индуктивное предположение, т.е. предположим, что неравенство верно для некоторого натурального n.
2 шаг: предположим, что неравенство верно при некотором натуральном n.

Далее выполним индуктивный переход, т.е. докажем, что из предположения, сделанного на втором шаге следует справедливость аналогичного неравенства для следующего натурального числа n+1


Получим верное неравенство
Но!
Т.к.
Из 
Т.о. доказательство методом полной математической индукции состоит в:
1) Проверке справедливости утверждения при 
2) Доказательстве, что если утверждение верно для натурального числа 

Доказать, что для любого натурального значения n справедливо равенство
Докажем, что если неравенство верно для некоторого n, то оно верно и для 
Прибавим к обеим частям верного по предположению равенства число 
Преобразуем правую часть равенства:
Таким образом из справедливости равенства
Следует справедливость равенства
Докажите, что 
1 шаг: при

2 шаг: предположим, что сумма 
3 шаг:докажем, что 
В ходе преобразований получаем сумму, которая делится на 133 без остатка, т.к. первое ее слагаемое