Докажите что движение в пространстве переводит плоскость в плоскость

Стереометрия. Страница 4

Главная > Учебные материалы > Математика: Стереометрия. Страница 4

1.Декартовы координаты в пространстве. 2.Расстояние между двумя точками. 3.Преобразование симметрии в пространстве. 4.Движение в пространстве. 5.Угол между прямой и плоскостью. 6.Угол между плоскостями. 7.Векторы в пространстве. 8.Площадь ортогональной проекции многоугольника. 9.Примеры.

1. Декартовы координаты в пространстве

Пусть заданы три взаимно перпендикулярные прямы x,y,z (Рис.1). Если провести через каждую пару прямых плоскость, то получим три взаимно перпендикулярные плоскости xy,xz,yz. Тогда прямые x,y,z будут называться осями координат, а точка пересечения О началом координат. Каждую ось точка О разбивает на две полуоси: положительную и отрицательную.

Возьмем теперь произвольную точку, например точку А. Тогда для того, чтобы определить координаты точки А, необходимо провести три плоскости, проходящие через точку А и параллельные плоскостям XY, XZ, YZ. Точки пересечения этих плоскостей с осями координат Аx, Ay, Az и будут являться координатами точки А, которые записываются так: А (Ax, Ay, Az).

Рис. 1 Декартовы координаты в пространстве.

2.Расстояние между двумя точками

Пусть задана декартова система координат с осями X, Y, Z (Рис.2). Необходимо найти расстояние между двумя точками А (x₁;y₁;z₁) и В (x₂;y₂;z₂).

Проведем два перпендикуляра от точек А и В на плоскость XY. Они пересекут плоскость XY в точках A’ и B’. Теперь проведем плоскость через точку А и параллельную плоскости XY. Тогда расстояние между точками по теореме Пифагора будет равно:

Таким образом, расстояние между двумя точками вычисляется по следующей формуле:

Рис.2 Расстояние между двумя точками

3. Преобразование симметрии в пространстве

Преобразование фигур в пространстве определяется таким же образом, как и преобразование фигур на плоскости (Рис.3). Помимо преобразования относительно точки и преобразования относительно прямой, в пространстве рассматривают преобразование относительно плоскости.

Пусть в пространстве задана плоскость α. В не этой плоскости задан квадрат со сторонами АВСD. Каждую точку нашей фигуры проецируем на плоскость α. А затем откладываем такое же расстояние по другую стороны плоскости и получаем преобразованную фигуру A»B»C»D». Таким образом, точки A»B»C»D» симметричны точкам ABCD относительно плоскости так же, как и все точки квадрата ABCD. Такое преобразование называется преобразованием относительно плоскости. А плоскость называется плоскостью симметрии. Если точка принадлежит плоскости α, то она переходит в саму себя.

Рис. 3 Преобразование симметрии в пространстве.

4. Движение в пространстве

Движение в пространстве определяется таким же образом, как и на плоскости. При движении в пространстве сохраняются расстояния между точками. И так же, как и на плоскости, прямые переходят в прямые, отрезки в отрезки, углы между полупрямыми сохраняются. Новым свойством, которым обладает движение в пространстве, являются то, что при движении плоскость переходит в плоскость.

Пусть задана плоскость α. Отметим на ней точки А,В,С не лежащие на одной прямой и построим на них треугольник (Рис.4). При движении эти точки передут в точки A’, B’, C’ также не лежащие на одной прямой. Проведем на плоскости α прямую, перескающую треугольник в точках X и Y и отметим на ней точку Z. При движении точки X и Y передут в точки X’ и Y’, прямая а передет в прямую a’. Следовательно она будет принадлежать плоскости α’. Таким образом, плоскость α переходит в плоскость α’. При движении фигур в пространстве, две фигуры называются равными, если они переходят сами в себя, т.е. совмещаются.

Рис. 4 Движение в пространстве.

Параллельный перенос

Парралельный перенос в пространстве задается формулами:

x’ = x + a
y’ = y + b
z’ = z + c

Подобие пространственных фигур

Преобразование подобия фигур в пространстве (гомотетия) определяется таким же образом, как и на плоскости. (Рис. 4.1)

При преобразования подобия расстояние между точками изменяется в одно и тоже число раз. Прямые переходят в прямые, полупрямые в полупрямые, отрезки в отрезки. Углы между полупрямыми сохраняются. При преобразовании подобия плоскость, не проходящая через центр гомотетии, переходит в параллельную плоскость. Так же, как и на плоскости преобразование подобия с коэффициентом гомотетии k переводит точки A и B в точки A’ и B’, отрезок АВ в отрезок A’B’ = k AB.

Рис. 4.1 Подобие пространственных фигур.

5. Угол между прямой и плоскостью

Пусть задана плоскость α. Прямая с пересекает плоскость α в точке А (Рис.5). Точка А лежит на прямой c’. Прямая c’ называется проекцией прямой с на плоскость α. Таким образом, углом между прямой и плоскостью является угол между прямой и ее проекцией на данную плоскость. Т.е. угол между прямой с и c’.

Рис. 5 Угол между прямой и плоскостью.

6. Угол между плоскостями

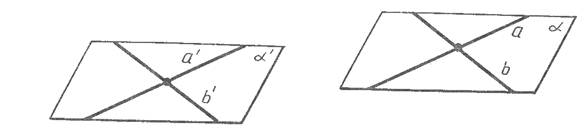
Пусть заданы две пересекающиеся плоскости α и β (Рис.6). Проведем плоскость γ, которая перпендикулярна их прямой пересечения с. Плоскость γ пересекает данные плоскости по прямым а и b. Угол между прямыми а и b и есть угол между данными плоскостями α и β.

Возьмем другую секущую плоскость γ’, которая параллельна γ и перпендикулярна прямой с. Она пересечет плоскости α и β по прямым a’ и b’. Если мы выполним параллельный перенос плоскости γ вдоль прямой с, то т.к. прямые а и a’ находятся в одной плоскости α и перпендикулярны прямой с, следовательно они совпадут. Таким образом, угол между плоскостями не зависит от секущей плоскости.

Рис. 6 Угол между плоскостями.

7. Векторы в пространстве

Действия над векторами

Действия над векторами в пространстве определяются так же, как и на плоскости.

Рис. 7 Векторы в пространстве.

8. Площадь ортогональной проекции многоугольника

Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью его проекции.

Если геометрическая фигура представляет собой многоугольник, то площадь ортогональной проекции можно найти, разбив его на простые треугольники, в которых хотя бы одна сторона будет параллельна плоскости проекции.

Рис. 8 Площадь ортогональной проекции многоугольника.

9. Пример 1

Докажите, что движение в пространстве переводит плоскость в плоскость.

Доказательство:

Пусть дана плоскость α. Проведем в плоскости α две пересекающиеся прямые a и b. Они пересекаются в точке О (Рис.9). Доказать, что при движении плоскость α переходит в плоскость α’.

Подвергнем две прямые а и b движению.Тогда они перейдут в прямые a’ и b’ с точкой пересечения O’. Угол ϕ между ними сохранится. Проведем через прямые a’ и b’ плоскость α’.

Если в плоскости α провести прямую с, то она пересечет прямые а и b в точках А и В. При движении прямая с перейдет в прямую с’. А точки А и В перейдут в точки A’ и B’.

Таким образом, две точки A’ и B’ принадлежат плоскости α’, так как прямая с’ пересекает прямые а’ и b’ в этих точках. А следовательно и вся прямая c’, т.е. все ее точки, принадлежат плоскости α’. Отсюда следует, что плоскость α переходит в плоскость α’.

Рис.9 Задача. Докажите, что движение в пространстве переводит плоскость в плоскость.

Пример 2

В плоскости xy найдите точку D (x; y; 0), равноудаленную от трех данных точек: А (1; 1; 1), В (1; 2; 2), С (2; 0; 1).

Решение:

Так как расстояние от точки D до точек А, В и С одинаковое, то можно составить следующие соотношения:

Приравняем первое и второе уравнения:

Теперь приравняем второе и третье уравнения:

Подставляя y = 3, получим х = 4 и D (4;3;0).

Рис.10 Задача. В плоскости xy найдите точку D (x; y; 0).

Пример 3

Докажите, что четырехугольник АВСD является параллелограммом, если: А (0; 2; 1), В (1; 1; 1), С (2; 2; 3), D (1; 3; 3).

Решение:

По свойству параллелограмма, его диагонали пересекаются в точке, которая делит их пополам. Следовательно, можно найти середины отрезков АС и BD:

x_AC = (2 + 0) / 2 = 1; y_AC = (2 + 2) / 2 = 2; z_AC = (1 + 3) / 2 = 2

x_BD = (1 + 1) / 2 = 1; y_BD = (1 + 3) / 2 = 2; z_BD = (3 + 1) / 2 = 2

Так как координаты середин отрезков АС и BD совпадают, то АВСD является параллелограммом (Рис. 11).

Рис.11 Задача. Докажите, что четырехугольник АВСD является параллелограммом.

Пример 4

Из точки, отстоящей от плоскости на расстоянии 4 м, проведены две наклонные, которые пересекают плоскость в точках А и В. Они образуют с плоскостью углы 45° и 30°, а между собой прямой угол. Найдите расстояние АВ между точками пересечения наклонных с плоскостью.

Решение:

Из прямоугольного треугольника СОВ (Рис.12) найдем СВ:

СВ = СО / sin 30° = 4 / 1 / 2 = 8 м.

Из прямоугольного треугольника СОА найдем СА:

АС = СО / sin 45° = 4 / 1 / = 4 м.

Теперь из прямоугольного треугольника АВС найдем АВ:

АВ 2 = 8 2 + (4) 2

АВ = 4 м.

Рис.12 Задача. Из точки, отстоящей от плоскости на расстоянии 4 м.

Пример 5

Через катет равнобедренного прямоугольного треугольника проведена плоскость под углом 45° ко второму катету. Найдите угол между гипотенузой и плоскостью.

Решение:

Из прямоугольного треугольника АВО найдем ВО (Рис.13):

ВО = АВ sin 45° = АВ /

Из прямоугольного треугольника АВС найдем ВС:

ВС 2 = AB 2 + AC 2 = 2 AB 2 (т.к. АВ = АС по условию задачи)

ВС = AB

Теперь из прямоугольного треугольника ВОС найдем синус угла ВСО:

sin ∠BCO = BO / BC = АВ / / AB = 1/2

Отсюда следует, что ∠ ВСО = 30°.

Рис.13 Задача. Через катет равнобедренного прямоугольного треугольника.

Источник

Движение переводит плоскость в плоскость

4. Движение переводит плоскость в плоскость.

Докажем, что при рассматриваемом движении плоскость a переходит в плоскость a’.

Итак прямая a’ лежит в плоскости a’. Точка X при движении переходит в точку X’ прямой a’, а значит, и плоскости a’, что и требовалось доказать.

В пространстве, так же как и на плоскости, две фигуры называются равными, если они совмещаются движением.

III. Виды движения: симметрия относительно точки, симметрия относительно прямой, симметрия относительно плоскости, поворот, движение, параллельный перенос.

Симметрия относительно точки

Преобразование фигуры F в фигуру F’, при котором каждая ее точка X переходит в точку X’, симметричную относительно данной точке O, называется преобразованием симметрии относительно точки O. При этом фигуры F и F’ называются симметричными относительно точки O.

Если преобразование симметрии относительно точки O переводит фигуру F в себя, то она называется центрально-симметричной, а точка O называется центром симметрии.

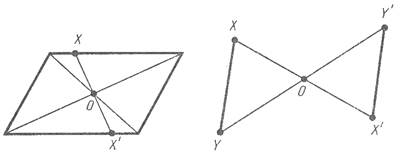
Например, параллелограмм является центрально-симметричной фигурой. Его центром симметрии является точка пересечения диагоналей.

Теорема: Преобразование симметрии относительно точки является движением.

Симметрия относительно прямой

Преобразование фигуры F в фигуру F’, при котором каждая ее точка X переходит в точку X’, симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g. При этом фигуры F и F’ называются симметричными относительно прямой g.

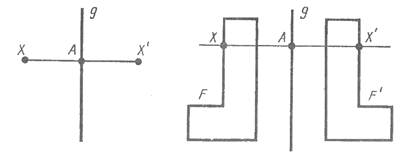
Если преобразование симметрии относительно прямой g переводит фигуру F в себя, то эта фигура называется симметричной относительно прямой g, а прямая g называется осью симметрии фигуры.

Например, прямые, проходящие через точку пересечения диагоналей прямоугольника параллельно его сторонам, является осями симметрии прямоугольника. Прямые на которых лежат диагонали ромба, является его осями симметрии.

Теорема: Преобразование симметрии относительно прямой является движением.

Возьмем две произвольные точки A (x;y) и B (x;y). Они перейдут в точки A’ (-x;y) и B’ (-x;y).

Отсюда видно, что AB=A’B’. А значит, что преобразование симметрии относительно прямой есть движение. Теорема доказана.

Симметрия относительно плоскости

Если точка X лежит в плоскости a, то считается, что точка X переходит в себя. Если преобразование симметрии относительно плоскости a переводит фигуру в себя, то фигура называется симметричной относительно плоскости a, а плоскость a называется плоскостью симметрии этой фигуры.

Поворот плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из точки, поворачивается на один и тот же угол в одном и том же направлении.
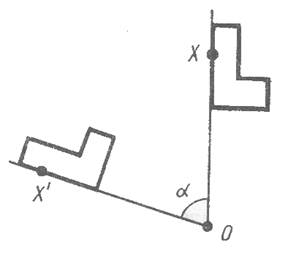
Это значит, что если при поворот около точки O точка переходит в точку X’, то лучи OX и OX’ образуют один и тот же угол, какова бы ни была точка X. Этот угол называется углом поворота. Преобразование фигур при повороте плоскости также называется поворотом.

Параллельный перенос в пространстве

Параллельным переносом в пространстве называется такое преобразование, при котором произвольная точка (x; y; z) фигуры переходит в точку (x+a; y+b; z+c), где числа a,b,c одни и те же для всех точек (x; y; z). Параллельный переносов пространстве задается формулами

выражающими координаты x’, y’, z’ точки, в которую переходит точка (x; y; z) при параллельном переносе. Так же, как и на плоскости, доказываются следующие свойства параллельного переноса:

1. Параллельные перенос есть движение.

2. При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.

3. При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).

4. Каковы бы ни были точки A и A’, существует единственный параллельный перенос, при котором точка A переходит в точку A’.

Новым для параллельного переноса в пространстве является следующее свойство:

5. При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную её плоскость.

Список использованной литературы:

1. Учебник Геометрии 7-11 классы. А.В. Погорелов

2. Учебник Геометрии 10-11 классы. А.Д. Александров.

Источник

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класс

Урок №4. Движения в пространстве

Перечень вопросов, рассматриваемых в теме:

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 121-126.

Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.

Потоскуев Е.В., Звавич Л. И., Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-63.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Определение движения в пространстве

Преобразованием пространства называется взаимно-однозначное отображение пространства на себя.

Два преобразования называются равными, если образы любой точки при этих преобразованиях совпадают.

Точка А называется неподвижной точкой при некотором преобразовании f, если при этом преобразовании она отображается на себя.

Фигура F называется неподвижной фигурой при некотором преобразовании f, если при этом преобразовании она отображается на себя.

Преобразование пространства, которое каждую точку отображает на себя, называется тождественным преобразованием. Оно обычно обозначается Е. При тождественном преобразовании все точки и все фигуры пространства являются неподвижными.

Для любых двух преобразований можно рассмотреть третье, которое получается последовательным применением этих преобразований. Например, если преобразование f отображает точку М на точку М’, а преобразование g отображает точку М’ на точку M», то преобразование f°g отображает точку М на точку M»: f°g(М)=g(f(M))=M».

Под движением пространства понимается отображение пространства на себя, при котором любые две точки A и B переходят (отображаются) в некие точки A₁ и B₁ так, что |AB|=|A₁B₁|.

Иными словами, движение пространства — это отображение пространства на себя, сохраняющее расстояния между точками. Так же, как и для движения на плоскости, можно доказать, что при движении в пространстве

— прямые переходят в прямые,

— полупрямые — в полупрямые,

— отрезки — в отрезки,

— сохраняются углы между прямыми.

Новое свойство движения в пространстве: движение переводит плоскости в плоскости.

В пространстве, так же как и на плоскости, две фигуры называются равными, если они совмещаются движением.

Можно доказать, что композиция двух движений пространства есть движение.

Центральная симметрия в пространстве задается и определяется так же, как и на плоскости

Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно точки O, называется центральной симметрией пространства относительно точки O. При этом точка O отображается на себя и называется центром симметрии.

Рисунок 1 – Центральная симметрия

На рисунке точка О – центр симметрии, АО=А₁О, ВО=В₁О, СО=С₁О, DО=D₁О (по определению точки, симметричной данной).

Центральная симметрия имеет только одну неподвижную точку – центр симметрии.

Сформулируем некоторые свойства центральной симметрии:

1) Прямая, проходящая через центр симметрии, отображается на себя.

2) Прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую.

3) Плоскость, проходящая через центр симметрии, отображается на себя (то есть является неподвижной плоскостью этой центральной симметрии).

4) Плоскость, не проходящая через центр симметрии, отображается на параллельную ей плоскость.

3. Осевая симметрия (симметрия относительно прямой):

Точка M’ пространства, не лежащая на прямой m, называется симметричной точке М относительно прямой m, если отрезок ММ’ перпендикулярен этой прямой и делится ею пополам.

Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно прямой m, называется осевой симметрией пространства относительно прямой m. Прямая m отображается на себя и называется осью симметрии.

Рисунок 2 – Осевая симметрия

Неподвижные прямые осевой симметрии:

2) любая прямая, перпендикулярная прямой m

Неподвижные плоскости осевой симметрии:

1) любая плоскость, проходящая через прямую m

2) любая плоскость, перпендикулярная прямой m.

Зеркальная симметрия (симметрия относительно плоскости):

Точка M’ пространства, не лежащая на плоскости α, называется симметричной точке М относительно плоскости α, если отрезок ММ’ перпендикулярен этой плоскости и делится ею пополам.

Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости α, называется зеркальной симметрией пространства относительно плоскости α. Плоскость α отображается на себя и называется плоскостью симметрии.

Рисунок 3 – Зеркальная симметрия

Неподвижные прямые зеркальной симметрии:

1) любая прямая плоскости α

2) любая прямая, перпендикулярная плоскости α

Неподвижные плоскости зеркальной симметрии:

1) сама плоскость α

2) любая плоскость, перпендикулярная плоскости α.

Параллельный перенос (точки переносятся на данный вектор):

Рисунок 4 – параллельный перенос

Пусть дан вектор .

Преобразование пространства, при котором каждая точка пространства M, отображается на такую точку M’, что выполняется равенство , называется параллельным переносом на вектор .

Перенос на нулевой вектор является тождественным преобразованием.

Параллельный перенос отображает прямую на параллельную ей прямую либо на себя; плоскость на параллельную ей плоскость либо на себя.

Неподвижных точек параллельный перенос на ненулевой вектор не имеет.

Неподвижными прямыми при параллельном переносе на вектор являются прямые, параллельные этому вектору.

Неподвижными плоскостями при параллельном переносе на вектор являются плоскости, параллельные этому вектору.

Поворот на данный угол вокруг данной оси:

Поворотом пространства на угол φ вокруг прямой n называется такое преобразование пространства, при котором любая точка прямой остается неподвижной и в любой плоскости, перпендикулярной прямой n, осуществляется поворот этой плоскости на угол φ вокруг точки ее пересечения с прямой n.

Рисунок 5 – Поворот вокруг прямой

Неподвижными точками являются любая точка оси вращения.

Неподвижной прямой является ось поворота.

Неподвижной плоскостью является любая плоскость, перпендикулярная оси поворота.

Поворот вокруг оси на угол 180 0 является осевой симметрией.

Примеры и разбор решения заданий тренировочного модуля

Дан треугольника АВС: А(3,- 2, 4), В (4, 6, 0), С (2, 2, 2)

В какую точку перейдет центр О пересечения медиан данного треугольника при:

Симметрия относительно начала координат

Симметрия относительно координатной плоскости ZOY

Поворот на угол 180 0 относительно координатной оси OZ

Симметрия относительно плоскости х=2

Найдем точку пересечения медиант данного треугольника.

М (); М(3; 4; 1)

Так как медианы треугольника пересекаются в одной точке и делятся в отношении 2:1, считая от вершины, то можем найти координаты точки О, зная координаты А и М:

Теперь найдем координаты образа точки О при каждом из преобразований:.

. То есть координаты образа: (5; 0; 5)

(ордината и аппликата точки остаются такими же, а абсцисса меняет знак). То есть координаты образа: (-3; 2; 2).

Эта плоскость параллельная плоскости ZOY, поэтому ордината и аппликата точки остаются такими же. Так как абсцисса токи О х_о =3, то расстояние от точки до плоскости α равно 1. Точка, симметричная точке О относительно плоскости α, будет иметь абсциссу, равную х_о’ =1.

Источник