Докажите что если две параллельные плоскости пересекаются третьей то прямые пересечения параллельны
Если две параллельные плоскости пересекаются третьей, то линии их пересечения параллельны
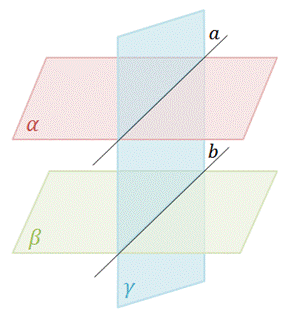
Доказательство. Пусть аир — параллельные плоскости, у — секущая плоскость, а и Ь — линии пересечения (рис. 16). Докажем, что прямые а и Ъ параллельны.
 |
Предположим, что а и Ъ не параллельны. Тогда, так как они лежат в одной плоскости у, то пересекутся в некоторой точке Р. Точка Р принадлежит прямым а и Ъ и, значит, является общей точкой плоскостей аир. Но это противоречит тому, что плоскости а и Р параллельны. Итак,
 |
прямые а и & не пересекаются. Значит, они параллельны. Теорема доказана.
Теорема 10. Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны.
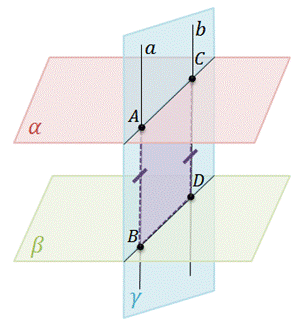
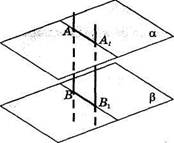
Доказательство. Пусть отрезки АВ и А1В1 параллельны, а их концы лежат в параллельных плоскостях а и р (рис. 17). Третья плоскость, проходящая через прямые АВ и AXBV пересекает параллельные плоскости аир по параллельным прямым: (AAJ || (BBJ. Кроме того, по условию теоремы (АВ) || (AjSj). Значит, четырехугольник АВВ1А1 — параллелограмм. Следовательно, \АВ\ = \АХВ^. Теорема доказана.
Теорема 11. Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.
 |
 |
| Рис.18 |
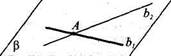
Доказательство. Пусть а — плоскость, А — не лежащая на ней точка. Чтобы через данную точку А провести плоскость р, параллельную плоскости а, сначала в плоскости а проведем какие-нибудь две пересекающиеся прямые ах и а2 (рис.18). Потом через данную точку А проведем параллельные им прямые &х и Ь2. Прямые &х и Ъ2 определяют единственную плоскость р (теорема 2). А по следствию теоремы 8 Pilot. Единственность такой плоскости Р не вызывает сомнений.
Следствие. Две плоскости, параллельные третьей плоскости, параллельны.
Следствие легко доказывается с помощью теоремы 11. Если даны три плоскости а, р, у, такие, что а || у, Р || у, то ясно, что Р || а. Действительно, если предположим, что а п р = Ъ (прямая), то через некоторую точку А прямой Ъ проходили бы две плоскости, параллельные плоскости у. А это противоречит теореме 11. Поэтому а || р.
Вопросы и задания
1.Какие плоскости называются параллельными?
2. Докажите теорему о признаке параллельности двух плоскостей.
3. Докажите, что если две параллельные плоскости пересекаются третьей, то
прямые пересечения параллельны.
4. Докажите, что отрезки параллельных прямых, заключенные между двумя
параллельными плоскостями, равны.
5. Докажите, что через точку вне данной плоскости можно провести плоскость,
параллельную данной, и притом только одну.
6. Повторите и запомните следствия теорем.
7. В окружающей вас обстановке найдите примеры параллельных плоскостей,
плоскости и параллельной ей прямой.
 |
| Рис. 19 |
49.Две прямые плоскости а параллельны плоскости р. Следует ли
отсюда, что а || р?
50.а || р. Докажите, что каждая прямая плоскости а параллельна
плоскости р.
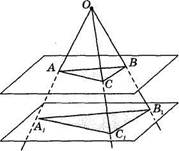
51.Отрезки О А, ОВ и ОС не лежат в одной плоскости. Докажите,
что плоскость, проходящая через их середины, параллельна плос
кости ABC.
52.Могут ли быть равными отрез
ки не параллельных прямых,
заключенные между двумя
параллельными прямыми?
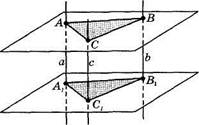
53.Через вершины треугольни
ка ABC, лежащего в одной из
двух параллельных плоскос
тей, проведены параллельные
прямые, пересекающие вторую
плоскость в точках AVBVCV
Докажите равенство треуголь
ников ABC и А1В1С1 (рис.19).
54. Две параллельные плоскости аир пересекают сторону АВ тре
угольника ABC в точках D и Dx, а сторону ВС соответственно в
точках Е и Ех Найдите длину отрезка DE, если \BD\ = 12 см,
\BDX\ = 18 см, l-Dj-EJ = 54 см.
55. Плоскость у пересекает плоскости а и р по параллельным пря
мым. Следует ли из этого, что плоскости аир параллельны?
56. Плоскости аир пересекаются. Докажите, что любая плоскость
пространства пересекает хотя бы одну из плоскостей а, р.
Через вершины параллелограмма ABCD, лежащего в одной из
двух параллельных плоскостей, проведены параллельные прямые,
пересекающие вторую плоскость в точках A1,B1,C1,D1. Докажите,
что четырехугольник A1,B1,C1,D1 тоже параллелограмм.
 |
58. Прямая а параллельна плоскости а.
Как через прямую а провести плос
кость, параллельную а?
59. Три прямые, проходящие через
одну точку, пересекают данную
плоскость в точках А, В, С, а парал
лельную ей плоскость в точках Av Bv
Cv Докажите подобие треугольников
ABC и A^q (рис. 20).
60. ABCDEFA — не плоская
Рис. 20
замкнутая ломаная из шести звеньев.
Докажите, что если [АВ] || [DE], [ВС] \\ [EF] и [CD] || [FA], то \АВ\ = \DE\, \ВС\ = \EF\ и |СД = \FA\. 61. Докажите, что если прямая пересекает одну из двух параллельных плоскостей, то пересекает и другую.
Свойства параллельных плоскостей
Урок 11. Геометрия 10 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Свойства параллельных плоскостей»
Для начала давайте вспомним определение параллельных плоскостей и признак параллельности двух плоскостей. Итак, две плоскости называются параллельными, если они не пересекаются. Признак параллельности плоскостей:если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
А теперь рассмотрим свойства параллельных плоскостей.
Первое свойство.Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Доказательство. Пусть даны параллельные плоскости α и β. И пусть дана плоскость γ, которая пересекает плоскости α и β по прямым а и b соответственно. Докажем, что прямая а параллельна прямой b.
Рассмотрим прямые а и b. Действительно, эти прямые лежат в одной плоскости γ и не пересекаются. Если бы прямые а и bпересекались, то их общая точка принадлежала бы плоскостям α и β, чего быть не может, так как по условию они параллельны.
Таким образом, прямые а и b лежат в одной плоскости и не пересекаются, т.е. прямая а параллельна прямой b.Что и требовалось доказать.
Наглядным представлением данного свойства служат линии пересечения пола и потолка со стеной комнаты – эти линии параллельны.
Второе свойство.Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Доказательство.Пусть даны параллельные плоскости α и β. И пустьданы параллельные отрезкиAB и CD, которыележат на параллельных прямых а и b, расположенных между плоскостями α и β. Докажем, что отрезок ABравен отрезку CD.
Две параллельные прямые а и b образуют единственную плоскость γ. Плоскость γ, проходящая через параллельные прямые а и b, пересекает плоскости α и β по прямымAC и BD. По первому свойству, если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны, следует, что прямыеAC и BD – параллельны. А, значит, четырехугольник ABDC – параллелограмм, так как в нем противолежащие стороны попарно параллельны. По свойству противоположных сторон параллелограмма, следует, чтоотрезок AB равен отрезкуCD.Что и требовалось доказать.
Третье свойство.Через точку, не лежащую в данной плоскости, проходит плоскость, параллельная данной, и притом единственная.
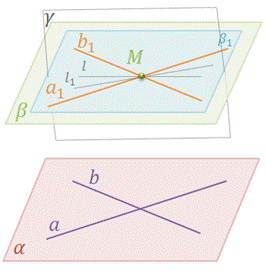
Доказательство. Пусть дана плоскость α и точка M, которая не лежит в данной плоскости. Проведем в плоскости α две пересекающиеся прямые а и b. Через точку M проведем прямые а1 и b1, параллельные прямым а и b соответственно.
Рассмотрим плоскость β, проходящую через прямые а1 и b1. Плоскость β – искомая, так как она проходит через точку M и по признаку параллельности двух плоскостей параллельна плоскости α.
Докажем единственность плоскости β. Предположим, что существует другая плоскость β1, которая проходящая через точку M и параллельна плоскости α.
Плоскость γ, проходящая через точку М и прямую а, пересекает плоскости β и β1, так как с каждой из них плоскость гамма имеет общую точку М.
Следовательно, линии пересеченияl и l1 плоскости гамма с плоскостями β и β1, проходят через точку М и параллельны прямой а. Получили, что через точку М, не лежащую на прямой а, проходят две прямые, параллельные прямой а. А это противоречит теореме о том, что через точкуМ, не лежащей на прямой а, можно провести единственную прямую, параллельную данной. Значит, наше предположение неверно и плоскость β единственная. Что и требовалось доказать.
Задача. Даны плоскости 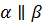
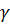
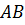
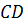
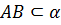
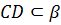
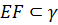
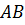
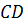
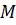
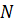
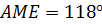
Ответ: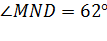
Подведем итоги урока. На этом уроке мы рассмотрели некоторые из свойств, которыми обладают две параллельные плоскости в пространстве. Узнали, что если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Доказали, что отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. А также доказали свойство о существовании единственнойплоскости, параллельной данной плоскости и проходящей через точку вне ее.
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок №6. Параллельность плоскостей
Перечень вопросов, рассматриваемых в теме
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Определение. Плоскости, которые не пересекаются, называются параллельными.
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии 10 Москва «Просвещение» 2013 год. С. 1-4.
Зив Б. Г. Геометрия 10 класс Дидактические материалы Москва «Просвещение» 2013 год. С.4, 14, 24
Теоретический материал для самостоятельного изучения
Как известно из аксиом стереометрии, если плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Значит две плоскости или пересекаются, или не пересекаются.
Определение. Плоскости, которые не пересекаются, называются параллельными.
Параллельные плоскости α и β обозначаются α∥β.

Допустим, что плоскости α и β не параллельны, то есть они пересекаются по некоторой прямой c.
Прямая a1 параллельна прямой b1, значит она параллельна и самой плоскости β.
Прямая a2 параллельна прямой b2, значит она параллельна и самой плоскости β (признак параллельности прямой и плоскости).
Прямая c принадлежит плоскости α, значит хотя бы одна из прямых a1 или a2 пересекает прямую c, то есть имеет с ней общую точку. Но прямая c также принадлежит и плоскости β, значит, пересекая прямую c, прямая a1 или a2 пересекает плоскость β, чего быть не может, так как прямые a1 и a2 параллельны плоскости β.
Из этого следует, что плоскости α и β не пересекаются, то есть они параллельны.
Свойства параллельных плоскостей.

Плоскость α пересекается с плоскостью γ по прямой a.
Плоскость β пересекается с плоскостью γ по прямой b.
Линии пересечения a и b лежат в одной плоскости γ и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.

Проведённая плоскость пересекается с плоскостью α по прямой AB, а с плоскостью β по прямой CD.
По предыдущей теореме прямые AB и CD параллельны. Четырехугольник ABCD есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть BC=AD.
Теорема 3. Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую.
Пусть α||β, a пересекает α в точке А.
Выберем в плоскости любую точку C. Через эту точку и прямую a проведём плоскость.
Так как плоскость имеет с плоскостями α и β общие точки A и C соответственно, то она пересекает эти плоскости по некоторым прямым b и c, которые проходят соответственно через точки A и C. По предыдущей теореме прямые b и c параллельны. Тогда в плоскости прямая a пересекает (в точке A) прямую b, которая параллельна прямой c. Значит, прямая a пересекает и прямую c в некоторой точке B. Так как прямая c лежит в плоскости, то точка B является точкой пересечения прямой a и плоскости. Теорема доказана.

Пусть α||β, α и γ пересекаются.
Докажем, что плоскости β и γ пересекаются.
Проведём в плоскости γ прямую a, пересекающую плоскость α в некоторой точке B. Тогда по теореме 3 прямая a пересекает и плоскость β в некоторой точке A. Следовательно, плоскости β и γ имеют общую точку A, т. е. пересекаются. Теорема доказана.
Теорема 5. Через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и притом только одну.
Пусть нам даны плоскость α и точка М, ей не принадлежащая.
Докажем, что существует плоскость β, которой принадлежит точка М, параллельная плоскости α.

Докажем методом от противного, что β — единственная плоскость, удовлетворяющая условию теоремы.
Допустим, что через точку M проходит другая плоскость, например β1, параллельная α.
Так как β1 пересекает плоскость β (они имеют общую точку M), то по теореме 4 плоскость β1 пересекает и плоскость α (β ‖ α). Мы пришли к противоречию. Таким образом, предположение о том, что через точку M можно провести плоскость, отличную от плоскости β и параллельную плоскости α, неверно. Значит, плоскость β — единственна. Теорема доказана.
Рассмотрим несколько примеров на применение данных свойств.
Даны две пересекающиеся прямые a и b точка А, не лежащая в плоскости этих прямых. Докажите, что через точку А проходит плоскость, параллельная прямым a и b, и притом только одна.
Прямые a и b пересекаются по условию, следовательно, по следствию из аксиомы А1, эти прямые единственным образом определяют плоскость α.
Известно, что через точку А, не принадлежащую плоскости α, проходит единственная плоскость, параллельная α, т.е. параллельная прямым a и b (по теореме 5) .
Плоскости α и β параллельны, прямая m лежит в плоскости α. Докажите, что прямая m параллельна плоскости β.
Предположим, что прямая m пересекает плоскость β в точке М. Тогда точка М принадлежит плоскости α (т.к. прямая m лежит в плоскости α) и М принадлежит плоскости β, значит, α и β пересекаются, но они параллельны по условию. Очевидно, m не пересекает плоскость α, т.е. параллельна ей.
Примеры и разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Рассмотрим плоскость, проходящую через прямые А1А2 и В1В2
(она существует и единственная, т.к. прямые пересекаются).
В этой плоскости лежит четырехугольник А1В1А2В2, диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А1В1 и А2В2 параллельны.
Аналогично доказывается параллельность В1С1 и В2С2. Из вышеперечисленного следует, что плоскости А1В1С1 и А2В2С2 параллельны по признаку параллельности плоскостей.
Рассмотрим плоскость, проходящую через прямые А1А2 и В1В2
(она существует и единственная, т.к. прямые пересекаются).
В этой плоскости лежит четырехугольник А1В1А2В2, диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А1В1 и А2В2 параллельны.
Аналогично доказывается параллельность В1С1 и В2С2. Из вышеперечисленного следует, что плоскости А1В1С1 и А2В2С2 параллельны по признаку параллельности плоскостей.
Тип задания: выделение цветом
Два равнобедренных треугольника FKС и FKD с общим основанием FK расположены так, что точка С не лежит в плоскости FKD. Определите взаимное расположение прямых, содержащих медианы треугольников, проведенных к сторонам KС и KD.
Прямые, которые содержат медианы треугольников к KC и KD- выходят из одной точки F. Соответственно, можно сделать вывод, что данные прямые пересекаются.