Докажите что если две параллельные прямые пересечены секущей то соответственные углы равны

Теорема о равенстве соответственных углов. Теорема о свойстве односторонних углов

Урок 18. Геометрия 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Теорема о равенстве соответственных углов. Теорема о свойстве односторонних углов»

Вспомним теорему о равенстве накрест лежащих углов:

Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

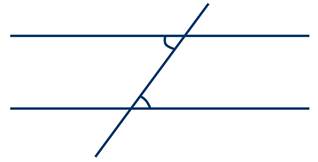
Если две параллельные прямые пересечены секущей, то соответственные углы равны.

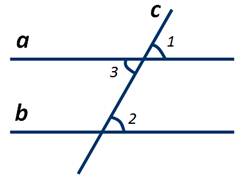
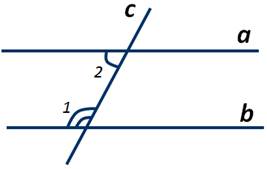
Пусть параллельные прямые а и b пересечены секущей c. Необходимо доказать, что соответственные углы 1 и 2 равны. Так как прямая а параллельна прямой b, то накрест лежащие углы 2 и 3 равны. ∠1 и ∠3 равны как вертикальные. Из равенств ∠2=∠3 и ∠1=∠3 следует, что ∠1=∠2. Теорема доказана.

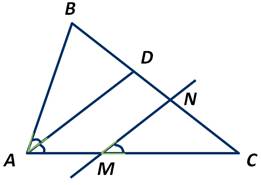
Пусть прямая MN параллельная биссектрисе AD треугольника АВС.

Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 градусов.

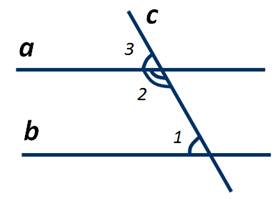
Пусть параллельные прямые а и b пересечены секущей c. Доказать, ∠1+∠2=180 градусов. Так как прямая а параллельна прямой b, то соответственные ∠1 и ∠3 равны. ∠2+∠3=180 градусов, так как углы 2 и 3 смежные. Тогда, из равенств угол ∠1=∠3 и ∠2+∠3=180 градусов, следует, что ∠1+∠2=180 градусов. Теорема доказана.

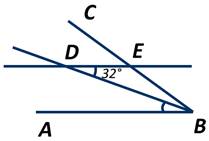
Например: пусть прямая DE параллельна стороне АВ треугольника АВС. Тогда ∠BAD+∠ADE=180 градусов.

Углы АВС и CED являются соответственными углами при параллельных прямых АВ и DE и секущей ВС, а значит, они равны. Следовательно, ∠CED=64 градуса.

Градусная мера одного из внутренних односторонних углов, образованных при пересечении двух параллельных прямых секущей, меньше градусной меры другого на 26 градусов. Вычислить градусные меры этих углов.

Пусть ∠1=x, тогда ∠2=x-26. Так как ∠1 и ∠2 являются внутренними односторонними при параллельных прямых а и b и секущей с, то их сумма равна 180 градусов, то есть ∠1+∠2=180 градусов.

Источник

Соответственные углы

Соответственные углы — вид углов, образованный при пересечении двух прямых секущей.

Один из пары соответственных углов лежит во внутренней области между прямыми, другой — во внешней, причем оба угла находятся по одну сторону от секущей.

При пересечении двух прямых секущей образуется четыре пары соответственных углов.

∠1 и ∠5

∠2 и ∠6

∠3 и∠7

∠4 и ∠8

— соответственные углы при прямых a и b и секущей c.

Наибольший интерес в геометрии представляют соответственные углы при параллельных прямых.

Свойство параллельных прямых

Если две параллельные прямые пересечены третьей прямой, то соответственные углы равны.

∠1 = ∠2

(как соответственные углы при при a ∥ b и секущей c).

Всего при параллельных прямых и секущей образуется четыре пары равных соответственных углов:

∠1 = ∠5

∠2 = ∠6

∠3 = ∠7

Признак параллельных прямых

Если соответственные углы равны, то прямые параллельны.

∠1 = ∠2

А так как эти углы — соответственные при прямых при a и b и секущей c,

то a ∥ b (по признаку параллельных прямых).

Равенство соответственных углов используется, в частности, для доказательства равенства треугольников и подобия треугольников.

Источник

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы

Углы и — вертикальные. Очевидно, вертикальные углы равны, то есть

Соответственные углы равны, то есть

Накрест лежащие углы равны, то есть

Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.

Ты нашел то, что искал? Поделись с друзьями!

Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.

Периметр параллелограмма — это сумма всех его сторон, то есть

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Углы и — односторонние при параллельных прямых и секущей, следовательно,

Источник