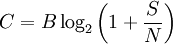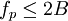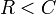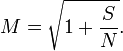Докажите что формула хартли является частным случаем формулы шеннона
Теорема Шеннона-Хартли
Теорема Шеннона-Хартли
Теорема Шеннона-Хартли в теории информации — применение теоремы кодирования канала с шумом к архетипичному случаю непрерывного временного аналогового канала коммуникаций, искаженного гауссовским шумом. Теорема устанавливает шенноновскую ёмкость канала, верхнюю границу максимального количества безошибочных цифровых данных (то есть, информации), которое может быть передано по такой связи коммуникации с указанным полоса пропускания в присутствии шумового вмешательства, согласно предположению, что мощность сигнала ограничена, и Гауссовский шум характеризуется известной мощностью или мощностью спектральной плотности. Закон назван в честь Клода Шеннона и Ральфа Хартли.
Содержание
Утверждение теоремы
Рассматривая все возможные многоуровневые и многофазные методы шифрования, теорема Шеннона-Хартли утверждает, что ёмкость канала C, означающая теоретическую верхнюю границу скорости передачи данных, которые можно передать с данной средней мощностью сигнала S через аналоговый канал связи, подверженный аддитивному белому гауссовскому шуму мощности N равна:
C — ёмкость канала в битах в секунду; B — полоса пропускания канала в герцах; S — полная мощность сигнала над полосой пропускания, измеренной в ваттах или вольтах в квадрате; N — полная шумовая мощность над полосой пропускания, измеренной в ваттах или вольтах в квадрате; S/N — отношение сигнала к шуму(SNR) сигнала к гауссовскому шуму, выраженное как отношение мощностей.
История развития
В течение конца 1920-ых Гарри Найквист и Ральф Хартли разработали фундаментальные идеи, связанные с передачей информации, с помощью телеграфа как система коммуникаций. В то время, это был прорыв, но науки как таковой не существовало. В 1940-ых, Клод Шеннон ввел понятие способности канала, которое базировалось на идеях Найквиста и Хартли, а затем сформулировал полную теорию передачи информации.
Критерий Найквиста
Формула Хартли
Теоремы Шеннона для канала с шумами
Теоремы Шеннона для канала с шумами (теоремы Шеннона для передачи по каналу с шумами) связывают пропускную способность канала передачи информации и существование кода, который возможно использовать для передачи информации по каналу с ошибкой, стремящейся к нулю (при увеличении длины блока).
Если скорость передачи сообщений меньше пропускной способности канала связи,
то существуют коды и методы декодирования такие, что средняя и максимальная вероятности ошибки декодирования стремятся к нулю, когда длина блока стремится к бесконечности,
C \,» style=»max-width : 98%; height: auto; width: auto;» src=»http://dic.academic.ru/pictures/wiki/files/48/06361f1e73691ae593c595b5dc19371f.png» border=»0″ />
то тогда, на основе которого можно добиться сколько угодной малой вероятности возникновения ошибки, не существует.
Теорема Шеннона-Хартли
В данной теореме определено, что достичь максимальной скорости (бит/сек) можно путем увеличения полосы пропускания и мощности сигнала и, в то же время, уменьшения шума.
Теорема Шеннона-Хартли ограничивает информационную скорость (бит/с) для заданной полосы пропускания и отношения сигнал/шум. Для увеличения скорости необходимо увеличить уровень полезного сигнала, по отношению к уровню шума.
Значение теоремы
Сравнение способности Шеннона к законному Сравнению Хартли
способности канала к информационной норме из закона Хартли, мы можем найти эффективное число различимых уровней
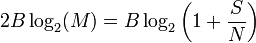
квадратный корень эффективно преобразовывает отношение мощности в отношение напряжения, таким образом число уровней приблизительно пропорционально отношению среднеквадратической амплитуды сигнала к шумовому стандартному отклонению. Это подобие в форме между способностью Шаннона и законом Hartley’s не должно интерпретироваться, чтобы означать, что М. уровней пульса можно буквально послать без любого беспорядка; больше уровней необходимо, чтобы учесть избыточное кодирование и устранение ошибки, но чистая скорость передачи данных, к которой можно приблизиться с кодированием, эквивалентна использованию того М. в законе Хартли.
Основы теории информации. Формула Хартли. Формула Шеннона.
Информация – это одно из фундаментальных понятий современной науки, наряду с понятиями материи и энергии. По-видимому, не только понятие. В начале прошлого века Эйнштейн показал, что материя и энергия – по сути одно и то же (знаменитая формула \(E=m c^2\) ). Современные исследования в физике указывают на то, что подобная связь может быть и между информацией и энергией.
С точки зрения же человека, информация – это некие сведения, которые могут быть понятными, достоверными, актуальными и т.п., или наоборот.
Существуют различные формальные подходы к определению информации. С точки зрения информатики, нас интересуют два определения.
Информация по Шеннону Информация – это снятая неопределенность.
Это удобное интуитивное определение. Неопределенность в данном случае – характеристика нашего незнания о предмете. Например, в момент броска игрального кубика, мы не знаем, какая из 6 граней выпадет. Когда же кубик останавливается на какой-то грани – мы получаем информацию.
Это определение, однако, не слишком удобно без некоторой количественной меры неопределенности.
Величина неопределенности количество возможных равновероятных исходов события
Так, например, игральный кубик имеет неопределенность 6.
Такой подход к определению информации называется содержательным. Он интуитивно понятен, однако, не отвечает на вопрос “сколько информации получено”.
Количество информации по Колмогорову количество информации, содержащееся в сообщении, записанном в виде последовательности символов, определяется минимально возможным количеством двоичных знаков, необходимых для кодирования этого сообщения, безотносительно к его содержанию.
Поскольку любой алфавит может быть закодирован в двоичном, очевидно это определение достаточно универсально: оно применимо для любого сообщения, которое может быть записано на каком-либо языке. Этот подход называется алфавитным.
В качестве основной единицы количества информации принято брать бит – от binary digit.
При алфавитном подходе один бит – это количество информации, которое можно закодировать одним двоичным знаком (0 или 1). С точки зрения содержательного подхода, один бит – это количество информации, уменьшающее неопределенность в два раза.
Существуют более крупные единицы информации, которые чаще используются на практике.
| название | размер |
|---|---|
| байт | 8 бит |
| килобайт | \(10^3\) байт |
| мегабайт | \(10^6\) байт |
| гигабайт | \(10^9\) байт |
| терабайт | \(10^<12>\) байт |
| кибибайт | \(2^<10>\) байт |
| мебибайт | \(2^<20>\) байт |
| гибибайт | \(2^<30>\) байт |
| тебибайт | \(2^<40>\) байт |
В вопросе хранения информации, основным показателем является не количество информации, а информационный объем
Информационный объем сообщения количество двоичных символов, используемых для кодирования сообщения.
В отличие от количества информации, информационный объем может быть не минимальным. В частности, кодирование текстов в различных кодировках далеко не оптимально.
Формула Хартли
Сколько же информации получается в результате броска кубика?
Рассмотрим сначала более простую задачу: сколько информации получается в результате броска монеты? Считаем, что возможны два варианта: “орел” и “решка”.
Исходя из содержательного подхода, неопределенность броска монеты составляет 2. После броска, мы имеем один вариант. Следовательно, неопределенность уменьшилась вдвое. В результате броска монеты мы получаем один бит информации.
Рассмотрим теперь бросок двух монет (или два броска одной монеты). Каждый из бросков имеет два варианта исхода. Всего мы имеем четыре варианта исхода: орел-орел, орел-решка, решка-орел, решка-решка. После бросков, мы получаем один конкретный вариант, то есть, неопределенность уменьшается в 4 раза – или дважды уменьшается в 2 раза. Мы, таким образом, получаем 2 бита информации.
Для броска трех монет, имеем 8 вариантов исхода, и в результате получаем 3 бита информации.
для набора из \(N\) различных символов можно составить \(N^m\) различных комбинаций (“слов”) длины \(m\) (это утверждение легко доказывается по индукции, и известно из комбинаторики).
Тогда при оптимальном кодировании информации (которое при неограниченном \(m\) достижимо с произвольной точностью), на один символ приходится \(\log_2 N\) бит информации (или, что то же, один символ кодируется в среднем \(\log_2 N\) двоичными символами) \(\blacksquare\)
Применения формулы Хартли
Формула Хартли находит много различных применений. Одно из наиболее интересных заключается в оценке классов сложности вычислительных задач. Рассмотрим на примере алгоритмов сортировки.
С точки зрения теории информации, сортировка представляет собой выбор из всех возможных перестановок массива одной такой, которая удовлетворяет критерию сортировки.
Массив длинны \(N\) имеет \(N!\) различных перестановок (это утверждение легко доказывается по индукции, и известно из комбинаторики).
Для больших \(N\) можно использовать формулу Стирлинга для оценки факториала: \[N! = \sqrt <2\pi N>N^N e^<-N>.\]
Таким образом, в частности, алгоритм сортировки слиянием по порядку роста близок к теоретически оптимальному.
Закон аддитивности информации
Еще одно занимательное следствие формулы Хартли – это аддитивность информации.
По формуле Хартли, количество информации, соответствующее выбору \((x_1, x_2)\) из \(X\) равно \[H(x_1, x_2) = \log_2(N_1 N_2)\]
По правилом арифметики с логарифмами,
\[\begin
Таким образом, по формуле Хартли, \[H(x_1, x_2) = H(x_1) + H(x_2),\] то есть, информация аддитивна – если мы получаем \(H_1\) информации об одном предмете и \(H_2\) – о другом, то всего мы получаем \(H_1 + H_2\) информации о двух предметах.
Закон аддитивности информации количество информации, необходимое для установления пары равно суммарному количеству информации, необходимому для независимого установления элементов пары.
Этот закон легко обобщается для набора \(N\) элементов.
Формула Шеннона
До сих пор мы рассматривали случай, когда все варианты равновероятны. Предположим, что это не так.
Рассмотрим новый алфавит \(
Тогда среднее количество информации на один символ сообщения
\[ H = P_a \log_2\frac<1>
Это частный случай формулы Шеннона – для двух-символьного алфавита.
Интересным оказывается то, что количество информации на один символ алфавита зависит от вероятности обнаружить этот символ.
\[ H(P_a) = P_a \log_2\frac<1>
График этой функции показан на рисунке:
Можно так же рассчитать производную:
Получается, что количество информации, получаемое в результате выбора одного элемента из двух, максимально при равных вероятностях и составляет 1 бит.
В других случаях, выбор из двух вариантов соответствует менее чем одному биту информации.
Действительно, база индукции для случая \(N=2\) уже доказана. Предположив, что формула верна для алфавита \(N-1\) элементов, вычислим \(H\) для \(N\) элементов.
Для этого, отождествим последние два символа алфавита. Для отождествленного алфавита количество информации на символ \[ H_
Среди двух отождествленных символов, каждый из них появляется с относительной вероятностью, соответственно, \[q_
Связь формул Хартли и Шеннона
Формула Хартли представляет собой частный случай формулы Шеннона.
Мы получили формулу Хартли.
Оптимальное кодирование информации
Для достижения соответствия информационного объема и количества информации, необходимо оптимальное кодирование информации.
Легко можно показать случаи не оптимального кодирования информации. Допустим, кодируется результат падения монеты: орел или решка. Мы уже знаем, что количество информации в данном случае равно одному биту. При этом, если закодировать эти значения, например, русскими словами в коде UTF-8, то в среднем на одно значение уйдет 9 бит.
Одним из достаточно эффективных и при этом универсальных алгоритмов является алгоритм кодирования Хаффмана.
Алгоритм Хаффмана
Алгоритм Хаффмана является алгоритмом префиксного кодирования: символы произвольного алфавита кодируются двоичными последовательностями различной длины таким образом, что ни один более короткий код не является префиксом более длинного. При этом, для достижения оптимального кодирования, наиболее часто встречающиеся символы кодируются наиболее короткой последовательностью, а наиболее редко встречающиеся – наиболее длинной.
Для построения кода, всем символам алфавита присваиваются значения приоритетов, соответствующие частоте появления символа.
Затем два символа с наименьшим значением приоритета “склеиваются”, образуя при этом бинарное дерево (выбор символов с одинаковым приоритетом произволен). Результат получает приоритет, равный сумме приоритетов входящих в него символов. Процесс продолжается, пока в итоге не останется одно бинарное дерево.
После этого, “левым” ветвям дерева (с более низким приоритетом) присваивается код “0”, а “правым” (с более высоким) – “1”. Кодом символа является последовательность кодов ветвей, приводящих к нему.
Например, нам нужно оптимально закодировать сообщение “шла Маша по шоссе”. Всего сообщение состоит из 17 символов. Символы алфавита и их приоритеты:
| Символ | Приоритет |
|---|---|
| » « | 4 |
| “ш” | 3 |
| “a” | 2 |
| “о” | 2 |
| “с” | 2 |
| “л” | 1 |
| “M” | 1 |
| “п” | 1 |
| “е” | 1 |
“Склеим” символы “п”, “е”:
| Символ | Приоритет |
|---|---|
| » « | 4 |
| “ш” | 3 |
| “a” | 2 |
| “о” | 2 |
| “с” | 2 |
| (“е”, “п”) | 2 |
| “л” | 1 |
| “M” | 1 |
| Символ | Приоритет |
|---|---|
| » « | 4 |
| “ш” | 3 |
| “a” | 2 |
| “о” | 2 |
| “с” | 2 |
| (“е”, “п”) | 2 |
| (“М”, “л”) | 2 |
| Символ | Приоритет |
|---|---|
| » « | 4 |
| ((“М”, “л”), (“е”, “п”)) | 4 |
| “ш” | 3 |
| “a” | 2 |
| “о” | 2 |
| “с” | 2 |
Действуя далее аналогично:
| Символ | Приоритет |
|---|---|
| » « | 4 |
| ((“М”, “л”), (“е”, “п”)) | 4 |
| (“с”, “о”) | 4 |
| “ш” | 3 |
| “a” | 2 |
| Символ | Приоритет |
|---|---|
| (“a”, “ш”) | 5 |
| » « | 4 |
| ((“М”, “л”), (“е”, “п”)) | 4 |
| (“с”, “о”) | 4 |
| Символ | Приоритет |
|---|---|
| ((“с”, “о”), ((“М”, “л”), (“е”, “п”))) | 8 |
| (“a”, “ш”) | 5 |
| » « | 4 |
| Символ | Приоритет |
|---|---|
| (“ ”, (“a”, “ш”)) | 9 |
| ((“с”, “о”), ((“М”, “л”), (“е”, “п”))) | 8 |
| Символ | Приоритет |
|---|---|
| (((“с”, “о”), ((“М”, “л”), (“е”, “п”))), (“ ”, (“a”, “ш”))) | 17 |
Приоритет последнего оставшегося узла равен длине сообщения.
Изображение соответствующего дерева:
Таким образом, коды символов:
| Символ | Приоритет | Код |
|---|---|---|
| » « | 4 | 10 |
| “ш” | 3 | 111 |
| “a” | 2 | 110 |
| “о” | 2 | 001 |
| “с” | 2 | 000 |
| “л” | 1 | 0101 |
| “M” | 1 | 0100 |
| “п” | 1 | 0111 |
| “е” | 1 | 0110 |
Средний информационный вес символа по формуле Шеннона: \[ H = 4\frac<1><17>\log_2 17 + 3 \frac<2><17>\log_2 \frac<17> <2>+ \frac<3><17>\log_2 \frac<17> <3>+ \frac<4><17>\log_2 \frac<17><4>\] \[ H \approx 2.98 \]
Средний информационный вес по расчету:
Разница оценки по формуле Шеннона и фактической величины не превосходит \[\frac<1> <17>\approx 0.06\]
С ростом общего числа символов в сообщении это различие будет становиться все меньше.
Минимальная сложность сортировки сравнением
Рассмотрим \(\log_2 N!\) :
\[\log_2 N! = \sum_
т.е. для выбора одной перестановки, в отсутствие дополнительной информации о структуре массива, требуется \(\mathcal O(N\log N)\) бит, т.е. \(\mathcal O(N\log N)\) операций сравнения.
Таким образом, для алгоритмов, выполняющих одно сравнение за итерацию, число итераций не может быть лучше \(\mathcal O(N\log N).\)
Содержательный подход. Формулы Хартли и Шеннона.
Американский инженер Р. Хартли в 1928 г. процесс получения информации рассматривал как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определял как двоичный логарифм N.
Формула Хартли: I = log2N или N = 2 i
Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: I = log2100 > 6,644. Таким образом, сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единицы информации.
Приведем другие примеры равновероятных сообщений:
1. при бросании монеты: «выпала решка», «выпал орел»;
2. на странице книги: «количество букв чётное», «количество букв нечётное».
Определим теперь, являются ли равновероятными сообщения«первой выйдет из дверей здания женщина»и«первым выйдет из дверей здания мужчина». Однозначно ответить на этот вопрос нельзя. Все зависит от того, о каком именно здании идет речь. Если это, например, станция метро, то вероятность выйти из дверей первым одинакова для мужчины и женщины, а если это военная казарма, то для мужчины эта вероятность значительно выше, чем для женщины.
Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе.
где pi — вероятность того, что именно i-е сообщение выделено в наборе из N сообщений.
Помимо двух рассмотренных подходов к определению количества информации, существуют и другие. Важно помнить, что любые теоретические результаты применимы лишь к определённому кругу случаев, очерченному первоначальными допущениями.
В качестве единицы информации Клод Шеннон предложил принять один бит (англ. bit — binary digit — двоичная цифра).
Бит в теории информации — количество информации, необходимое для различения двух равновероятных сообщений (типа «орел»—«решка», «чет»—«нечет» и т.п.).
В вычислительной технике битом называют наименьшую «порцию» памяти компьютера, необходимую для хранения одного из двух знаков «0» и «1», используемых для внутримашинного представления данных и команд.
Бит — слишком мелкая единица измерения. На практике чаще применяется более крупная единица — байт, равная восьми битам. Именно восемь битов требуется для того, чтобы закодировать любой из 256 символов алфавита клавиатуры компьютера (256=2 8 ).
Широко используются также ещё более крупные производные единицы информации:
1 Килобайт (Кбайт) = 1024 байт = 210 байт,
1 Мегабайт (Мбайт) = 1024 Кбайт = 220 байт,
1 Гигабайт (Гбайт) = 1024 Мбайт = 230 байт.
В последнее время в связи с увеличением объёмов обрабатываемой информации входят в употребление такие производные единицы, как:
1 Терабайт (Тбайт) = 1024 Гбайт = 240 байт,
1 Петабайт (Пбайт) = 1024 Тбайт = 250 байт.
За единицу информации можно было бы выбрать количество информации, необходимое для различения, например, десяти равновероятных сообщений. Это будет не двоичная (бит), а десятичная (дит) единица информации.
Количество информации, заключенное в сообщении, определяется объемом знаний, который несет это сообщение получающему его человеку. Сообщение содержит информацию для человека, если заключенные в нем сведения являются для этого человека новыми и понятными, и, следовательно, пополняют его знания.
При содержательном подходе возможна качественная оценка информации: полезная, безразличная, важная, вредная, … Одну и туже информацию разные люди могут оценить по-разному.
Информацию, которую получает человек, можно считать мерой уменьшения неопределенности знаний. Если некоторое сообщение приводит к уменьшению неопределенности наших знаний, то можно говорить, что такое сообщение содержит информацию.
За единицу количества информации принято такое количество информации, которое мы получаем при уменьшении неопределенности в 2 раза. Такая единица названа бит.
В компьютере информация представлена в двоичном коде или на машинном языке, алфавит которого состоит из двух цифр (0 и 1). Эти цифры можно рассматривать как два равновероятных состояния. При записи одного двоичного разряда реализуется выбор одного из двух возможных состояний (одной из двух цифр) и, следовательно, один двоичный разряд несет количество информации в 1 бит. Два двоичных разряда несут информацию 2 бита, три разряда – 3 бита и т.д.
Поставим теперь обратную задачу и определим: «Какое количество различных двоичных чисел N можно записать с помощью I двоичных разрядов?» С помощью одного двоичного разряда можно записать 2 различных числа (N=2=2 1 ), с помощью двух двоичных разрядов можно записать четыре двоичных числа (N=4=2 2 ), с помощью трех двоичных разрядов можно записать восемь двоичных чисел (N=8=2 3 ) и т.д.
В общем случае количество различных двоичных чисел можно определить по формуле
где I – количество информации;
N – количество возможных событий (равновероятных). ;
В математике существует функция, с помощью которой решается показательное уравнение, эта функция называется логарифмом. Решение такого уравнения имеет вид:
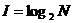
Если события равновероятны, то количество информации определяется по данной формуле.
Количество информации для событий с различными вероятностями определяется по формуле Шеннона:
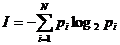
где I – количество информации;
N – количество возможных событий;
Pi – вероятность отдельных событий.
Пример 3.4
В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержит сообщение о первом выпавшем номере (например, выпал номер 15)?
Поскольку вытаскивание любого из 32 шаров равновероятно, то количество информации об одном выпавшем номере находится из уравнения: 2 I =32.
Пример 3.5
Какое количество вопросов достаточно задать вашему собеседнику, чтобы наверняка определить месяц, в котором он родился?
Будем рассматривать 12 месяцев как 12 возможных событий. Если спрашивать о конкретном месяце рождения, то, возможно, придется задать 11 вопросов (если на 11 первых вопросов был получен отрицательный ответ, то 12-й задавать не обязательно, так как он и будет правильным).
Правильнее задавать «двоичные» вопросы, то есть вопросы, на которые можно ответить только «да» или «нет». Например, «Вы родились во второй половине года?». Каждый такой вопрос разбивает множество вариантов на два подмножества: одно соответствует ответу «да», а другое – ответу «нет».
Правильная стратегия состоит в том, что вопросы нужно задавать так, чтобы количество возможных вариантов каждый раз уменьшалось вдвое. Тогда количество возможных событий в каждом из полученных подмножеств будет одинаково и их отгадывание равновероятно. В этом случае на каждом шаге ответ («да» или «нет») будет нести максимальное количество информации (1 бит).
По формуле 2 и с помощью калькулятора получаем:

Количество полученных бит информации соответствует количеству заданных вопросов, однако количество вопросов не может быть нецелым числом. Округляем до большего целого числа и получаем ответ: при правильной стратегии необходимо задать не более 4 вопросов.
Пример 3.6
После экзамена по информатике, который сдавали ваши друзья, объявляются оценки («2», «3», «4» или «5»). Какое количество информации будет нести сообщение об оценке учащегося А, который выучил лишь половину билетов, и сообщение об оценке учащегося В, который выучил все билеты.
Опыт показывает, что для учащегося А все четыре оценки (события) равновероятны и тогда количество информации, которое несет сообщение об оценке, можно вычислить по формуле (1):
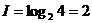
На основании опыта можно также предположить, что для учащегося В наиболее вероятной оценкой является «5» (p1=1/2), вероятность оценки «4» в два раза меньше (p2=1/4), а вероятности оценок «2» и «3» еще в два раза меньше (p3 =p4=1/8). Так как события неравновероятны, воспользуемся для подсчета количества информации в сообщении формулой 2:
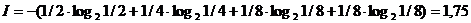
Вычисления показали, что при равновероятных событиях мы получаем большее количество информации, чем при неравновероятных событиях.
Пример 3.7
В непрозрачном мешочке хранятся 10 белых, 20 красных, 30 синих и 40 зеленых шариков. Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика.
Так как количество шариков разного цвета неодинаково, то вероятности зрительных сообщений о цвете вынутого из мешочка шарика также различаются и равны количеству шариков данного цвета деленному на общее количество шариков:
События неравновероятны, поэтому для определения количества информации, содержащегося в сообщении о цвете шарика, воспользуемся формулой 2:

Для вычисления этого выражения, содержащего логарифмы можно воспользоваться калькулятором. I»1,85 бита.
Пример 3.8
Используя формулу Шеннона, достаточно просто определить, какое количество бит информации или двоичных разрядов необходимо, чтобы закодировать 256 различных символов. 256 различных символов можно рассматривать как 256 различных равновероятных состояний (событий). В соответствии с вероятностным подходом к измерению количества информации необходимое количество информации для двоичного кодирования 256 символов равно:
I=log2256=8 бит=1 байт
Следовательно, для двоичного кодирования 1 символа необходим 1 байт информации или 8 двоичных разрядов.
Какое количество информации содержится, к примеру, в тексте романа «Война и мир», во фресках Рафаэля или в генетическом коде человека? Ответа на эти вопросы наука не даёт и, по всей вероятности, даст не скоро. А возможно ли объективно измерить количество информации? Важнейшим результатом теории информации является следующий вывод:«В определенных, весьма широких условиях можно пренебречь качественными особенностями информации, выразить её количество числом, а также сравнить количество информации, содержащейся в различных группах данных».
В настоящее время получили распространение подходы к определению понятия «количество информации», основанные на том, что информацию, содержащуюся в сообщении, можно нестрого трактовать в смысле её новизны или, иначе, уменьшения неопределённости наших знаний об объекте. Эти подходы используют математические понятия вероятности и логарифма.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.