Докажите что функция общего вида
Четные и нечетные функции
Вы будете перенаправлены на Автор24
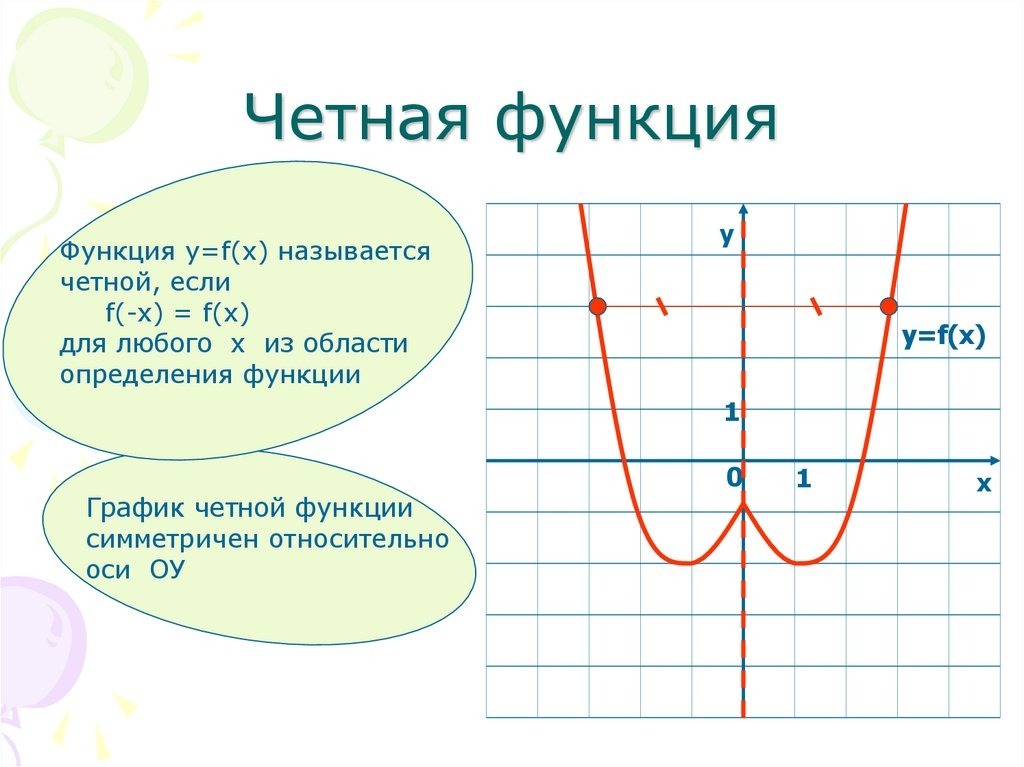
Четные функции
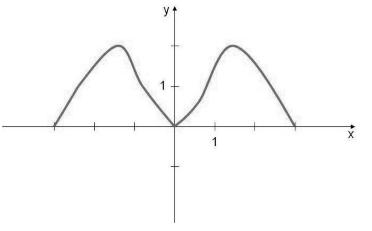
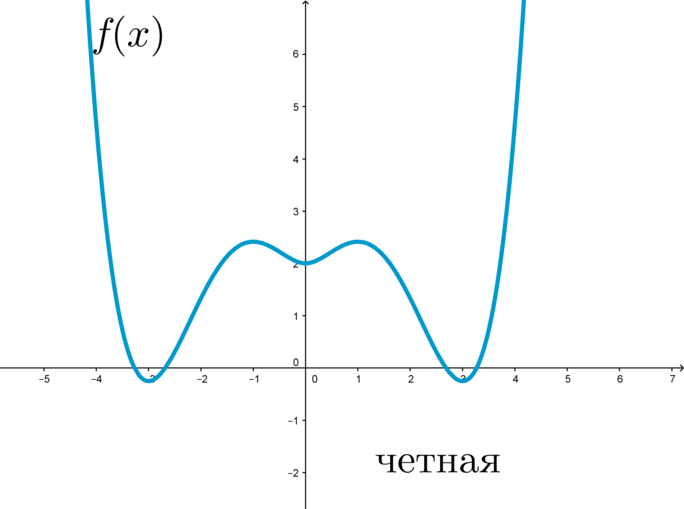
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будет совпадать, то график этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).
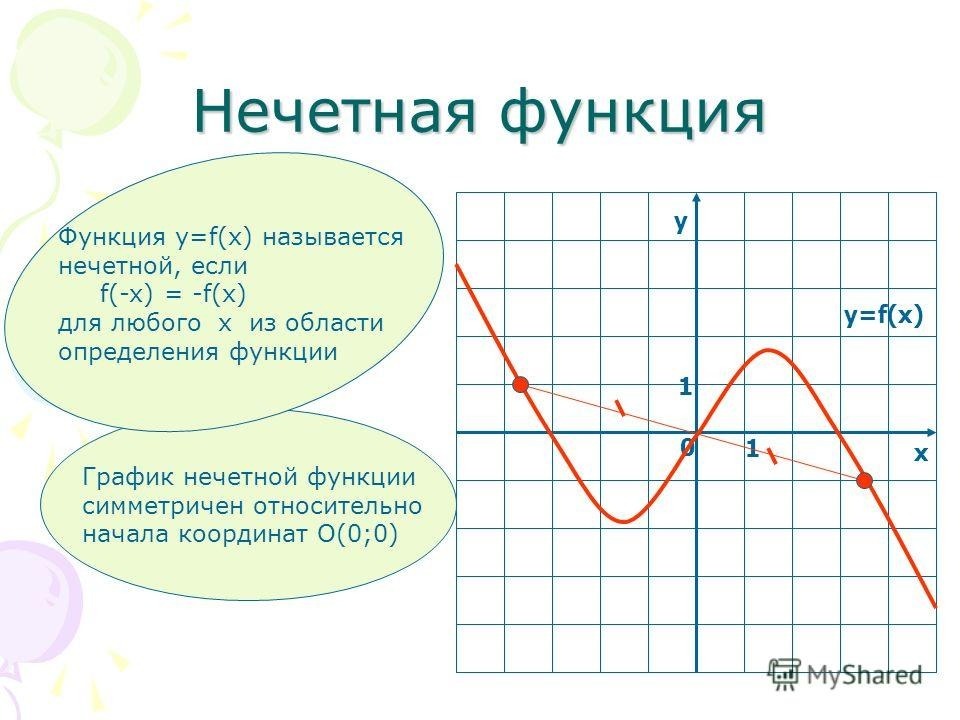
Нечетные функции
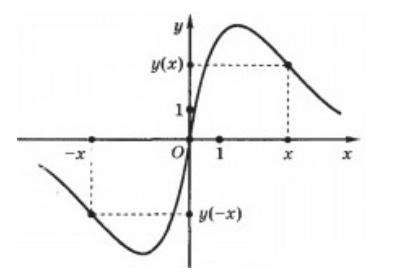
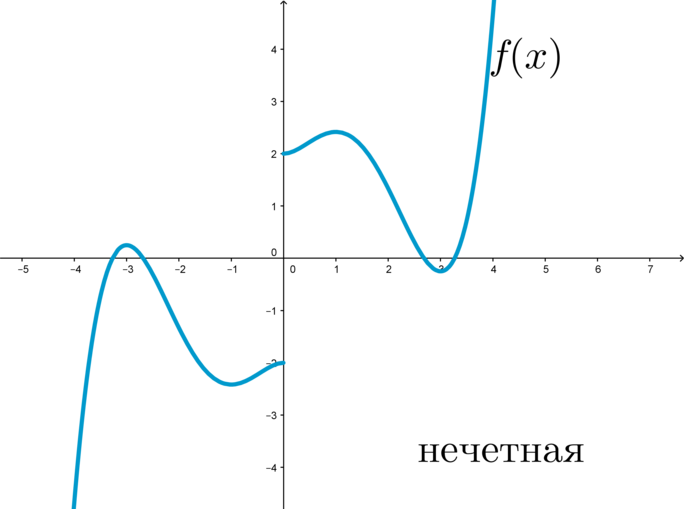
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будут также совпадать по модулю и отрицательны по знакам, то график этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).
Готовые работы на аналогичную тему
Функция общего вида
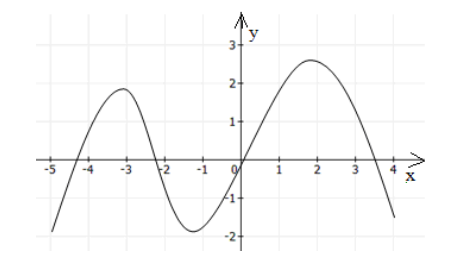
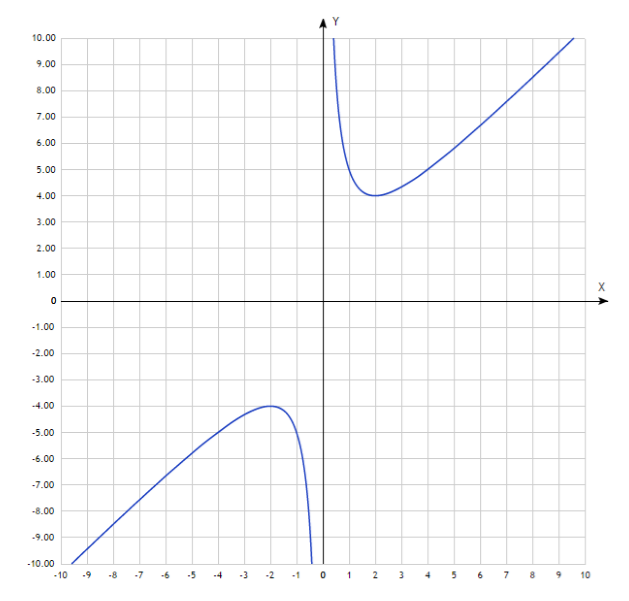
Функция общего вида никогда не будет симметрична оси ординат и началу координат. Пример функции общего вида изображен на рисунке 3.
Пример задачи
Исследовать функцию на четность и нечетность и построить их графики.
Изобразим её на графике:
Изобразим её на графике:
Изобразим её на графике:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 04 07 2021
Четные и нечетные функции
График четной функции симметричен относительно оси \(y\) :
График нечетной функции симметричен относительно начала координат:
\(\blacktriangleright\) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.
\(\blacktriangleright\) Некоторые свойства:
1) Произведение и частное двух функций одинаковой четности — четная функция.
2) Произведение и частное двух функций разной четности — нечетная функция.
3) Сумма и разность четных функций — четная функция.
4) Сумма и разность нечетных функций — нечетная функция.
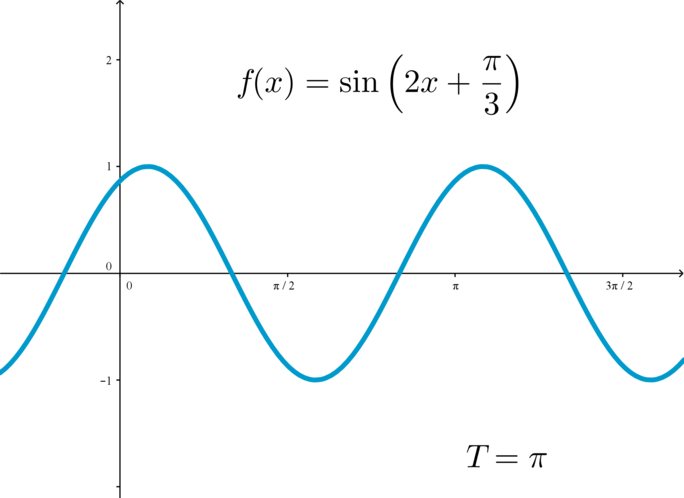
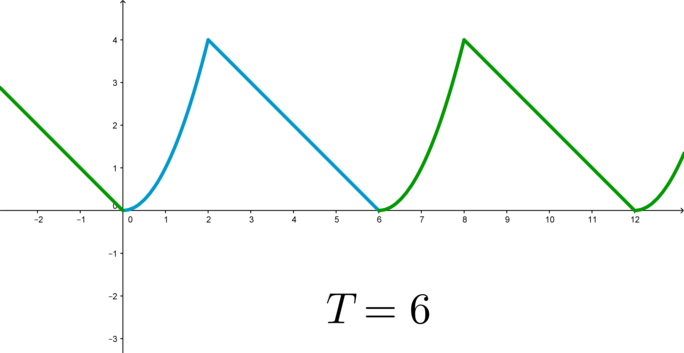
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной \(T\) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:
При каких значениях параметра \(a\) уравнение
имеет единственное решение?
\[2\cdot 0+a\mathrm
симметричен относительно начала координат.
Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)
\(\dfrac n2, n\in\mathbb
(Задача от подписчиков)
имеет хотя бы один корень.
(Задача от подписчиков)
имеет шесть различных решений.
Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.
1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \[D=a^2-16a+52>0\quad\Leftrightarrow\quad a\in (-\infty;8-2\sqrt3)\cup(8+2\sqrt3;+\infty)\]
2) Также нужно, чтобы оба корня были положительными (так как \(t>0\) ). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно: \[\begin
Понятие четной и нечетной функции
Понятие четности и нечетности функции
Главное условие при исследовании функции на четность/нечетность — это симметричность области определения относительно 0. Если она не симметрична, то функция не является ни четной, ни нечетной, и дальнейшее исследование производить не нужно. Например, \(D(y)\in(-\infty;+\infty)\) симметрична относительно 0, а \(D(y):x\in(-5;9)\) — нет.
Четная функция
Функцию \(f(x)\) называют четной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=f(x).\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
График четной функции симметричен относительно оси Ох.
Нечетная функция
Функцию \(f(x)\) называют нечетной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=-f(x).\)
График нечетной функции симметричен относительно начала координат (точки (0;0)).
Произведение четной и нечетной функции
Произведение четной и нечетной функций есть нечетная функция.
Пусть \(f(x)\) — четная функция, а \(g(x)\) — нечетная. Тогда \(f(x)=f(-x), а g(-x)=-g(x).\)
Исследование функций в примерах
Доказать, что функция \(y=x^2\) четная.
1. Найдем область определения: \(D(y):x\in(-\infty;+\infty)\) — симметрична относительно 0.
Исследовать на четность и нечетность функцию \(f(x)=8x^3-7x.\)
1. Найдем область определения: \(D(f):x\in(-\infty;+\infty)\) — симметрична относительно 0.
Исследовать на четность и нечетность функции \(f_1(x)=\frac
Рассмотрим первую функцию:
1. Найдем область определения: x — любое число, кроме 1. Она не симметрична относительно 0, значит \( f_1(x)\) относится к функциям общего вида, то есть не является ни четной ни нечетной.
Рассмотрим вторую функцию:
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
теория по математике 📈 функции
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Таким образом, мы нашли нуль функции: х=2
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
График линейной функции, его свойства и формулы
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!
Свойства линейной функции
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Точки пересечения графика функции y = kx + b с осями координат:
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).