Докажите что каждая сторона треугольника меньше суммы двух других сторон

Существующие треугольники

Определение

Существующие треугольники — это такие треугольники,
существование которых можно доказать с помощью неравенств.

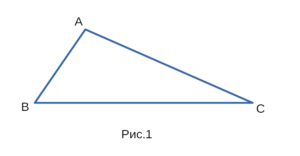
Например существование треугольника, изображенного на рисунке 1,
можно доказать с помощью неравенств: AB + BC > AC, AC + BC > AB, AB + AC > BC
Если эти три неравенства истинны значит треугольник существует,
иначе он не существует.

Также существование того или иного треугольника можно проверить с
помощью одного условия: Если большая сторона треугольника меньше
суммы двух других сторон, значит треугольник существует,
иначе он не существует.

Теорема

Для доказательства того, о чем мы говорили существует теорема под названием неравенство треугольника. Формулировка теоремы:
каждая сторона треугольника меньше суммы двух других сторон.

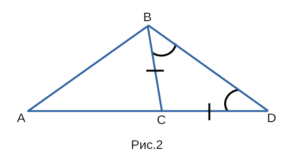
Докажем, что каждая сторона треугольника, изображенного на рисунке 2, меньше суммы двух других сторон:

Доказательство теоремы

Источник

Неравенство треугольника

Урок 22. Геометрия 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Неравенство треугольника»

Вспомним теорему о соотношениях между сторонами и углами треугольника:

В треугольнике против большей стороны лежит больший угол, и наоборот, против большего угла лежит большая сторона.

Воспользуемся этой теоремой при доказательстве неравенства треугольника.

Длина любой стороны треугольника меньше суммы двух других его сторон.

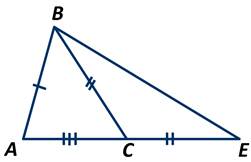
Отложим на луче АС отрезок СЕ=ВС.

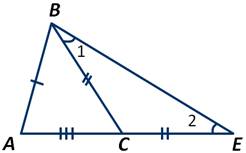
В треугольнике АВЕ угол ∠АВЕ>∠1, следовательно, ∠АВЕ>∠2.

А так как в треугольнике против большего угла лежит большая сторона, то АВ Оцените видеоурок

Источник