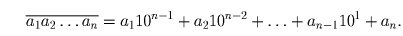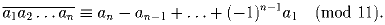Докажите что количество четырехзначных чисел равно количеству шестизначных чисел в записи которых

18.04.202223.04.2022 admin 0 Comments

Докажите, что количество четырёхзначных чисел равно количеству шестизначных чисел, в записи которых вторая и пятая цифры (считая слева направо) соответственно равны 0 и 4

Ответы 10

В рассматриваемом шестиразрядном числе abcdef, разряд “a” может принимать значения от 1 до 9 (9 значений), разряд “b” может принимать значения от 0 до 0 (1 значение), разряд “c” может принимать значения от 0 до 9 (10 значений), разряд “d” может принимать значения от 0 до 9 (10 значений), разряд “e” может принимать значения от 4 до 4 (1 значение), разряд “а” может принимать значения от 0 до 9 (10 значений).

Посчитаем всевозможное количество значений, которое может принимать число abcdef.

Точно также посчитаем всевозможное количество значений, которое может принимать четырехзначное число wxyz, у которого разряд “w” может принимать значения 1 до 9 (9 значений), разряд “x” может принимать значения от 0 до 9 (10 значений), разряд “y” может принимать значения от 0 до 9 (10 значений), разряд “я” может принимать значения от 0 до 9 (10 значений).

Как видим M=N. Число шестизначных чисел с двумя неизменяемыми разрядами равно числу четырехзначных чисел.

Источник

Докажите что количество четырехзначных чисел равно количеству шестизначных чисел в записи которых

Задача 24:

Докажите, что любое натуральное число сравнимо со своей последней цифрой по модулю а) 10; б) 2; в) 5.

Решение:

Вычтем из числа его последнюю цифру и получим число, оканчивающееся нулем, т.е. делящееся на 10 (а значит, и на 5, и на 2).

Задача 25:

Докажите, что .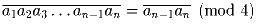

Решение:

Указание: все степени десяти, начиная со 100, делятся на 4.

Задача 26:

Решение:

Число делится на 2 n (на 5 n ) тогда и только тогда, когда число, образованное его последними n цифрами, делится на 2 n (на 5 n ).

Задача 27:

Последняя цифра квадрата натурального числа равна 6. Докажите, что его предпоследняя цифра нечетна.

Решение:

Так как последняя цифра 6, то возводимое в квадрат число четно. Раз оно является квадратом, то оно делится и на 4. Следовательно, число, составленное из двух его последних цифр, должно делиться на 4. Все требуемые двузначные числа легко выписать: 16, 36, 56, 76, 96.

Задача 28:

Предпоследняя цифра квадрата натурального числа – нечетная. Докажите, что его последняя цифра 6.

Решение:

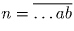
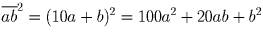
Две последние цифры квадрата числа n зависят только от двух последних цифр числа n. Пусть . Тогда . Ясно, что цифра десятков числа b² должна быть нечетной. Прямой перебор показывает, что цифра единиц должна тогда быть равной 6.

Задача 29:

Докажите, что степень двойки не может оканчиваться четырьмя одинаковыми цифрами.

Решение:

Рассмотрите остатки по модулю 16.

Задача 30:

Найдите 100-значное число без нулевых цифр, которое делится на сумму своих цифр.

Решение:

Подберем число так, чтобы сумма его цифр равнялась 125. Делимость числа на 125 определяется тремя его последними цифрами. Следовательно, годится число 111 … 11599125 (в начале записи единица написана 94 раза).

Задача 31:

Докажите, что любое натуральное число сравнимо с суммой своих цифр по модулю а) 3; б) 9.

Решение:

Ясно, что 10 ≡ 1 (mod %)%9. Поэтому 10 k ≡ 1 (mod 9) для любого натурального k. Таким образом, a ₁ 10 n – 1 + a ₂ 10 n – 2 + … + a _{n – 1} 10¹ + a _n ≡ a ₁ + a ₂ + … + a _n (mod %)%9. Рассуждения для числа 3 совершенно аналогичны.

Задача 32:

Решение:

а) нет; б) нет. Рассмотрите остатки по модулю 9.

Задача 33:

У числа 2¹ºº нашли сумму цифр, у результата снова нашли сумму цифр и т.д. В конце концов получилось однозначное число. Найдите его.

Решение:

Задача 34:

Докажите, что если записать в обратном порядке цифры любого натурального числа, то разность исходного и нового числа будет делиться на 9.

Решение:

Эти числа имеют одинаковые суммы цифр и, значит, одинаковые остатки по модулю 9.

Задача 35:

К числу 15 припишите слева и справа по одной цифре так, чтобы полученное число делилось на 15.

Решение:

Это можно сделать шестью способами: 1155, 4155, 7155, 3150, 6150, 9150.

Задача 36:

Сколько имеется четырехзначных чисел, которые делятся на 45, а две средние цифры у них – 97?

Решение:

Два числа: 6975, 2970.

Задача 37:

Найдите наименьшее натуральное число, делящееся на 36, в записи которого встречаются все 10 цифр.

Решение:

Это число 1023457896.

Задача 38:

Докажите, что произведение последней цифры числа 2 n и суммы всех цифр этого числа, кроме последней, делится на 3.

Решение:

Разберите два случая: последняя цифра равна или не равна 6.

Задача 39:

Может ли сумма цифр точного квадрата равняться 1970?

Решение:

Нет. Рассмотрите остатки по модулю 3.

Задача 40:

Из трехзначного числа вычли сумму его цифр. С полученным числом проделали то же самое и так далее, 100 раз. Докажите, что в результате получится нуль.

Решение:

Задача 41:

Решение:

Задача 42:

Решение:

Указание: 10 ≡ – 1 (mod 11).

Задача 43:

Докажите, что число 111 … 11 (2n единиц) – составное.

Решение:

Это число делится на 11.

Задача 44:

Докажите, что число 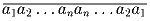– составное.

Решение:

Это число делится на 11.

Задача 45:

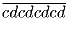
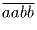
Пусть a, b, c, d – различные цифры. Докажите, что не делится на .

Решение:

делится на 11, а – нет.

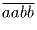
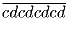
Задача 46:

A – шестизначное число, в записи которого по одному разу встречаются цифры 1, 2, 3, 4, 5, 6. Докажите, что A не делится на 11.

Решение:

Цифры 1, 2, 3, 4, 5, 6 нельзя разбить на две тройки, разность сумм в которых делится на 11.

Задача 47:

Докажите, что разность числа, имеющего нечетное количество цифр, и числа, записанного теми же цифрами, но в обратном порядке, делится на 99.

Решение:

Эти два числа имеют одинаковые остатки как при делении на 9, так и при делении на 11.

Задача 48:

Можно ли составить из цифр 2, 3, 4, 9 (каждую цифру можно использовать сколько угодно раз) два числа, одно из которых в 19 раз больше другого?

Решение:

Нельзя. Проследите за последней цифрой.

Задача 49:

Сумма двух цифр a и b делится на 7. Докажите, что число 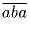также делится на 7.

Решение:

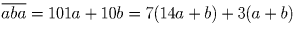
Задача 50:

Сумма цифр трехзначного числа равна 7. Докажите, что это число делится на 7 тогда и только тогда, когда две его последние цифры равны.

Решение:

, так как 2(a + b + c) ≡ 0 (mod 7). Значит, делится на 7 тогда и только тогда, когда b – c делится на 7. Но так как b, c

Источник

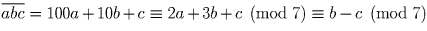
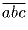
Задачи по комбинаторике. Часть 1

В этой статье использован материал из лекций Шарича Владимира Златковича и Максимова Дмитрия Васильевича на КПК foxford.

Очень рекомендую абитуриентам курсы foxford для подготовки к ЕГЭ и олимпиадам.

1. Сколько четырехзначных чисел содержит ровно одну семерку?

Четырехзначное число имеет вид . Если четырехзначное число содержит ровно одну семерку, то она может стоять

1) на первом месте, и тогда на остальных трех местах могут стоять любые цифры от 0 до 9, кроме цифры 7, и по правилу произведения мы получаем четырехзначных чисел, у которых семерка стоит на первом месте.

Сложим полученные варианты, и получим четырехзначных чисел, содержащих ровно одну семерку.

2. Сколько пятизначных чисел содержит ровно две семерки?

Так же как в предыдущей задаче у нас две возможности:

1) Одна из семерок стоит на первом месте, а вторая на любом из оставшихся четырех мест. На трех местах, не занятых цифрой 7 может стоять любая из 9 цифр (все, кроме цифры 7). В этом случае мы получаем чисел.

2) Ни одна из семерок не стоит на первом месте. В этом случае мы имеем возможностей расставить 2 семерки на оставшихся 4-х местах. У нас осталось 3 места, не занятых цифрой 7, одно из которых первое, и таким образом мы получаем чисел.

Сложим полученные варианты, и получим пятизначных чисел, содержащих ровно две семерки.

3. Сколько существует пятизначных чисел, цифры которых различны и расположены в порядке возрастания?

Так как первой цифрой не может быть 0, рассмотрим последовательность цифр 1-9, расположенных в порядке возрастания.

Если мы выберем из этой последовательности 5 произвольных цифр, например так:

то получим пятизначное число, цифры которого различны и расположены в порядке возрастания.

Осталось посчитать, сколькими способами мы можем выбрать из 9 цифр 5:

Итак существует 126 пятизначных чисел, цифры которых различны и расположены в порядке возрастания.

Треугольник Паскаля и число сочетаний.

4. Задача о хромом короле. Пусть есть доска размером . Король находится в левом верхнем углу доски и может перемещаться по доске, двигаясь только вправо и вниз. Сколькими способами король может добраться до левого нижнего угла доски?

Посчитаем, для каждой клетки, сколькими способами король может до нее добраться.

Так как король может двигаться только вправо и вниз, до любой клетки первого столбца и первой строки он может добраться единственным способом:

Рассмотрим произвольную клетку доски. Если в клетку, стоящую над ней можно добраться способами, а в клетку, стоящую слева от нее способами, то в саму клетку можно добраться способами (это следует из того, что король может двигаться только вправо и вниз, то есть не может дважды зайти на одну клетку):

Заполним начальные клетки, пользуясь этим правилом:

Мы видим, что при заполнении клеток у нас получается треугольник Паскаля, только повернутый на бок.

Число в каждой клетке показывает, сколькими способами король может попасть в эту клетку из левой верхней.

То есть найти, скольким способами мы можем расположить 2 вертикальные (или 3 горизонтальные) стрелки на 5-ти местах. Число способов равно:

— то есть ровно то число, которое стоит в этой клетке.

Для того, чтобы попасть в последнюю клетку, король должен сделать всего шага, из которых по вертикали. Таким образом, он может попасть в последнюю клетку

Можно получить рекуррентное соотношение для числа сочетаний:

Смысл этого соотношения следующий. Путь у нас есть множество, состоящее из n элементов. И нам нужно выбрать из этого множества l элементов. Все способы, которыми мы можем это сделать делятся на две группы, которые не пересекаются. Мы можем:

а) зафиксировать один элемент, и из оставшихся n-1-го элемента выбрать l-1 элемент. Это можно сделать способами.

б) выбрать из оставшихся n-1-го элемента все l элементов. Это можно сделать способами.

Также можно получить соотношение:

Кроме того, число подмножеств с четным числом элементов равно числу подмножеств с нечетным числом элементов:

Докажем это соотношение. Для этого докажем, что между подмножествами с четным числом элементов и подмножествами с нечетным числом элементов существует взаимно однозначное соответствие.

Зафиксируем один элемент множества:

5. Рассмотрим выражение

1. Сколько слагаемых имеет этот многочлен?

а) до приведения подобных членов

б) после приведения подобных членов.

2. Найти коэффициент при произведении

При возведении суммы слагаемых в степень , мы должны эту сумму умножить на себя раз. Мы получаем сумму одночленов, степень каждого из которых равна m. Число всевозможных произведений, состоящих из переменных из множества с учетом порядка и возможностью повторения равно числу размещений с повторениями из k по m:

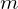
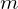
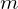
Когда мы приводим подобные члены, мы считаем одинаковыми произведения, содержащие равное число множителей каждого вида. В этом случае, чтобы найти число слагаемых многочлена после приведения подобных членов, мы должны найти число сочетаний с повторениями из k по m:

Найдем коэффициент при произведении .

Выражение представляет собой произведение m элементов из множества , причем элемент взят раз, элемент взят раз, и так далее, и, наконец, элемент взят раз. Коэффициент при произведении равен числу возможных произведений:

Рассмотрим частный случай: — Бином Ньютона. И получим формулу для биномиальных коэффициентов.

Тогда если мы положим х=1 и y=1, то получим, что

6. Задача про кузнечика.

Есть n клеточек, расположенных последовательно. Кузнечик должен попасть из крайней левой клеточки в крайнюю правую, прыгая вправо на произвольное число клеток.

а) Сколькими способами он может это сделать?

Изобразим условие задачи:

Кузнечик может попасть в крайнюю правую клетку, побывав, или не побывав в любой внутренней клетке. Присвоим клетке значение 1, если кузнечик в ней побывал, и 0, если нет, например, так:

Тогда у нас есть n-2 клеточек, каждая из которых может принимать значение 0 или 1. Задача сводится к нахождению числа последовательностей, состоящих из n-2 нулей и единиц. Таких последовательностей .

б) сколькими способами кузнечик может добраться в n-ю клетку, сделав k шагов?

Чтобы попасть в n-ю клетку, сделав k шагов, кузнечик должен попасть ровно в k—1 клетку между первой и последней. Так как последний шаг он делает всегда в последнюю клетку. То есть стоит вопрос, сколькими способами можно выбрать k—1 клетку из n-2 клеток?

Ответ: .