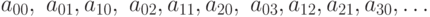Докажите что квадрат равномощен отрезку
Счетные множества
Множество называется счетным, если оно равномощно множеству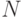 
натуральных чисел, то есть если его можно представить в виде 
(здесь 
— элемент, соответствующий числу 
; соответствие взаимно однозначно, так что все различны).
Например, множество целых чисел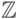 
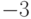
счетно, так как целые числа можно расположить в последовательность 
, 
, 
, 
, 
, 
, 
, 
(а) Подмножество счетного множества конечно или счетно.
(в) Объединение конечного или счетного числа конечных или счетных множеств конечно или счетно.
(а) Пусть 
— подмножество счетного множества 
. Выбросим из последовательности 
те члены, которые не принадлежат (сохраняя порядок оставшихся). Тогда оставшиеся члены образуют либо конечную последовательность (и тогда конечно), либо бесконечную (и тогда счетно).
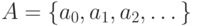
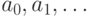
(в) Пусть имеется счетное число счетных множеств 
Расположив элементы каждого из них слева направо в последовательность ( 
) и поместив эти последовательности друг под другом, получим таблицу
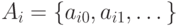
Замечание. В доказательстве утверждения (б) теоремы 2 есть тонкий момент: на каждом шаге мы должны выбрать один из оставшихся элементов множества 
; такие элементы есть, но у нас нет никакого правила, позволяющего такой выбор описать. При более формальном построении теории множеств тут нужно сослаться на специальную аксиому, называемую аксиомой выбора. Законность этой аксиомы вызывала большие споры в начале 20-го века, но постепенно к ней привыкли, и эти споры сейчас почти не воспринимаются. В середине века великий логик Курт Гедель доказал, что аксиому выбора нельзя опровергнуть, пользуясь остальными аксиомами теории множеств, а в 1960-е годы американский математик Пол Дж.Коэн доказал, что ее нельзя и вывести из остальных аксиом. (Конечно, понимание этих утверждений требует подробного изложения теории множеств как аксиоматической теории.)
30. Такой же тонкий момент (хотя и менее очевидный) есть и в доказательстве утверждения (в). Можете ли вы догадаться, где он? (Ответ: мы знаем, что множества 
счетны, то есть что существует взаимно однозначное соответствие между 
и . Но нужно выбрать и фиксировать эти соответствия, прежде чем удастся построить соответствие между объединением всех и .)
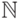
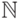
Еще несколько примеров счетных множеств:
31. Докажите, что любое семейство непересекающихся интервалов на прямой конечно или счетно. (Указание: в каждом интервале найдется рациональная точка.)
33. Докажите, что множество точек строгого локального максимума любой функции действительного аргумента конечно или счетно.
Докажите, что множество точек разрыва неубывающей функции Действительного аргумента конечно или счетно.
Математический портал
Nav view search
Navigation
Search
Счетность и несчетность множеств. Равномощность множеств.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Примеры.
Доказать, что следующие множества счетны:
Решение.
Что и требовалось доказать.
Решение.
Что и требовалось доказать.
Решение.
Что и требовалось доказать.
Решение.
Что и требовалось доказать.
Примеры:
Доказательство.
Что и требовалось доказать.
Доказательство.
Проведем доказательство в несколько этапов:
Что и требовалось доказать.
Домашнее задание.
Доказать, что следующие множества счетны:
1.70. Используя результат задачи 1.68, доказать, что множество всех точек плскости с рациональными координатами счетно.
08. Примеры равномощных множеств
Приведенные выше примеры и теоремы показывают, что установить равномощность различных множеств далеко не просто. В этом параграфе мы рассмотрим примеры построения биекции между различными множествами. Будут приведены примеры доказательств равномощности ряда множеств.
Пример 1. Установить биекцию между отрезком [0, 1] и отрезком [а, в].
Решение. Легко устанавливается биективность линейного отображения x = (в – a)t + a отрезка [0, 1] на отрезок [а, в].
Пример 2. Установить биекцию между интервалом (0, 1) и интервалом (–¥, +¥).
Решение. Легко устанавливается биективность отображения x= ctg(pt) интервала (0, 1) на интервал (–¥, +¥).
Задача. Рассмотреть основные элементарные функции и найти промежутки, на которых они являются биективным отображением.
Пример 3. Построить биекцию между отрезком [0, 1] и интервалом (0, 1).
Решение. Решение этой задачи основано на несчетности рассматриваемых множеств и теореме 4 из параграфа 6. Идея решения состоит в том, что из интервала (0, 1) выделяют некоторое счетное множество А. Затем к нему добавляют две точки <0>и <1>. Вновь полученное множество (обозначим его В Ì [0, 1]), также является счетным. Следовательно, множества А и В равномощны и существует биекция f, отображающая B на A. Построим теперь биекцию отрезка [0, 1] на интервал (0, 1) следующим образом:
Пример 4. Построить биекцию между окружностью единичного радиуса и отрезком [0, 1].
Схема решения. Легко устанавливается биекция между точкой окружности и углом, соответствующим этой точке. Этим получается биекция окружности и полуотрезка [0, 2p). Затем по схеме примера 3 строится биекция полуотрезка [0, 2p) на отрезок [0, 1].
Пример 6. Доказать, что множество точек разрыва монотонной функции, заданной на отрезке [а, в], конечно или счетно.
Как постоить биекцию между квадратом и отрезком?
Здравствуйте, уважаемые преподаватели!
Знаю, что мощность отрезка [0; 1] равно мощности континуума. И знаю, что декартово произведение двух отрезков, то есть единичный квадрат, имеет такую же мощность.
Значит, между этими множествами существует биекция. А как её построить?
Вот что я нашла в книге Р.Курант, Г.Роббинс. Что такое математика? на c.112-113
Но я не понимаю, как можно видоизменить указанное построение=(
Павел Борисович, спасибо Вам большое! Я все поняла!
А приведенное выше доказательство из книги (которое я привела) придумал Кантор, как я поняла. Я очень много вчера литературы по этому поводу прочитала.
Да, а я думала над другим способом обойти проблему с «плохими точками». Хотела просто то же самое преобразование — склеивание двух координат точки квадрата, производить в двоичной системе счисления. Там же нет 9-ок=). Но потом поняла, что проблема и в этом случае никуда не исчезает: ведь ( 0.(1) )_2 = ( 1 )_2 = ( 1.(0) )_2
Это просто чтобы Вы не думали, что я только задаю вопросы — а сама ничего не делаю.
Да, согласна. Но мы можем отбросить все последовательности с 1 в периоде в принципе, кроме одной ( 0.(1) )_2, которая как раз и получается при склеивании координат правой верхней вершины квадрата, то есть двух таких же последовательностей.
Тогда у нас все точки отрезка будут образами каких-то точек квадрата.
Да? То есть нет смысла переходить в двоичную систему счисления?
Докажите что квадрат равномощен отрезку
Напомню вопрос.
Он заключался в том, имеют ли квадрат и его сторона равные мощности. То есть, равно ли в них «количество точек»? Сравнимы ли типы бесконечности для обозначения количества точек отрезка и количества точек двумерной фигуры?
На первый взгляд, ответ очевиден: «конечно же нет!» Ведь в квадрате помещается бесконечное число отрезков длиной в его сторону!
Однако, чтобы доказать, что это не так, что множества эти «соизмеримы», и более того, равномощны, («имеют одинаковое количество точек"
, нам надо всего лишь задать взаимно однозначное соответствие из точек квадрата в точки его стороны (и обратно).
Оговорюсь сразу: я не могу найти, где я это вычитала, и поэтому не помню в точности, как там выглядит «предельный переход» — отображение точек, которые лежат на сторонах квадрата. С внутренней областью всё ясно. А насчет границы: это уже мой личный изворот.
То есть, х и у будут представлять собой конечные или бесконечные десятичные дроби в диапазоне от 0 до 1.
Теперь обратимся к точкам на границе.
В одном из комментариев в этом сообществе я уже показывала, что когда речь идет от числах вещественных, две записи единицы полностью эквивалентны:
1,0000000000000000. = 0,999999999999999999999.
Поэтому точки на границах квадрата мы будем представлять с соответствующей координатой (у для верхней стороны и х — для правой) равной 0,9999999.
Тогда отображение ЛЮБОЙ точки квадрата на отрезок оси от 0 до 1 можно представить в следующем виде:
Сумбурно несколько вышло.
Поэтому, если что, — говорите сразу.