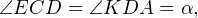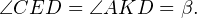Докажите что медиана проведенная к основанию равнобедренного треугольника перпендикулярна основанию

1докажите что медиана проведенная к основанию равнобедренного треугольника перпендикулярна основанию 2докажите что медиана проведенные к боковым сторонам равнобедренного треугольника равны?

1докажите что медиана проведенная к основанию равнобедренного треугольника перпендикулярна основанию 2докажите что медиана проведенные к боковым сторонам равнобедренного треугольника равны.

3Докажите, что длина отрезка, соед.

Середины двух сторон рреугольника равна половине длины третьей стороны.

Докажите, что в равнобедренном треугольнике медианы, проведенные к боковым сторонам, равны?

Докажите, что в равнобедренном треугольнике медианы, проведенные к боковым сторонам, равны.

Докажите, что медианы, проведенные к боковым сторонам равнобедренного треугольника, равны?

Докажите, что медианы, проведенные к боковым сторонам равнобедренного треугольника, равны.

Боковая сторона равнобедренного треугольника равна √13см, а основание 4 см?

Боковая сторона равнобедренного треугольника равна √13см, а основание 4 см.

Найдите длину медианы проведенной к основанию.

Помогииите?

Докажите, что медианы равнобедренного треугольника проведенные к боковым сторонам равны.

47 БАЛЛОВ?

Докажите, что если основание и медиана, проведенная к боковой стороне одного равнобедренного треугольника, равны основанию и медиане, проведенной к боковой стороне другого равнобедренного треугольника, то эти треугольники равны.

Заранее огромное спасибо.

Докажите, что медианы проведенные к боковым сторонам равнобедренного треугольника равны?

Докажите, что медианы проведенные к боковым сторонам равнобедренного треугольника равны.

Найдите длину боковой стороны треугольника.

В равнобедренном треугольнике длина основания равна 4, а медианы, проведенные к боковым сторонам, взаимно перпендикулярны?

В равнобедренном треугольнике длина основания равна 4, а медианы, проведенные к боковым сторонам, взаимно перпендикулярны.

Найти площадь треугольника.

Докажите, что в равнобедренном треугольнике медианы, проведенные к боковым сторонам равны?

Докажите, что в равнобедренном треугольнике медианы, проведенные к боковым сторонам равны.

Пусть х см меньшая сторона, тогда 3х большая. Р = 2 * (х + 3х) = 32 4х = 32 : 2 4х = 16 х = 16 : 4 х = 4 4 см меньшая сторона 3 * 4 = 12 (см) большая сторона ответ : 12 см.

Тимур, Женя, Ольга, доктор, молочница, Мишка Квакин, Гейка, Георгий Гараев Вроде всё! : 3.

Источник

Задачи на доказательство геометрических фактов из ГИА

Предлагаю на этот раз устроить что-то вроде «доказательного марафона» по решению задач, которые предлагаются девятиклассникам в вариантах ГИА по математике. Связаны они с доказательством несложных, но в то же время очень полезных геометрических фактов. В статье намеренно не приведены подробные решения задач, лишь некоторые наброски и подсказки. Постарайтесь преодолеть эту марафонскую дистанцию самостоятельно, без ошибок и за один подход.

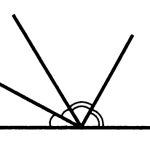
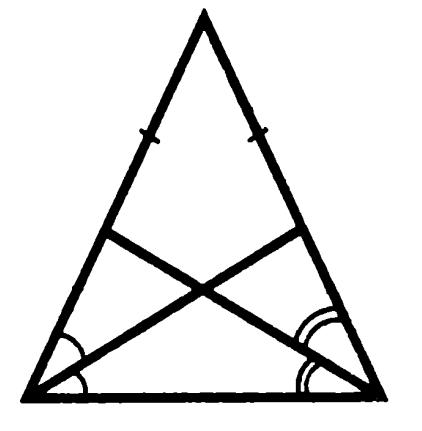
Задача 1. Докажите, что биссектрисы смежных углов перпендикулярны.

Угол α обозначен одной дугой, β — двумя

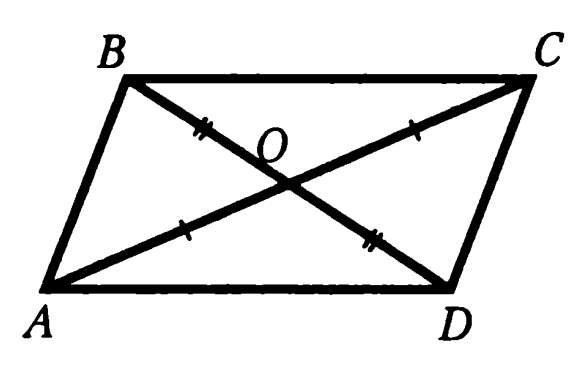
Задача 2. Два отрезка AC и BD пересекаются в точке O, которая является серединой каждого из них. Докажите равенство треугольников ACD и CAB.

ABCD, конечно, будет параллелограммом, но в условии этого не дано

Доказательство: боковые треугольники равны по двум сторонам и углу между ними (BO = OD — по условию, AO = OC — по условию, ∠DOC = ∠AOB — вертикальные), то есть ∠ACD = ∠CAB, а поскольку они являются накрест лежащими при прямых AB, CD и секущей AC, то AB параллельна DC. Аналогично доказываем параллельность прямых BC и AD. Итак, ABCD — параллелограмм по определению. BC = AD, AB = CD (в параллелограмме противоположные стороны равны), AC — общая для треугольников ACD и CAB, поэтому они равны по трем сторонам. Что и требовалось доказать.

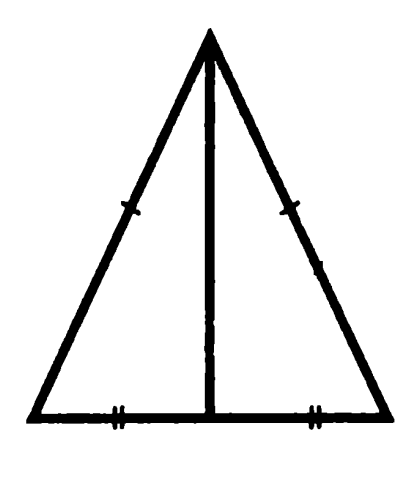
Задача 3. Докажите, что медиана, проведенная к основанию равнобедренного треугольника, является биссектрисой угла, противолежащего основанию, а также перпендикулярна основанию.

Углы, образованные медианой и основанием, назовем «нижними», медианой и боковыми сторонами — «верхними»

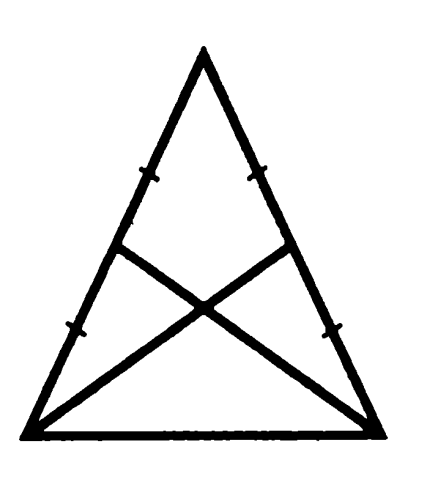
Задача 4. Докажите, что медианы, проведенные к боковым сторонам равнобедренного треугольника, равны.

Треугольники, образованные медианами, основанием и нижними половинами боковых сторон исходного треугольника, назовем «нижними»

Доказательство: углы при основании равнобедренного треугольника равны, поэтому «нижние» треугольники равны по двум сторонам и углу между ними, из чего следует равенство проведенных медиан. Что и требовалось доказать.

Задача 5. Докажите, что биссектрисы, проведенные из вершин основания равнобедренного треугольника, равны.

Все отмеченные на рисунке углы, конечно, равны, хоть и обозначены разными дугами

Доказательство: «нижний» треугольник равнобедренный, что следует из равенства углов при его основании, «боковые» треугольники равны по стороне (равные из доказанного выше частички биссектрис) и двум углам (первые равны по условию, вторые как вертикальные), поэтому оставшиеся частички биссектрис также равны друг другу, а значит равны и сами биссектрисы целиком. Что и требовалось доказать.

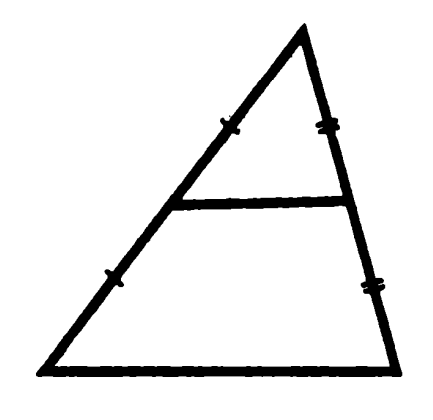
Задача 6. Докажите, что длина отрезка, соединяющего середины двух сторон треугольника, равна половине третьей стороны.

Чистенькие стороны назовем «основаниями», перечеркнутые — «боковыми сторонами»

Доказательство: боковые стороны маленького и большого треугольника на рисунке относятся как 1 : 2, кроме того у них есть один общий угол, а значит они подобны по второму признаку с коэффициентом подобия 1 : 2, поэтому и основания относятся как 1 : 2. Что и требовалось доказать.

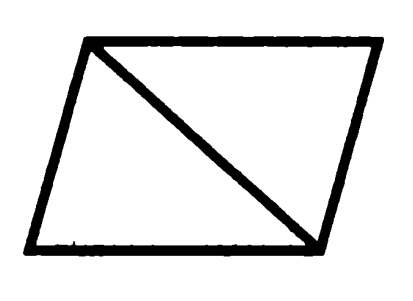
Задача 7. Докажите, что диагональ параллелограмма разбивает его на два равных треугольника.

Параллелограмм с диагональю, больше, пожалуй, добавить нечего

Доказательство: противоположные стороны параллелограмма равны, диагональ является общей стороной для этих треугольников, поэтому они равны по трем сторонам. Что и требовалось доказать.

Задача 8. Докажите, что медиана, прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.

Другими словами медиана проведена из вершины прямого угла

Доказательство: если вокруг данного прямоугольного треугольника описать окружность, то вписанный в эту окружность прямой угол треугольника будет описаться на полуокружность, поэтому гипотенуза будет диаметром этой окружности, а половинки гипотенузы и данная нам в задаче медиана — радиусами, итак, все они равны. Что и требовалось доказать.

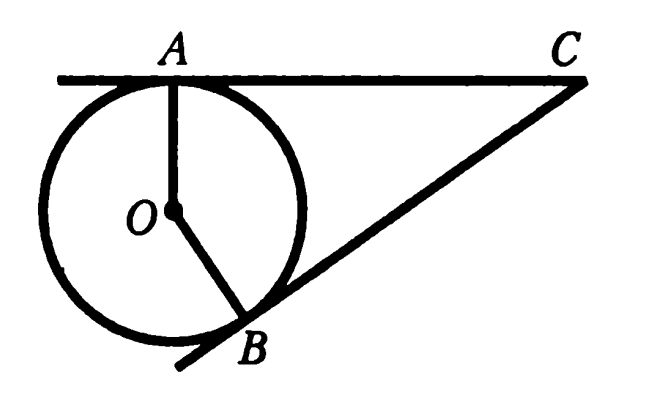
Задача 9. Докажите, что отрезки касательных, проведенных к окружности из одной точки, равны.

Дополнительное построение: соединяем точку C с точкой O (мысленно)

Доказательство: углы B и A прямые (радиусы окружности, проведенные в точку качания, перпендикулярны касательным), значит прямоугольные треугольники AOC и BOC равны по гипотенузе (общая для них воображаемая нами сторона OC) и катету (радиусы окружности OB = OA), а значит AC = CB. Что и требовалось доказать.

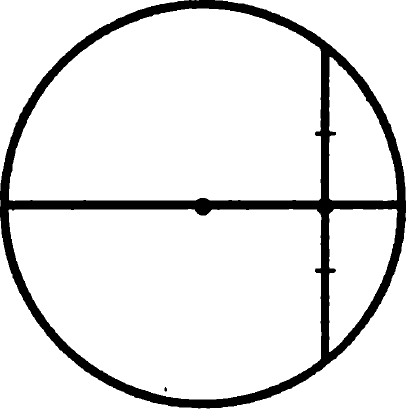
Задача 10. Докажите, что диаметр, проходящий через середину хорды окружности, перпендикулярен ей.

Линия, соединяющая две точки на рисунке, является медианой треугольника, который мы рассмотрим

Доказательство: в равнобедренном треугольнике, образованном точками пересечения хорды с окружностью и центром этой окружности, изображенная медиана будет являться высотой, а значит диаметр, содержащий в себе эту высоту, перпендикулярен хорде. Что и требовалось доказать.

Задача 11. Докажите, что если две окружности имеют общую хорду, то прямая, проходящая через центр этих окружностей, перпендикулярна данной хорде.

Мысленно соединяем вместе все отмеченные на рисунке точки, точку пересечения горизонтали и вертикали назовем H

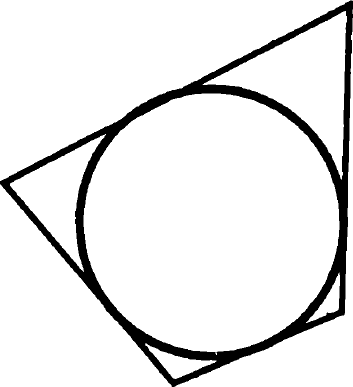
Задача 12. Докажите, что если в четырехугольник можно вписать окружность, то суммы длин его противоположных сторон равны.

Описанный четырехугольник. Назовем его ABCD. Пусть M, E, X и L — точки касания

Доказательство: используем теорему об отрезках касательных (задача 9). ВК = ВР, СР = СН, DX = DL и АТ = АК. Суммируем стороны АВ и CD: AB + CD = (AM + MB) + (DX + XC) = AL + BE + DL + CE = (AL + LD) + (BE + EC) = AD + BC. Что и требовалось доказать.

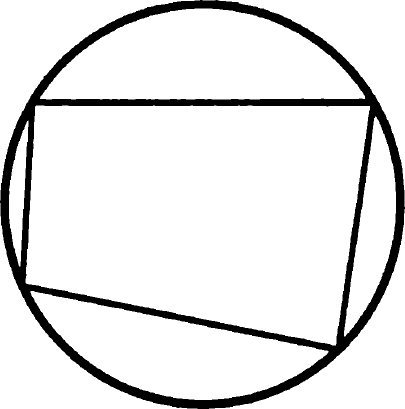
Задача 13. Докажите, что если около четырехугольника можно описать окружность, то суммы его противолежащих углов равны.

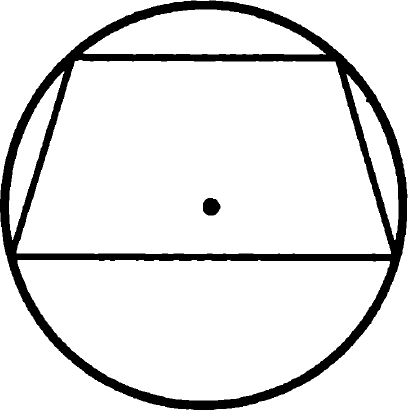
Задача 14. Докажите, что если около трапеции можно описать окружность, то трапеция равнобедренная.

Равнобедренная трапеция, вписанная в окружность

Доказательство: сумма противолежащих углов четырехугольника, вписанного в окружность, равна α + β = 180 0 (см. задачу 13), сумма углов при боковой стороне трапеции также равна α + γ = 180 0 (эти углы являются односторонними при параллельных основаниях и секущей боковой стороне), из сравнения этих формул получаем, что β = γ, то есть углы при основании такой трапеции равны, и она действительно равнобедренная. Что и требовалось доказать.

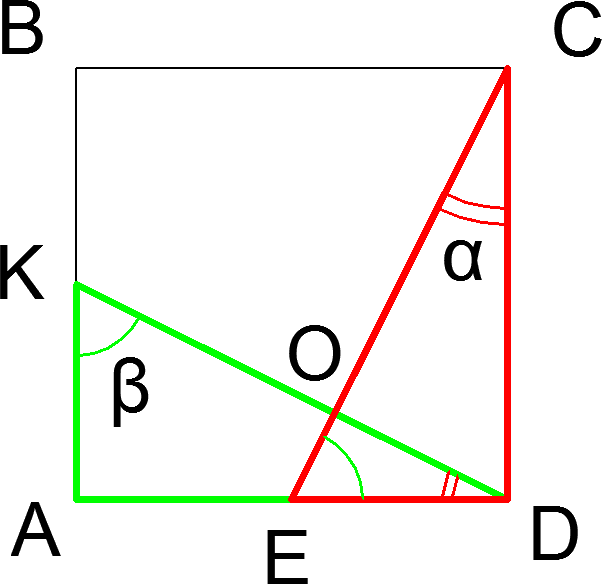
Задача 15. В квадрате ABCD точки К и Е — середины сторон АВ и AD соответственно. Доказать, что КD перпендикулярна CE.

Доказательство. Прямоугольные треугольники AKD и ECD равны по двум катетам, поэтому равны и все их элементы. Пусть

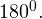
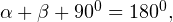
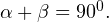
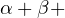
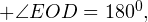
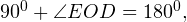
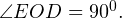
Сумма углов в треугольнике равна Тогда, например, для треугольника AKD имеем а значит Для треугольника EOD имеем то есть а значит Что и доказывает перпендикулярность KD и CE.

Доказанные геометрические факты очень важны, их знание будет вам хорошим подспорьем в решении более сложных задач по геометрии, в первую очередь заданий C4 из вариантов ЕГЭ по математике. Изложенные здесь пояснения эталонными решениями, которые нужно приводить на экзамене, конечно, не являются. Это лишь указатели, используя которые, читатель сможет найти решение самостоятельно.

В любом случае умение решать задачи по геометрии является неотъемлемым условием получения высоких баллов на ЕГЭ и ГИА по математике, что будет гарантией поступления во многие престижные вузы. Успехов вам в подготовке к ГИА и ЕГЭ, талантливых наставников и удачи на экзамене! Ваш репетитор по геометрии Сергей Валерьевич.

Понравилась статья? Возможно, это будет вам интересно:

Источник

1докажите что медиана проведенная к основанию равнобедренного треугольника перпендикулярна основанию 2докажите что медиана проведенные к боковым

сторонам равнобедренного треугольника равны. 3Докажите, что длина отрезка, соед. середины двух сторон рреугольника равна половине длины третьей стороны

Другие вопросы из категории

А) 40 гр
Б) 20 гр
В) 50 гр

Читайте также

касается окружности с центром С и радиусом, равным AD.

3о. Высота, проведенная к основанию равнобедренного треугольника, равно 9см, а само основание равно 24см. Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.

3. Докажите, что в равнобедренном треугольнике биссектриса, проведеная к основанию, делит треугольник на два равных треугольника.

2. Высота, проведенная из вершины равнобедренного треугольника, равна 6, основание треугольника равно 8. Найдите длину боковой стороны?
3. Радиус окружности равен 12 см, найдите длину хорды, которая находится на расстояние 6 см от центра окружности?
4. Высота равностороннего треугольника равна 3, найдите длину его стороны?
5. Боковая сторона равнобедренного треугольника равна 26, угол при основании равен тридцати градусам, найдите длину основания?
6. Стороны прямоугольника 9 см и 12 см. Найдите диагонали прямоугольника?
7. Периметр ромба равен 20 см, одна из его диагоналей равна 8 см. Найдите вторую диагональ ромба?
Ответьте пожалуйста побыстрее.

2.В равнобедренном треугольнике АВС на основании АС лежат точки О и К, причём угол АВО = углу СВК. Докажите, что треугольник АВО и СВК равны.
3.Найдите стороны равнобедренного треугольника, если его периметр равен 10см, а боковая сторона на 2см больше основания.

основание равнобедренного треугольника равно 10 см,а каждая из боковых сторон-7 см.Найдите периметр треугольника

Источник

Определение и свойства медианы в равнобедренном треугольнике

В данной статье мы рассмотрим определение и свойства медиан, проведенных к основанию и боковым сторонам равнобедренного треугольника, а также разберем пример решения задачи для закрепления теоретического материала.

Определение медианы

Медианой называется отрезок в треугольнике, который соединяет вершину и середину противоположной стороны.

Треугольник является равнобедренным, если две его стороны равны (боковые), а третья сторона – это основание фигуры.

Свойства медианы в равнобедренном треугольнике

Свойство 1

Медиана в равнобедренном треугольнике, проведенная к основанию, одновременно является высотой, опущенной на основание, и биссектрисой угла, из которого она проведена.

Свойство 2

В равнобедренном треугольнике медианы пресекаются в одной точке (центр тяжести) и делятся в этой точке в отношении 2:1.

Свойство 3

Медиана делит равнобедренный треугольник на 2 равных по площади (равновеликих) треугольника. Следовательно, S₁ = S₂.

Свойство 4

Если провести три медианы в равнобедренном треугольнике, образуются 6 равновеликих треугольников (S₁ = S₂ = S₃ = S₄ = S₅ = S₆).

Свойство 5

Длину медианы в равнобедренном треугольнике, проведенную к основанию, можно найти по следующей формуле:

Свойство 6

Данной свойство, в отличие от перечисленных выше, не относится к медиане, опущенной на основание фигуры. Оно гласит:

Медианы, проведенные к боковым сторонам равнобедренного треугольника, равны между собой.

AF = CE, следовательно, AE = EB = BF = FC.

Пример задачи

Основание равнобедренного треугольника равняется 7 см, а боковая сторона – 12 см. Найдите длину медианы, проведенной к основанию фигуры.

Решение
Воспользуемся формулой, представленной в Свойстве 5, подставив в нее известные нам по условиям задачи значения:

Источник

Равнобедренный треугольник: свойства, признаки и формулы

Определение равнобедренного треугольника

Какой треугольник называется равнобедренным?

Давайте посмотрим на такой треугольник:

На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.

А вот как называются стороны равнобедренного треугольника:

AB и BC — боковые стороны,

AC — основание треугольника.

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!

Для доказательства следующих теорем нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.

Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

В каждом из доказательств мы пользуемся признаком равенства треугольников, вот и повод их повторить.

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, AH = HC и BH — медиана.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, AH = HC и BH — медиана.

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.

Не должно вас удивить и то, что сумма углов треугольника равна 180°.

∠B = 180° − 80° − 80° = 20°.

Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.

Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.

А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.

Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.

Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.

Источник