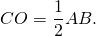Докажите что медиана прямоугольного треугольника проведенная к гипотенузе равна половине гипотенузы

Медиана, проведенная к гипотенузе

Определим и докажем, чему равна медиана прямоугольного треугольника, проведенная к гипотенузе.

Медиана, проведенная к гипотенузе, равна половине гипотенузы.

Доказать: медиана, проведенная к гипотенузе, равна половине гипотенузы.

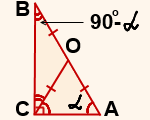
1) В прямоугольном треугольнике АВС из вершины прямого угла С проведем к гипотенузе AB отрезок CO так, чтобы CO=OA.

2) ∆ AOC — равнобедренный с основанием AC (по определению равнобедренного треугольника).

Значит, у него углы при основании равны: ∠ OAC = ∠ OCA=α.

3) Так как сумма острых углов прямоугольного треугольника равна 90º, то в треугольнике ABC ∠ B=90º- α.

4) Так как ∠ BCA=90º (по условию), то ∠ BCO=90º- ∠ OCA=90º-α.

5) Рассмотрим треугольник BOC.

∠ BCO=90º-α, ∠ B=90º- α, следовательно, ∠ BCO= ∠ B.

Значит, треугольник BOC — равнобедренный с основанием BC (по признаку равнобедренного треугольника).

6) Так как CO=OA (по построению) и BO=CO (по доказанному), то CO=OA=BO, AB=OA+BO=2∙OA=2∙CO.

Таким образом, точка O — середина гипотенузы AB, отрезок CO соединяет вершину треугольника с серединой противолежащей стороны, значит, CO — медиана, проведенная к гипотенузе, и она равна половине гипотенузы:

Что и требовалось доказать.

Этот способ может быть использован для доказательства свойства медианы прямоугольного треугольника в 7 классе, поскольку опирается только на материал, уже знакомый к моменту изучения данной темы.

Еще один способ доказательства свойства медианы, проведенной к гипотенузе, рассмотрим в следующий раз.

Источник

Определение и свойства медианы прямоугольного треугольника

В данной статье мы рассмотрим определение и свойства медианы прямоугольного треугольника, проведенной к гипотенузе. Также разберем пример решения задачи для закрепления теоретического материала.

Определение медианы прямоугольного треугольника

Медиана – это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Прямоугольный треугольник – это треугольник, в котором один из углов является прямым (90°), а два остальных – острыми ( Свойства медианы прямоугольного треугольника

Свойство 1

Медиана (AD) в прямоугольном треугольнике, проведенная из вершины прямого угла (∠BAC) к гипотенузе (BC), равна половине гипотенузы.

Следствие: Если медиана равняется половине стороны, к которой она проведена, то данная сторона является гипотенузой, а треугольник – прямоугольным.

Свойство 2

Медиана, проведенная к гипотенузе прямоугольного треугольника, равняется половине квадратного корня из суммы квадратов катетов.

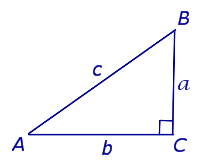
Для нашего треугольника (см. рисунок выше):

Это следует из теоремы Пифагора и Свойства 1.

Свойство 3

Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу описанной вокруг треугольника окружности.

Т.е. BO – это одновременно и медиана, и радиус.

Примечание: К прямоугольному треугольнику также применимы общие свойства медианы, независимо от вида треугольника.

Пример задачи

Длина медианы, проведенной в гипотенузе прямоугольного треугольника, составляет 10 см. А один из катетов равен 12 см. Найдите периметр треугольника.

Решение
Гипотенуза треугольника, как следует из Свойства 1, в два раза больше медианы. Т.е. она равняется: 10 см ⋅ 2 = 20 см.

Воспользовавшись теоремой Пифагора находим длину второго катета (примем его за “b”, известный катет – за “a”, гипотенузу – за “с”):
b 2 = с 2 – a 2 = 20 2 – 12 2 = 256.
Следовательно, b = 16 см.

Теперь мы знаем длины всех сторон и можем посчитать периметр фигуры:
P_△ = 12 см + 16 см + 20 см = 48 см.

Источник

Медиана равна половине гипотенузы

Здравствуйте!
Нужно доказать, что в прямоугольном треугольнике медиана равна половине гипотенузы, к которой проведена.
Спасибо!

Теорема.
Медиана в прямоугольном треугольнике, которая проведена к гипотенузе, равна половине его гипотенузы.

Докажем данную теорему.

Доказательство.
Построим прямоугольный треугольник АВС с прямым углом АСВ.
Проведем в нем медиану CD из прямого угла к стороне АВ. Согласно свойству медианы получим, что отрезок BD равен отрезку AD.
Докажем, что медиана CD равна половине гипотенузы АВ.
Достроим медиану CD так, что отрезок DM будет равен CD. В результате получим четырехугольник AMBC.
Для начала докажем, что полученный четырехугольник АМВС является прямоугольником.
Рассмотрим треугольники ADM и CDВ. Они равны, так как отрезки AD и AB равны, а также отрезки MD и CD равны, а углы между этими сторонами равны как вертикальные. Поскольку эти треугольники равны (по двум сторонам и углу между ними), то их стороны АМ и ВС также равны.
Если аналогично рассмотреть треугольники ADC и BDM, то они также равны, а соответственно их стороны АС и ВМ равны.
Из этого следует, что четырехугольник АМВС является прямоугольником.
По свойству диагоналей прямоугольника, их диагонали пересекаются в точке, которой делятся пополам. Поэтому, можно утверждать, что отрезок CD равен половине отрезка АВ.
Таким образом, мы доказали, что медиана прямоугольного треугольника, проведенная из прямого угла, равна половине его гипотенузы.
Доказательство завершено.

Источник

Медиана в прямоугольном треугольнике

Треугольник называется прямоугольным, если у него есть прямой угол.

Пря­мо­уголь­ный тре­уголь­ник – част­ный слу­чай обыч­но­го тре­уголь­ни­ка. По­это­му все свой­ства обыч­ных тре­уголь­ни­ков для пря­мо­уголь­ных со­хра­ня­ют­ся. Но есть и неко­то­рые част­ные свой­ства, обу­слов­лен­ные на­ли­чи­ем пря­мо­го угла.

Свойство 1. Сумма двух острых углов прямоугольного треугольника равна 90°.

Доказательство: В самом деле, сумма углов любого треугольника равна 180°, а прямой угол равен 90° (∠ C = 90°), поэтому сумма двух острых углов прямоугольного треугольника равна 90°( ∠ А + ∠ В = 180° — 90° = 90°)

Свойство 2. В прямоугольном треугольнике гипотенуза больше любого из катетов (является самой большой стороной).

Так как угол треугольника не может равняться 0, то каждый из них меньше 90°. Значит ∠ C = 90°, является самым большим, а, значит, напротив него лежит наибольшая сторона треугольника.

Значит, гипотенуза является наибольшей стороной прямоугольного треугольника, то есть: с > a и c > b

Свойство 3. В прямоугольном треугольнике гипотенуза меньше суммы катетов.

Доказательство. Это свойство становится очевидным, если вспомнить неравенство треугольника.

Неравенство треугольника «В любом треугольнике сумма любых двух сторон больше третьей стороны»

Из данного неравенства сразу же следует свойство 3. Примечание: несмотря на то, что каждый из катетов по отдельности меньше гипотенузы, их сумма оказывается больше

Дано: Δ ABС — прямоугольный треугольник

Значит, прямоугольные треугольники Δ ABС = Δ AСD (по двум катетам: AC– общий, BC и CD– по построению) – первый признак равенства прямоугольных треугольников.

Значит, треугольник – равнобедренный (так как у него равны углы при основании), но равнобедренный треугольник, один из углов которого равен 60° – равносторонний.

Из этого следует, в частности, что AB = 2ВС

Если в треугольнике медиана равна половине стороны, к которой она проведена, то данный треугольник является прямоугольным, причём медиана проведена из вершины прямого угла.

Признаки равенства прямоугольных треугольников

Читатели сайта «Спиши у Антошки уже прочитали «Признаки равенства треугольников». Естественно, все эти признаки остаются верными и для прямоугольных треугольников.

Однако у прямоугольных треугольников есть одна существенная особенность – у них всегда есть пара равных прямых углов. Поэтому данные признаки для них упрощаются.

Итак, сформулируем признаки равенства прямоугольных треугольников:

Прямоугольные треугольники равны если у них равны:

. — два катета;

Доказательство: в прямоугольных треугольниках:Δ ABС и Δ A1B1С1 ∠ C = 90° = ∠ C1. Значит, мы можем воспользоваться первым признаком равенства треугольников (по 2 сторонам и углу между ними) и получить: Δ ABС = Δ A1B1С1.

— катет и прилежащий острый угол;

«Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны»

Доказательство: сразу отметим, что тот факт, что равны углы, прилежащие к равным катетам, не является принципиальным. Действительно, сумма острых углов прямоугольного треугольника (по свойству 1) равна 90°. Значит, если равна одна пара из этих углов, то равна и другая (так как их суммы одинаковы).

Доказательство же данного признака сводится к использованию второго признака равенства треугольников (по 2 углам и стороне). Действительно, по условию равны катеты и пара прилежащих к ним углов. Но вторая пара прилежащих к ним углов состоит из углов ∠ C = 90° = ∠ C1. Значит, мы можем воспользоваться вторым признаком равенства треугольников и получить: Δ ABС = Δ A1B1С1.

— гипотенуза и острый угол.

«Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны»

«Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны»

Дано: Δ ABС и Δ A1B1С1

Доказать, что Δ ABС = Δ A1B1С1

Доказательство: для доказательства этого признака воспользуемся признаком равенства треугольников, который мы сформулировали и доказали на прошлом уроке, а именно: если у треугольников равны две стороны и больший угол, то такие треугольники являются равными.

Действительно, по условию у нас есть две равных стороны. Кроме того, по свойству прямоугольных треугольников: ∠ C = 90° = ∠ C1. Осталось доказать, что прямой угол является наибольшим в треугольнике.

Значит, прямой угол является наибольшим в прямоугольным треугольнике. А значит, можно воспользоваться сформулированным выше признаком, и получить:Δ ABС = Δ A1B1С1.

Геометрия. Урок 3. Задания. Часть 2

Решение:

Решение:

Решение:

Решение:

№14. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 12 и 13.

Решение:

Решение:

В △ A B C два угла равны, значит он равнобедренный.

№16. На рисунке изображён прямоугольный треугольник. Найдите длину медианы треугольника, проведённую из вершины прямого угла.

Решение:

В прямоугольном треугольнике медиана, проведенная из вершины прямого угла равна половине гипотенузы.

Решение:

Решение:

Свойства медианы в прямоугольном треугольнике с доказательствами

В этой статье мы рассмотрим свойства медианы в прямоугольном треугольнике, а также их доказательства.

Медиана — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Для прямоугольного треугольника это будут медианы, проведённые с острого угла к серединам катетов или с прямого к центру гипотенузы (рис. 1).

Свойства медианы в прямоугольном треугольнике

Доказательства свойств

Первое свойство

Доказать, что медианы в прямоугольном треугольнике пересекаются в одной точке и делятся в пропорции 2:1, считая от вершины.

Доказательство:

Что и требовалось доказать.

Второе свойство

Доказать, что медиана, проведённая с вершины прямого угла к гипотенузе, равна половине гипотенузы.

Доказательство:

Что и требовалось доказать.

Третье свойство

Доказать, что медиана, проведённая к гипотенузе прямоугольного треугольника, является радиусом описанной окружности.

Доказательство:

Источник

Свойства прямоугольного треугольника

Катеты прямоугольного треугольника

Длины катетов прямоугольного треугольника меньше длины гипотенузы.

Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты.
Острые углы равнобедренного прямоугольного треугольника равны 45°.

Катет, равный половине гипотенузы

Медиана, проведённая к гипотенузе прямоугольного треугольника

Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.

Медиана треугольника, равная половине стороны, к которой она проведена

Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным.

Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности.

Если в треугольнике центр описанной окружности лежит на одной из сторон, то этот треугольник является прямоугольным треугольником, а центр описанной окружности совпадает с серединой гипотенузы.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Обратная теорема Пифагора

Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным

Определение прямоугольного треугольника:

Свойство катетов прямоугольного треугольника:

Длины катетов прямоугольного треугольника меньше длины гипотенузы.

Равнобедренный прямоугольный треугольник

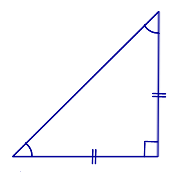
Определение равнобедренного прямоугольного треугольника:

Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты.

Свойство углов прямоугольного треугольника:

Прямоугольный треугольник с углом в 30°

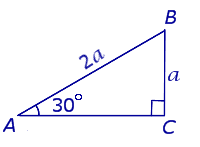
Свойство прямоугольного треугольника с углом в 30° :

Признак прямоугольного треугольника с углом в 30° :

Медиана, проведённая к гипотенузе прямоугольного треугольника

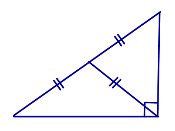
Свойство медианы, проведенной к гипотенузе прямоугольного треугольника:

Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.

Признак прямоугольного треугольника:

Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным.

Центр описанной окружности

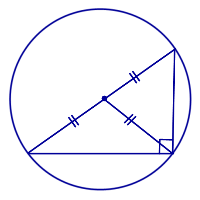
Свойство окружности, описанной около прямоугольного треугольника:

Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности.

Признак прямоугольного треугольника:

Если в треугольнике центр описанной окружности лежит на одной из сторон, то этот треугольник является прямоугольным треугольником, а центр описанной окружности совпадает с серединой гипотенузы.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Обратная теорема Пифагора:

Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным

Источник