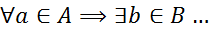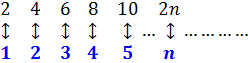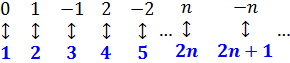Докажите что множество чисел вида 1 3k где k принадлежит n счетно
Математический портал
Nav view search
Navigation
Search
Счетность и несчетность множеств. Равномощность множеств.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Примеры.
Доказать, что следующие множества счетны:
Решение.
Что и требовалось доказать.
Решение.
Что и требовалось доказать.
Решение.
Что и требовалось доказать.
Решение.
Что и требовалось доказать.
Примеры:
Доказательство.
Что и требовалось доказать.
Доказательство.
Проведем доказательство в несколько этапов:
Что и требовалось доказать.
Домашнее задание.
Доказать, что следующие множества счетны:
1.70. Используя результат задачи 1.68, доказать, что множество всех точек плскости с рациональными координатами счетно.
Множество всех действительных чисел не счетно. Г. Кантор
И тем не менее несчетные множества существуют. Оказывается, множество всех действительных чисел — не счетно. Этот замечательный факт, как и теорема о счетности множества всех рациональных чисел, впервые в 1874 г. был доказан знаменитым немецким математиком Г. Кантором, основателем современной теории множеств.
Воспроизводим доказательство Кантора. Доказываем, что несчетным является уже множество всех действительных чисел интервала 1 (0; 1).
Каждое такое действительное число может быть записано в виде бесконечной десятичной дроби с целой частью нуль. При этом каждому действительному числу соответствует лишь одна такая запись, за исключением действительных чисел, выражаемых конечными десятичными дробями: каждое такое число, например 0,2476622021711, может быть записано двумя способами в виде бесконечной десятичной дроби:
Одна из этих записей начиная с некоторого момента содержит одни лишь нули, а другая— одни девятки. Если мы согласимся не употреблять записей, в которых, начиная с какого-нибудь места, идут одни девятки, то каждое действительное число будет иметь лишь единственную запись в виде бесконечной десятичной дроби. Докажем теперь теорему о несчетности множества действительных чисел от противного: предположим, что множество действительных чисел [мы говорим все время о числах X интервала (0 ; 1)] счетно, т.е. может быть занумеровано посредством натуральных чисел. Тогда вся совокупность действительных чисел интервала (0 ; 1) может быть записана в виде последовательности: х1, х2. Запишем разложение числа xn в бесконечную десятичную дробь в виде:
суть последовательные десятичные знаки числа xn, причем, согласно заключенному нами условию, не может случиться, что все десятичные знаки начиная с некоторого суть девятки. Итак, все действительные числа х [интервала (0; 1)] предполагаются записанными в виде:
Табл: I
Приведем наше предположение к противоречию, найдя действительное число с, заключенное между 0 и 1 и заведомо не входящее в табл. I. Для этого рассмотрим цифры, стоящие по диагонали в табл. I, а именно:

и выберем для каждого n натуральное число bn, не превосходящее число 8 и отличное от числа a ( n) n (например, при а ( n) n (n) n=8 полагаем bn=7). Рассмотрим бесконечную десятичную дробь
то на n-м месте в разложении числа с мы должны были бы иметь цифру
тогда как действительно имеем
1 Под интервалом (а; b) числовой прямой понимается множество всех действительных чисел х, удовлетворяющих неравенству а
06. Теоремы о счетных множествах. Множества мощности континуум
Если рассмотреть любое конечное множество и любое его собственное (непустое и не совпадающее с ним самим) подмножество, то элементов в подмножестве меньше, чем в сам множестве, т. е. часть меньше целого.
Обладают ли бесконечные множества таким свойством? И может ли иметь смысл утверждение, что в одном бесконечном множестве «меньше» элементов, чем в другом, тоже бесконечном? Ведь про два бесконечных множества мы можем пока только сказать, эквивалентны они или нет. А существуют ли вообще неэквивалентные бесконечные множества?
Приведём забавную фантастическую историю из книги Н. Я. Виленкина «Рассказы о множествах». Действие происходит в далёком будущем, когда жители разных галактик могут встречаться друг с другом. Поэтому для всех путешествующих по космосу построена огромная гостиница, протянувшаяся через несколько галактик.
В этой гостинице бесконечно много номеров (комнат), но, как и положено, все комнаты пронумерованы, и для любого Натурального числа n есть комната с этим номером.
Однажды в этой гостинице проходил съезд космозоологов, в котором участвовали представители всех галактик. Так как галактик тоже бесконечное множество, все места в гостинице оказались занятыми. Но в это время к директору гостиницы приехал его друг и попросил поселить его в эту гостиницу.
«После некоторых размышлений директор обратился к администратору и сказал:
– Куда же я дену жильца этого номера? – удивлённо спросил администратор.
– А его переселите в № 2. Жильца же из № 2 отправьте в № 3, из № 3 – в № 4 и т. д.»
Вообще, пусть постоялец, живущий в номере K, переедет в номер K+1, как это показано на следующем рисунке:
Тогда у каждого снова будет свой номер, а № 1 освободится.
Таким образом, нового гостя удалось поселить – именно потому, что номеров в гостинице бесконечно много.
Первоначально участники съезда занимали все номера гостиницы, следовательно, между множеством космозоологов и множеством N Было установлено взаимно однозначное соответствие: каждому космозоологу дали по номеру, на двери которого написано соответствующее ему натуральное число. Естественно считать, что делегатов было «столько же», сколько имеется натуральных чисел. Но приехал ещё один человек, его тоже поселили, и количество проживающих увеличилось на 1. Но их снова осталось «столько же», сколько и натуральных чисел: ведь все поместились в гостиницу!
Мы пришли к удивительному выводу: если к множеству, которое равномощно N, добавить ещё один элемент, получится множество, которое снова равномощно N. Но ведь совершенно ясно, что делегаты-космозоологи представляют собой часть того множества людей, которые разместились в гостинице после приезда нового гостя. Значит, в этом случае часть не «меньше» целого, а «равна» целому!
Итак, из определения эквивалентности (которое не приводит ни к каким странностям в случае конечных множеств) следует, что часть бесконечного множества может быть эквивалентна всему множеству.
Новый постоялец не удивился, когда на другое утро ему предложили переселиться в № 1000000. Просто в гостиницу прибыли запоздавшие космозоологи из галактики ВСК-3472, и надо было разместить ещё 999999 жильцов.
Эта задача оказалась весьма сложной. Но и в этом случае нашёлся выход.
«В первую очередь администратор приказал переселить жильца из № 1 в № 2.
– А жильца из № 2 переселите в № 4, из № 3 – в № 6, вообще, из номера N – в номер 2n.
Определение. Множество А, равномощное множеству натуральных чисел N, называется Счетным множеством (имеет мощность счетного множества). Если множество В является бесконечным и не равномощно множеству N, то его называют несчетным.
Множество, которое является конечным или счетным, еще называют не более чем счетным .
Пусть множество А является счетным. По определению, тогда существует биекция А на N, т. е. каждому аÎА соответствует единственный номер nÎN и множество А обращается в некоторую последовательность <аn>.
Теорема 1. Любое подмножество счетного множества не более чем счетно.
Доказательство. Пусть А = 

Теорема 2. Объединение конечного или счетного числа счетных множеств является счетным множеством.
Теорема 3. Любое бесконечное множество содержит счетное подмножество.
Доказательство. Выберем в заданном множестве А какой-либо элемент, придав ему единичный индекс: а1. Среди всех оставшихся элементов множества А найдется не равный а1 элемент (в силу бесконечности А). Его мы обозначим через а2. Продолжая этот процесс до бесконечности мы получим необходимое нам счетное множество
Доказательство. Пусть множество М – А не более чем счетно. Тогда множество М = АÈ(М – А) по теореме 2 не более чем счетно. Это противоречит тому, что множество М несчетно и, следовательно, наше исходное предположение не верно. Таким образом, множество М – А несчетно. Последнее еще не означает равномощности множеств М и М – А. Докажем ее. Выделим из М – А счетное множество В. Обозначим через С множество С = (М – А) – В. Справедливы равенства М = АÈВÈС и М – А = ВÈС. Множество АÈВ счетно (теорема 2). Следовательно, существует биекция f из АÈВ на А. Теперь можно построить биекцию g из М на М – А по правилу:
Теорема 5. Если множество С бесконечно, а В не более чем счетно, то множество ВÈС равномощно множеству С.
Доказательство. Если множество С счетно, то множество ВÈС также счетно и следовательно они равномощны. Если же множество С не счетно, то мы можем воспользоваться теоремой 4, положив в ней А = СÇВ, а М = С.
Теорема 6. Если множество С является бесконечным, то существует его подмножество В такое, что В¹С и В равномощно с С.
Доказательство. По теореме 3 мы можем выделить из множества С его счетное подмножество А. Если множество С счетно, то в качестве В из утверждения теоремы можно взять В=А. Если же С не счетно, то можно положить В=С-А и утверждаемое вытекает из теоремы 4.
Теорема 7. Множество рациональных чисел Q является счетным.
Доказательство. Обозначим через Р множество всех пар натуральных чисел (p, q), таких что p и q не имеют общих целых делителей, кроме единицы. Для пары натуральных чисел (p, q) введем ее высоту m = p + q. Обозначим Рn множество пар натуральных чисел высоты n. Нетрудно проверить, что каждое множество Рn является конечным и содержит не более, чем n-1 член. Так как Р = Èn Рn, то множество Р счетно в силу теоремы 2.
Теорема 8. Множество точек интервала (0,1) является несчетным.
Доказательство (Диагональный метод Кантора). Доказательство проведем от противного, предположив, что множество точек интервала (0,1) является счетным. Тогда все точки можно записать в виде последовательности:
Множества, равномощные множеству точек интервала (0, 1), называются множествами мощности Континуум .
Задачи.
1. Показать, что если множества А и В являются счетными, то и их произведение А´В является счетным.
2. Установить биекцию между множеством N всех натуральных чисел и множеством Q всех четных положительных чисел.
3. Установить биекцию между множеством N всех натуральных чисел и множеством Р всех четных чисел.
Что такое счётное множество?
Множеств в математике… великое множество. 🙂 Вот ведь сказанул! Да простит меня русский язык, но иначе и не скажешь. 🙂 Самых-самых разнообразных. 🙂 Бывают числовые множества. Это, как и намекает название, множества, элементами которых являются числа. Бывают множества функций. Например, любой неопределённый интеграл ∫ f(x)dx — это множество функций вида F(x)+C, где С — любая константа. Но не просто функций, а таких, что F’(x) = f(x). Или множество всех слов, составленных из определённого набора букв. Да много чего можно насочинять. 🙂 Мы пока в данной теме для простоты ограничимся числовыми множествами. С ними как-то попроще в математике работать, чем с остальными видами множеств, правда?
Среди всех множеств (в том числе и числовых) бывают конечные и бесконечные.
С конечными множествами всё просто. Это, как и намекает название, множества с конечным числом элементов. Во множестве может содержаться один элемент, может быть 345 элементов, хоть миллиард. Но — конечное число. Пусть даже очень большое.
Например, если A — множество корней квадратного уравнения x 2 — 3x + 2 = 0, то оно является конечным и состоит всего из двух элементов — чисел 1 и 2:
Или множество всех бактерий на планете Земля. Очень большое, но — тоже конечное.)
Примеры бесконечных множеств вам тоже хорошо знакомы ещё со школы.
N — множество всех натуральных чисел,
Z – множество всех целых чисел,
Q — множество всех рациональных чисел,
R — множество всех действительных чисел.
А теперь приведу более хитрые примеры бесконечных множеств:
— множество всех точек отрезка [0; 1];
— множество всех точек окружности радиуса «R«;
— множество всех точек квадрата со стороной «a«.
На первый (обывательский) взгляд может показаться, что эти три множества вполне себе конечны. И на то есть веские основания. В самом деле, ведь отрезок [0; 1] имеет вполне определённую длину и, по идее, должен «вмещать» в себя лишь некоторое конечное число точек! Окружность и квадрат тоже как-то ограничены по длине/площади и вмещают в себя лишь какое-то конечное число точек!
Но не всё так просто и очевидно, как кажется на первый наивный взгляд. К сожалению… Во всяком случае, для гуманитариев. А вот юные математики, возможно, уже сейчас смогли нутром прочувствовать, почему эти три множества бесконечны. Прочувствовали? Пока нет? Подробности — чуть позже. В соответствующем уроке.
Ну а коли уж мы затронули такое скользкое понятие, как бесконечность, то неплохо было бы о ней немного побеседовать. Пофилософствовать…
Немного о бесконечности…
Бесконечность во все времена привлекала внимание людей. И математиков — особенно.) Термином «бесконечность» мы обычно называем всё, что невозможно сосчитать или перечислить. Бесконечность в нашем воображении — это что-то запредельное, невообразимо большое. Или напротив, чрезвычайно маленькое, к чему можно стремиться сколь угодно долго, но достичь которого невозможно. Вроде бы всё просто, но… Сможете привести мне пример реально бесконечного объекта?
Первое, что приходит большинству на ум, — это наша Вселенная, состоящая из бесчисленного количества звёзд, планет, молекул, атомов и других частиц. Но на самом деле никто из нас не знает, какая именно наша Вселенная на самом деле — конечная она или бесконечная. Никто из нас не видел её границ. Человеку свойственно не видеть часть того, что происходит, да… И не только человеку. Например, какому-нибудь муравью его муравейник будет казаться примерно тем же самым, что и для нас, скажем, жилой дом. А наша планета в целом для муравья будет казаться такой же бесконечной, как и Вселенная для нас. Муравьи в космос ещё не летали, да.)
Но что такое муравейник, жилой дом и даже вся планета Земля не для муравья, а для нас с вами? В нашем мироощущении и в нашей системе координат? Песчинки! Ну… почти.) Зато для нас, скажем, число 2 100 настолько огромно, что простой перебор всех натуральных чисел, его не превосходящих, даже при помощи самого современного супермощного компьютера, потребует невообразимо много сроков жизни самого компьютера… Тем не менее, эти объекты (муравейник, жилой дом, планета Земля и даже число 2 100 ) — конечны. Это значит, что процесс их «пересчёта» (песчинок в муравейнике, кирпичей в жилом доме и всех натуральных чисел от 1 до 2 100 ) когда-нибудь да закончится. Рано или поздно…
А вот, скажем, множество всех целых чисел — бесконечно! Именно реально бесконечно. Какое бы целое число мы ни взяли, всегда можно перейти к следующему, прибавив к предыдущему единичку. Таким образом, мы никогда не сможем сказать: «Вот! Все целые числа перечислены, и других целых чисел больше нет!»
Как сравнивать бесконечности? Что такое взаимно-однозначное соответствие?
С конечными множествами мы с вами худо-бедно работать умеем — изображать на картинках, объединять, пересекать и т.д. Также их легко сравнивать друг с другом — в каком-то множестве больше элементов, в каком-то — меньше. Пересчитали элементы каждого, сравнили два числа и — дело в шляпе.
А вот как грамотно работать с бесконечными множествами? И, в первую очередь, как правильно сравнивать бесконечные множества? В каком из двух бесконечных множеств больше элементов? И что подразумевается под этим самым «больше»? Пока для нас с вами это всё тайна, покрытая мраком…
Ответы на эти животрепещущие вопросы долгое время искал немецкий математик Георг Кантор (1845 — 1918). Вообще, Германия всегда славилась талантливыми учёными-математиками, чего греха таить! Кто не знает знаменитых Гаусса или Кеплера! А студенты физико-математических специальностей содрогаются от страха, услышав фамилии Вейерштрасс или Риман.) Да и Франция тоже не отставала: Паскаль, Лаплас, Коши, Лагранж, Лежандр, Фурье, Лебег, Лиувилль — все эти фамилии хоть раз были на слуху у любого человека, когда-либо всерьёз занимавшегося математикой.)
Но мы с вами обратимся к Кантору.) Его по праву считают основоположником теории множеств. И не зря! Ведь именно он перевёл часть наших знаний о бесконечности из ощущений в строгую математику!
Прежде всего, он придумал красивый и элегантный способ сравнения бесконечных множеств. Основывается этот интересный способ сравнения множеств на так называемом взаимно-однозначном соответствии. Или взаимно-однозначном отображении. Которое в высшей математике называется красивым словом «биекция». Но мы сейчас не будем изображать из себя «true-математегов», умничать, давать строгие определения и заниматься всякой клинописью типа
Этого добра хватает в любом учебнике по высшей математике. Не для этого разрабатывался этот сайт…
В чём же фокус? Как можно объяснить термин «взаимно-однозначное соответствие» на пальцах? Представим себе ситуацию, что в бесконечных размеров аудиторию входит бесконечное число студентов. Представили?) Всех студентов надо как-то рассадить на стулья. Которых, естественно, тоже будет бесконечное количество.)
Итак. Что же такое взаимно-однозначное соответствие?
Представим себе теперь, что все наши студенты гурьбой вваливаются в эту бесконечную аудиторию и рассаживаются на стулья.
Так вот, при взаимно-однозначном соответствии между множеством студентов (А) и множеством стульев (В) каждый студент сядет на некоторый свой персональный стул! Причём только на один! Более того, в аудитории (да-да, бесконечной!) не останется ни пустующих стульев, ни стоящих студентов. И никому не будет обидно: вся наша бесконечная орава студентов дружно будет сидеть на стульях и слушать увлекательную лекцию про теорию множеств.)
А теперь нарисуем наших студентов и аудиторию со стульями на картинке.
Так вот, математически термин взаимно-однозначное соответствие означает, что каждому элементу из первого множества «А» можно поставить в соответствие один и только один элемент из второго множества «В».
И наоборот, любому элементу множества «B» будет соответствовать некоторый единственный элемент из множества «А». И всё!
На нашей картинке каждый элемент из первого множества (студентов) связан с элементом второго (стульев) только одной стрелочкой. Причём очень важно, что ни в одном из множеств нету элемента без пары! К каждому элементу ведёт своя стрелочка. И притом только одна. А не две или ни одной. И именно эти самые стрелочки и показывают нам, что каждый студент сидит на своём стульчике. И наоборот, у каждого стульчика есть свой персональный хозяин.) Это важно!
Идём дальше. Наш уважаемый Кантор настолько увлёкся идеей взаимно-однозначного соответствия между различными множествами, что начал получать просто потрясные и совершенно неожиданные результаты! И тем самым развеял очень многие мифы, в которые до него исправно верило всё человечество, ссылаясь на пресловутую интуицию… Результаты настолько неожиданные, что у студентов-новичков на данном этапе знакомства с теорией множеств даже теряется вообще доверие к математике. Как вообще такое возможно? Неужели это и вправду не сон?!
Например, сейчас я начну нести ахинею утверждать совершенно немыслимые и противоречащие обычной житейской логике и здравому смыслу факты. И развеивать мифы так, как это сделал Кантор.)
Миф №1: Чётных чисел вдвое меньше, чем натуральных .
Факт: И тех и других одинаковое количество! Более того, натуральных чисел, кратных трём (пяти, десяти, да хоть миллиарду!), столько же, сколько и самих натуральных чисел.
Миф №2: Рациональных чисел гораздо больше, чем натуральных.
Факт: Ничего подобного! Их тоже одинаковое количество! Пускай и бесконечное…
Дальше — больше! Держитесь покрепче и не упадите! Вот вам ещё эпичные факты:
Точек на окружности радиуса 1 столько же , сколько и на окружности радиуса 5. Или радиуса 100. Или любого другого радиуса.
Точек в квадрате со стороной 1 столько же , сколько и на отрезке [0; 1] (и, соответственно, на всей прямой).
Что, неожиданно? Парадокс? Не вяжется с житейской логикой? Поначалу — да. Разгадка этих парадоксов кроется в том, что именно мы хотим подразумевать под понятием «столько же» для бесконечного множества. Кантор дал строгое определение этому понятию.
Бесконечное множество «А» (любое!) содержит СТОЛЬКО ЖЕ элементов, сколько и другое бесконечное множество «В», если между элементами этих множеств можно установить взаимно-однозначное соответствие!
Вот и всё.) И именно поэтому я начал наш урок с объяснения, что же такое взаимно-однозначное соответствие. Понятна эта фраза? Если непонятна, вернитесь чуток назад и снова перечитайте про студентов, сидящих на стульях в бесконечной аудитории.)
Ну что, вот мы плавненько подошли к основной теме нашего урока — понятию счётного множества. Оказывается, среди всего многообразия бесконечных множеств в математике выделяется особый класс множеств — счётные множества. Это очень-очень важное понятие в теории бесконечных множеств. Начнём разбираться. И параллельно доказывать эти, казалось бы, противоестественные в нашем восприятии факты.)
Что же такое счётное множество?
Так что же такое счётное множество? Слово «счётное», очевидно, однокоренное со словами «счёт», «считать». Значит, что-то в таком множестве мы должны считать. ) А считать мы будем его элементы. 🙂
Так вот, говоря по-русски, счётное множество — это такое множество, все элементы которого можно перенумеровать. Или пересчитать. По порядочку. Как цыплят. Ну, не совсем буквально, конечно. 🙂
Если наше рассматриваемое множество конечное (даже если оно очень большое), то вопросов нет: каждому его элементу можно так или иначе присвоить какой-то порядковый номер: какой-то элемент будет первым, какой-то вторым, какой-то сорок пятым и так далее. Пока все элементы не пересчитаем. 🙂
А что делать если множество бесконечно? Разве можно в этом случае взять и пересчитать все-все его элементы? Ведь так и будем считать до посинения…
Оказывается, для некоторых бесконечных множеств пересчитать все их элементы тоже можно! 🙂 Да-да! Как именно? Очень интересно! Нет, конечно же, мы не будем сидеть и кропотливо пересчитывать каждый элемент, как мы это обычно делаем для множеств конечных. Никакой даже самой длинной жизни не хватит. Так как же тогда можно пересчитать ВСЕ элементы БЕСКОНЕЧНОГО множества? Причём быстро! И ни один элемент не забыть!
А вот как. Нужно всего лишь установить правило (или закон), согласно которому каждому элементу данного бесконечного множества можно присвоить (то есть, поставить в соответствие) некоторый порядковый номер «n«.
Бесконечное множество (любое!) является счётным, если можно установить взаимно-однозначное соответствие между каждым его элементом и всеми числами натурального ряда.
Вникли? Под умными словами «установить взаимно-однозначное соответствие между каждым его элементом и всеми числами натурального ряда» как раз и скрывается безобидный глагол «пересчитать». И всё. Никаких хитростей.) Представьте себе, что большая группа туристов собирается в интересный и насыщенный поход по Карелии. Руководитель-гуманитарий скажет: «Народ! Давайте-ка я вас пересчитаю!» А вот руководитель-математик может выпендриться и заявить: «Народ! Замрите! Мне надо установить взаимно-однозначное соответствие между нашей командой и числами натурального ряда!»))).
Так вот, если такое взаимно-однозначное соответствие между элементами множества и натуральными числами (т.е. способ пересчёта) установить можно, то в таких случаях математики говорят, что наше множество счётно. Причём совершенно не важно, как именно мы с вами это самое соответствие (или правило) установили. Хоть формулой, хоть табличкой, хоть картинкой, хоть словами… Главное — установили.)
А вот если нам удалось доказать, что такое соответствие (правило) установить нельзя, то в таком случае математики обычно говорят, что такое множество несчётно. 🙂
Вот так вот. Почувствуйте разницу! Ключевыми словами здесь являются слова «удалось доказать». Они означают, что, если мы с вами как-то докажем, что нужное нам взаимно-однозначное соответствие установить нельзя, то из этого автоматом будет следовать, что рассматриваемое нами множество несчётно.
Но! Если мы с вами, по каким-то причинам, никакого соответствия так и не установили, но при этом ещё и не доказали, что такое соответствие установить невозможно, то из этого факта не будет следовать ни того, ни другого! Ни счётности множества, ни его несчётности. Что правда, то правда. Мало ли? Может, мы с вами какие-то тупые двоечники и просто не смогли поднапрячься и придумать нужное правило, по которому можно было бы осуществить это соответствие?! А, скажем, дядя Вася из деревни Кукуево посидел на лавочке с бутылкой самогона часок-другой — и… эврика! Правило найдено!)
А говоря ещё более строго, научно и кратко, счётное множество – это множество, эквивалентное (или равномощное) множеству натуральных чисел N.
Что означают страшные слова «эквивалентное» и «равномощное», мы подробно разберём чуть позже. Когда разберёмся с таким важным понятием, как мощность множества. И к этому строгому определению ещё обязательно вернёмся.
Посмотрим на счётное множество в жизни?
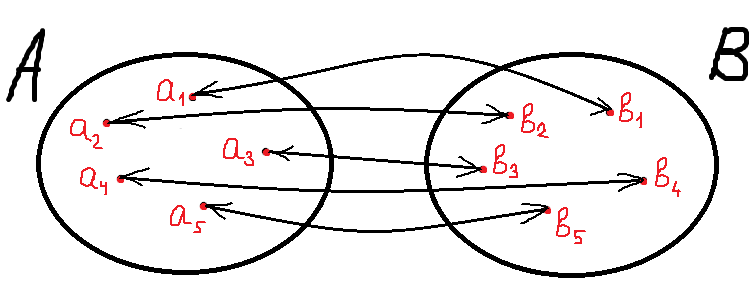
Например, давайте докажем, что множество всех положительных чётных чисел является счётным. Как это сделать? Очень просто. 🙂 Выпишем в ряд первые несколько таких чисел:
Любой ээээ… короче, любой сообразит, что первым таким числом будет двойка, вторым — четвёрка, третьим — шестёрка. И так далее.) Десятым номером пойдёт 20, сотым — 200. И так до бесконечности: каждое чётное число когда-нибудь получит свой заветный номер. А именно — вдвое меньший, чем само это число. 🙂 Вот мы и установили взаимно-однозначное соответствие между чётными числами и их номерами (т.е. ничем иным, как множеством натуральных чисел N!). Незаметно для себя. 🙂
Пожалуйста! Вот оно, это соответствие:
Сюрприз здесь состоит в том, что на бесконечности далеко не всегда работает наш незыблемый постулат, гласящий, что часть меньше целого. И это ещё далеко не все сюрпризы, которые готовит нам теория множеств и работа с бесконечными объектами!) На бесконечности — уже совершенно другая математика… И зачастую идущая вразрез с нашей интуицией, да.)
Какие ещё можно привести примеры счётных множеств? Например, множество элементов любой арифметической или геометрической прогрессии (да и вообще любой числовой последовательности) всегда является счётным. Почему? Да потому, что сама конструкция числовой последовательности подразумевает нумерацию её элементов (т.е. членов)! Есть первый член, есть 37-й, есть 345-й и так далее. 🙂 Все элементы последовательности занумерованы и каждый — на своём месте. 🙂
Счётность множества всех целых чисел Z
А теперь давайте посмотрим, счётно ли множество всех целых чисел Z. Снова, как и чётные числа, попробуем их занумеровать по порядочку. Начнём наш пересчёт с нуля. Число 0 у нас получает почётный номер 1. А вот дальше возникает резонный вопрос — как нам быть с противоположными целыми числами? По какому принципу их нумеровать? Легко! Противоположные числа мы будем выписывать парами — положительное и отрицательное. 🙂 Вот так:
Таким образом, каждое целое число мы рано или поздно выпишем и ни одно не забудем. 🙂
А дальше всё просто — берём и начинаем нумеровать все наши выписанные целые числа по парам! По порядочку. Нолик будет под номером 1, единичка — под номером 2, минус единичка — под номером 3. И так далее. Все положительные числа нумеруем чётными номерами, а все отрицательные — нечётными.
Установили взаимно-однозначное соответствие между целыми числами и натуральным рядом? Конечно! 🙂
Итак, всё доказано! Множество Z — счётно. Вне всяких сомнений. 🙂
Переходим теперь к множеству рациональных чисел Q. То есть, множеству всех несократимых дробей вида m/n, где m — целое число, а n — натуральное.
Счётность множества всех рациональных чисел Q.
С рациональными числами вопрос похитрее будет. Тут есть одна проблемка. Проблемка состоит в том, что между любыми двумя соседними целыми числами находится бесконечно много рациональных чисел. Например, между 0 и 1 находятся дроби 1/2, 1/3, 1/4, 1/5, … И интуиция нам снова вполне справедливо подсказывает, что рациональных чисел больше, чем целых (а значит, и натуральных). Однако, как показал наш гениальный Кантор ещё в 1874 году, рациональных чисел тоже столько же, сколько и натуральных! Да-да, как это ни странно!
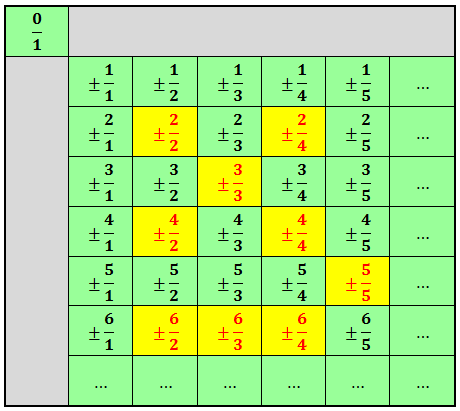
Как же тогда нам перенумеровать все-все рациональные числа? Понятное дело, что в связи с вышеописанной проблемкой выстроить все рациональные числа в один ряд уже несколько затруднительно, да… Мы поступим по-другому. 🙂 Как? Очень нетривиально! Мы составим волшебную табличку. Бесконечную в длину и в высоту…
В верхнем левом углу притаилось рациональное число 0/1. Или просто ноль. Он стоит отдельно чисто для нашего удобства, не более того.
Что будем делать дальше? А вот дальше мы будем заполнять нашу табличку рациональными числами по такому простому принципу: в первый столбец пойдут все дроби со знаменателем 1 (т.е. не что иное, как все целые числа), во второй столбец — все дроби со знаменателем 2, в третий — со знаменателем 3. И так далее… Таким образом, наша табличка станет неограниченно простирающейся вниз и вправо: числители вписываемых дробей будут меняться по вертикали, а знаменатели — по горизонтали. Кроме того, опять же для удобства и компактности, в каждую ячейку я буду вписывать сразу по два рациональных числа. С плюсом и с минусом. Всё просто.)
Кстати, вы обратили внимание, что некоторые ячейки я покрасил в другой цвет (жёлтый), а находящиеся в них дроби выделил красным шрифтом? Не догадались, зачем? Да! В жёлтых ячейках находятся сократимые дроби. Эти дроби нас не интересуют и в нашей нумерации участвовать никак не будут.
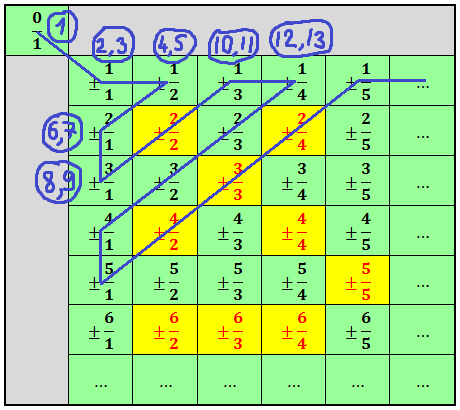
Что делаем дальше? А дальше нумеруем наши выписанные числа вот такой интересной змейкой:
Итак, всё доказано! Множество Q — счётно. 🙂 А этот факт и означает, что рациональных чисел столько же, сколько и натуральных! Миф №2 развеян.)
Заметьте снова, что нам здесь совершенно не важно, КАК мы установили наше правило нумерации! Важен только сам факт установления этого правила! Здесь мы составили табличку, запустили на неё змейку-«счётчика» и всё пронумеровали, ничего не забыв. А могли бы, например, придумать способ выстроить все рациональные числа в ряд и начать нумерацию членов ряда. И, кстати, такой способ тоже есть! Но он менее наглядный. Способов может быть много. Но факт — налицо. Все рациональные числа пронумерованы.)
А теперь предлагаю немного поразмышлять самостоятельно.
Доказать счётность множества всех точек координатной плоскости с целыми координатами.
Так, ну хорошо. Множества целых и рациональных чисел — счётны. А что же насчёт множества действительных чисел R? А вот оно уже несчётно. Увы… То есть, перенумеровать все действительные числа у нас уже не получится. Принципиально не получится. Их, действительных чисел, настолько много, что натуральных чисел (а нумеруем мы, заметьте, только такими!) нам просто не хватит. Более того, несчётно даже множество всех десятичных дробей из отрезка [0; 1]! И скоро мы это докажем. Тоже весьма красиво, между прочим. И разберёмся с тем, что же всё-таки такое мощность множества. В следующем уроке.)