Докажите что множество чисел вида 1 n счетно

Математический портал

Nav view search

Navigation

Search

Счетность и несчетность множеств. Равномощность множеств.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Примеры.

Доказать, что следующие множества счетны:

Решение.

Что и требовалось доказать.

Решение.

Что и требовалось доказать.

Решение.

Что и требовалось доказать.

Решение.

Что и требовалось доказать.

Примеры:

Доказательство.

Что и требовалось доказать.

Доказательство.

Проведем доказательство в несколько этапов:

Что и требовалось доказать.

Домашнее задание.

Доказать, что следующие множества счетны:

1.70. Используя результат задачи 1.68, доказать, что множество всех точек плскости с рациональными координатами счетно.

Источник

Разнообразие бесконечностей

Бесконечные множества содержат неограниченную последовательность элементов, объединенных общим признаком. Самые часто используемые из них в математике:

Все они бесконечны, вовсе не означает, что они равномощны.

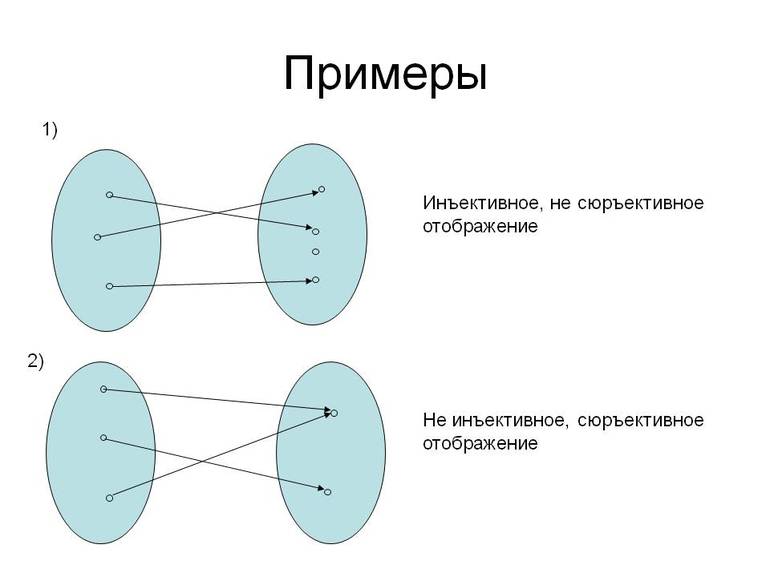
Сравнение и отображение

Числа в математике можно сравнивать друг с другом и выяснять, какое из них больше. С множествами можно производить аналогичные действия. Это будет называться их отображение друг в друга. Оно может быть дизъюнктивно, конъюнктивно и биективно. Это аналог числовых понятий «больше», «меньше» и «равно». Для того чтобы разобраться, как происходит это сравнение, нужно понятие подмножества.

Подмножеством некоторого набора компонентов называется любая часть компонентов этого набора. То есть, совокупность состоящее из чисел 1 и 3 является подмножеством множества чисел 1, 3 и 5. А они оба, в свою очередь, являются подмножествами совокупности нечётных чисел и т. д.

Если каждому компоненту множества A можно сопоставить какой-то элемент подмножества совокупности В, то отображение А в В конъюнктивно или А меньше, чем В. Если при этом нельзя найти в наборе А подмножество, которое можно сопоставить с совокупностью В, то отображение В в А дизъюнктивно. Если же каждому компоненту из комплекса А можно сопоставить элемент из совокупности В и каждому компоненту из набора В можно сопоставить элемент из совокупности А, то эти множества отображаются друг в друге биективно. В таком случае говорят, что они эквивалентны.

Для сравнения совокупностей можно использовать их мощность. Если мощность А меньше мощности В, то и множество А меньше, чем В. Если мощности равны, то сами наборы элементов эквивалентны.

Сопоставление наборов элементов

Казалось бы, используя свойства сравнения наборов элементов, можно найти соотношение мощностей бесконечных совокупностей. Ведь очевидно, что множество N является подмножеством совокупности Z, они оба являются подмножеством Q, а множества Q и I вместе составляют R. И отсюда, по определению, следует, что мощности соотносятся так: |N| |I|, и загадкой остается только соотношение совокупностей Q и I. Но всё не так просто.

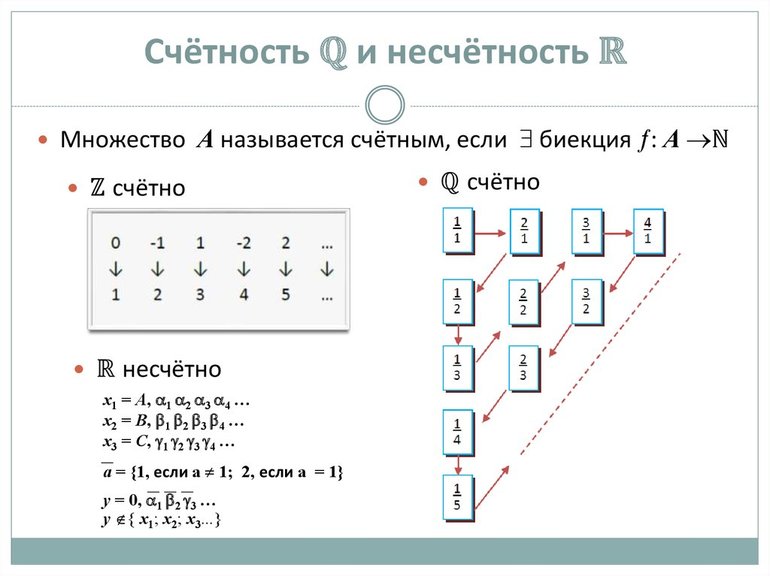
Выяснение размера бесконечного комплекса компонентов — такая же задача, как определение размера конечной совокупности — пересчёт компонентов. Возможность посчитать и пронумеровать элементы бесконечной совокупности называется счётностью. Совокупность натуральных чисел — счётная. Элементам в этом случае легко присвоить порядковые номера. И все множества, которые эквивалентны N, тоже будут счётными. Его размер |N| = a.

Но если взять R, то его элементы пронумеровать не получится. Ведь между любыми двумя точками, а прямой всегда можно поставить ещё одну. То есть, совокупность R «бесконечна вглубь»: каждый промежуток между бесконечным количеством точек содержит в себе бесконечное количество точек. Значит, свойство R — несчётность. Такие «бесконечные вглубь» множества называют континуальными. И их мощность обозначается как |R| = c.

Ещё одно важное свойство бесконечных множеств заключается в том, что если из бесконечной совокупности удалить (или добавить к ней) подмножество меньшей мощности, то размер исходной совокупности сохранится. Если из N убрать все числа от 1 до 10, то его мощность не уменьшится на 10, а останется прежней. Множество останется бесконечным и счётным: a — 10 = a.

Бесконечная мощность счётных и несчётных множеств может быть описана тремя формулами. Это два равенства и одно неравенство:

Совокупность всех точек интервала или отрезка на прямой тоже будет континуальна, так как на неё можно спроецировать всю совокупность точек действительной прямой R.

Соотношение мощностей

Континуальное множество больше счётного. Но какова их разница? Чтобы это вычислить, потребуется понятие булеан.

Что такое булеан

Есть некий набор компонентов V. Булеаном V будет называться комплекс всех его подмножеств. Как будут соотноситься размер булеана и самого V? Если V состоит из одного элемента, то его булеан будет состоять из двух элементов: пустого набора компонентов и самого V. Если V состоит из двух элементов, то булеан содержит 4 элемента: пустое множество, V и каждый из двух элементов. Если V содержит 3 элемента, то булеан содержит 8: пустое, само V, каждый из трёх его элементов в отдельности и каждую пару элементов (которых тоже три).

То есть мощность булеана — это 2 в степени размера самого V. Булеан так и записывается 2^|V|. Размер булеана всегда будет больше, чем мощность самой совокупности.

Результат сопоставления

Размер булеана любой счётной совокупности будет 2^a. Если рассматривать N, то его булеан будет состоять из пустоты, бесконечного числа элементов N, бесконечного числа пар элементов, бессчётного числа сочетаний элементов по 3, 4, 5 и так до бесконечности. Какому известному множеству можно сопоставить этот булеан?

Так как это N — натуральные числа, то каждый элемент булеана — это последовательность чисел. Если представить каждую такую последовательность в виде знаков после запятой в десятичной дроби, то получатся координаты точек в интервале от 0 до 1, который эквивалентен R. Так как булеан N содержит бесконечное количество комбинации бесконечных десятичных дробей, то он покрывает все точки в этом интервале. Это нестрогое доказательство уравнения c = 2^a.

Обозначения мощностей а и c происходят от слов account и continum, но именно такая последовательность букв порождает вопрос: а есть ли бесконечное множество мощностью b, которое меньше c, но больше a. Если и есть, то пока они неизвестны. А вот комплекс больший по мощности, чем c, есть. Это булеан континуального множества с мощностью 2^c. А у этого булеана тоже есть булеан с ещё большей мощностью.

Бесконечные множества бывают счётными и несчётными. Счётными называют те, элементы в которых можно пересчитать, то есть эквивалентные совокупности натуральных чисел. К ним относятся само множество натуральных, а также целых и рациональных чисел. Среди несчётных выделяют континуальные множества, эквивалентные совокупности всех точек на прямой. К ним относятся действительные и иррациональные числа. Континуальность является булеаном счётного набора.

Источник

Теория функций действительного переменного/Счётные множества

Доказательство проиллюстрируем следующим рисунком (в отличие от русской матем.символики здесь «/» обозначает не дробь, а стоит вместо запятой, обозначая упорядоченную пару-элемент N*N):

В результате расстановки, указанной стрелками, все элементы приобретут номер, и, значит, это множество- счётное.

Теорема 2: Декартово произведение конечного числа счетных множеств есть множество счетное.

Теорема 3: Всякое бесконечное множество содержит счетное подмножество.

Теорема 4: Всякое бесконечное подмножество счётного множества счётно.

Пусть множество A счётно, а B— его бесконечное подмножество. По предыдущей теореме множество B содержит счётное подмножество C. Так как множества A и C оба счётны, то они эквивалентны:A

A, то есть множество B эквивалентно счётному множеству и потому само счётно.

Теорему 4 можно перефразировать следующим образом: 4′ : Всякое подмножество счётного множества конечно или счётно.

Теорема 5: При любом отображении образ счётного множества конечен или счётен.

Теорема 7: Всякое семейство < Δ x >x ∈ X <\displaystyle \<\Delta _\>_> попарно не пресекающихся непустых интервалов конечно или счётно.

Теорема 8: Объединение конечной или счётной совокупности конечных или счётных множеств конечно или счётно.

Занумеруем элементы множества A_n в последовательность

причём, если A_n конечно и содержит k_n элементов, то будем считать, что первые k_n членов этой последовательности попарно различны и исчерпывают всё множество A_n, а для m>k_n, полагаем a_nm=a_nkn.

Примеры представления в форме последовательности некоторых объединений:

Теорема 9: Множество всех алгебраических чисел счетно

Замечание: Из теоремы 10 следует, что всякое бесконечное множество содержит эквивалентное ему собственное подмножество, конечное же множество таким свойством не обладает. Поэтому свойство множества иметь эквивалентную ему правильную часть можно принять за определение бесконечного множества.

Источник

Множество всех действительных чисел не счетно. Г. Кантор

И тем не менее несчетные множества суще­ствуют. Оказывается, множество всех дейст­вительных чисел — не счетно. Этот заме­чательный факт, как и теорема о счетности множества всех рациональных чисел, впервые в 1874 г. был доказан знаменитым немецким математиком Г. Кантором, основателем современной теории множеств.

Воспроизводим доказательст­во Кантора. Доказываем, что несчетным являет­ся уже множество всех действительных чисел интервала 1 (0; 1).

Каждое такое действительное число может быть записано в виде бесконечной десятичной дроби с целой частью нуль. При этом каждому действительному числу соответствует лишь од­на такая запись, за исключением действительных чисел, выражаемых конечными десятичны­ми дробями: каждое такое число, например 0,2476622021711, может быть записано двумя способами в виде бесконечной десятичной дроби:

Одна из этих записей начиная с некоторого момента содержит одни лишь нули, а другая— одни девятки. Если мы согласимся не употреблять записей, в которых, начиная с какого-нибудь места, идут одни девятки, то каждое действительное число будет иметь лишь един­ственную запись в виде бесконечной десятич­ной дроби. Докажем теперь теорему о несчет­ности множества действительных чисел от про­тивного: предположим, что множество дей­ствительных чисел [мы говорим все время о чис­лах X интервала (0 ; 1)] счетно, т.е. может быть занумеровано посредством натуральных чисел. Тогда вся совокупность действительных чисел интервала (0 ; 1) может быть записана в виде последовательности: х₁, х₂. Запишем разложение числа x_n в бесконечную десятичную дробь в виде:

суть последовательные десятичные знаки числа x_n, причем, согласно заключенному нами условию, не может слу­читься, что все десятичные знаки начиная с некоторого суть девятки. Итак, все действительные числа х [интерва­ла (0; 1)] предполагаются записанными в виде:
Табл: I

Приведем наше предположение к противоре­чию, найдя действительное число с, заклю­ченное между 0 и 1 и заведомо не входящее в табл. I. Для этого рассмотрим цифры, стоя­щие по диагонали в табл. I, а именно:

и выберем для каждого n натуральное число b_n, не превосходящее число 8 и отличное от числа a ( n) _n (например, при а ( n) _n (n) _n=8 полагаем b_n=7). Рассмотрим бесконечную десятичную дробь

то на n-м месте в разложении числа с мы должны были бы иметь цифру

тогда как действительно имеем

1 Под интервалом (а; b) числовой прямой понимает­ся множество всех действительных чисел х, удовлет­воряющих неравенству а

Источник

Докажите что множество чисел вида 1 n счетно

2. Счетность множества рациональных чисел и несчетность континуума

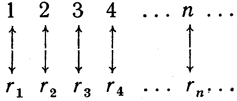
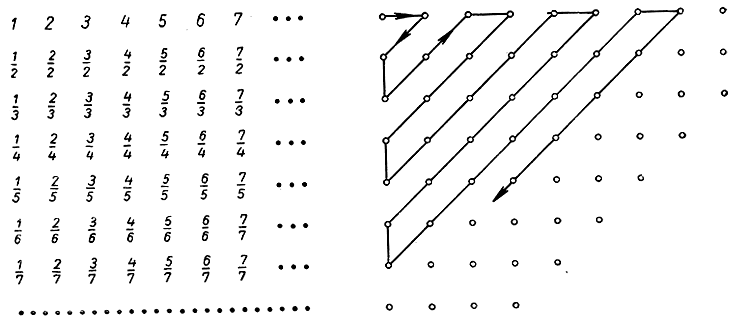
Одно из первых открытий Кантора в области анализа бесконечного заключалось в том, что множество рациональных чисел (содержащее в качестве правильного подмножества бесконечное множество натуральных чисел и потому само бесконечное) эквивалентно множеству натуральных чисел. На первый взгляд кажется странным, что всюду плотное множество рациональных чисел не более богато элементами, чем множество натуральных чисел, элементы которого «рассеяны» редко и стоят на значительном расстоянии один от другого. И в самом деле, с сохранением порядка возрастания нельзя расположить положительные рациональные числа так, как это можно сделать с натуральными: самое маленькое число а будет первым, следующее за ним по величине b вторым и т. д.; дело в том, что рациональные числа расположены всюду плотно, и потому ни для одного из них нельзя указать «следующего по величине». Но Кантор заметил, что если отказаться от требования «располагать по величине», то тогда оказывается возможным расставить все рациональные числа в ряд r₁, r₂, r₃, r₄. подобный ряду натуральных чисел. Такое расположение предметов некоторого множества в виде последовательности часто называют пересчетом («нумерацией») этого множества. Множества, для которых пересчет может быть выполнен, называются счетными или исчислимыми. Указывая один из способов пересчета множества рациональных чисел и устанавливая, таким образом, его счетность, Кантор тем самым показал, что это множество эквивалентно множеству натуральных чисел, так как

схема создает взаимно однозначное соответствие между двумя множествами. Мы опишем сейчас один из возможных способов пересчета множества рациональных чисел.

Рис. 19. Пересчет рациональных чисел

Если мы выбросим теперь все дроби, у которых числитель и знаменатель имеют отличные от 1 общие делители, то останется последовательность, в которой каждое рациональное число встретится в точности один раз:

Так устанавливается, что множество всех рациональных чисел является счетным. Принимая во внимание, что рациональные числа взаимно однозначно связаны с рациональными точками числовой прямой, можно также сказать, что множество рациональных точек на числовой прямой счетно.

Упражнения. 1) Покажите, что множество всех целых, положительных и отрицательных чисел счетно. Покажите, что множество всех рациональных, положительных и отрицательных чисел счетно.

2) Покажите, что если S и Т- счетные множества, то множество S + Т (см. стр. 138) также счетно. То же покажите для суммы трех, четырех и, вообще, n множеств; покажите, наконец, что множество, составленное посредством сложения счетного множества счетных множеств, также счетно.

Однако проведем это рассуждение фактически. Допустим, что все действительные числа, представленные в виде бесконечных десятичных дробей, расположены в виде последовательности, или списка:

где буквы N_i обозначают целую часть, а буквы а, b, с. представляют собой десятичные знаки, стоящие вправо от запятой. Мы допускаем, что эта последовательность дробей охватывает все действительные числа. Существенной частью доказательства является построение с помощью «диагональной процедуры» такого нового числа, относительно которого можно показать, что оно не входит в наш список.

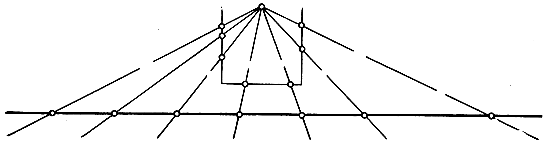
Рис. 20. Взаимно однозначное соответствие между точками согнутого интервала и точками прямой линии

Это новое число z наверняка не входит в наш список; действительно, оно не равно первому числу, стоящему в списке, так как от него отличается первой цифрой после запятой, оно не равно второму числу, так как от него отличается второй цифрой после запятой, и вообще отлично от n-го числа по списку, так как отличается от него n-й цифрой после запятой. Итак, в нашем списке, составленном будто бы из всех действительных чисел, нет числа z. Значит, множество всех действительных чисел несчетно.

Читателю может прийти в голову мысль, что несчетность континуума обусловливается неограниченной протяженностью прямой линии и что конечный отрезок прямой будет содержать лишь счетное множество точек. Чтобы убедиться в ложности такого предположения, достаточно установить, что весь числовой континуум в целом эквивалентен некоторому конечному интервалу, скажем, единичному интервалу от 0 до 1. Получить необходимое для этой цели взаимно однозначное соответствие можно, например, сгибая интервал в точках и и затем проектируя так, как показано на рис. 20. Отсюда видно, что даже конечный интервал (и, конечно, отрезок) содержит несчетное множество точек.

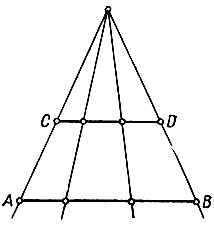
Упражнение. Показать, что любой отрезок [А, В] числовой прямой эквивалентен любому другому отрезку [С, D] (рис. 21).

Рис. 21. Взаимно однозначное соответствие между точками двух отрезков различной длины

Стоит привести еще другое доказательство несчетности континуума, носящее, пожалуй, более интуитивный характер. Достаточно (принимая во внимание последнее доказанное предложение) сосредоточить внимание на точках единичного отрезка от 0 до 1. Доказательство, впрочем, как и раньше, будет «косвенное». Предположим, что множество всех точек названного отрезка может быть расположено в виде последовательности

Источник