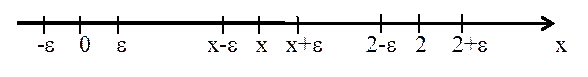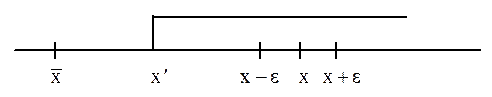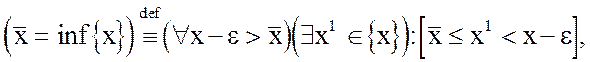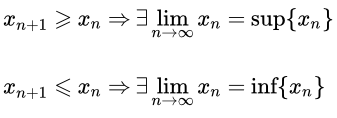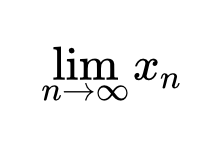Докажите что монотонная неограниченная последовательность не имеет предельной точки

Предельные точки последовательности

Лемма 1.Если x- предельная точка последовательности k>, то из этой последовательности можно выделить подпоследовательность n_k>, сходящуюся к числу x.

Из леммы 1 следует, что можно дать другое определение предельной точки последовательности, эквивалентное определению 1.

Определение 2. Точка x бесконечно прямой называется предельной точкой последовательности k>, если из этой последовательности можно выделить подпоследовательность, сходящуюся к x.

Лемма 2.Каждая сходящаяся последовательность имеет только одну предельную точку, совпадающую с пределом этой последовательности.

Замечание.Если последовательность сходится, то она в силу леммы 2 имеет только одну предельную точку. Однако, если n> не является сходящейся, то она может иметь несколько предельных точек (и, вообще бесконечно много предельных точек). Покажем, например, что <1+(-1) n >имеет две предельные точки.

Теорема.У всякой ограниченной последовательности существует хотя бы одна предельная точка.

Пусть x- любое число, превосходящее 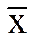. Выберем e>0 настолько малым,

что x-e>.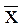

и x 1 Î, правее x 1 лежит конечное число элементов последовательности n> или их вовсе нет, т.е. x не является предельной точкой последовательности n>.

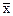
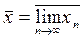
Определение.Наибольшая предельная точка последовательности n> называется верхним пределом последовательности и обозначается символом . Из замечания следует, что у всякой ограниченной последовательности есть верхний предел.

Аналогично вводится понятие нижнего предела 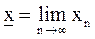(как наименьшей предельной точки последовательности n>).

Итак, мы доказали следующее утверждение. У всякой ограниченной последовательности существует верхний и нижний пределы.

Сформулируем без доказательства следующую теорему.

Теорема.Для того, чтобы последовательность 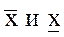n> была сходящейся, необходимо и достаточно, чтобы она была ограниченной и чтобы ее верхний и нижний пределы совпадали.

Результаты этого пункта приводят к следующей основной теореме Больцано-Вейерштрасса.

Теорема Больцано-Вейерштрасса.Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Доказательство. Так как последовательность n> ограничена, то она имеет хотя бы одну предельную точку x. Тогда из этой последовательности можно выделить подпоследовательность, сходящуюся к точке x (следует из определения 2 предельной точки).

Замечание.Из любой ограниченной последовательности можно выделить монотонную сходящуюся последовательность.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Математический анализ
Записки лекций

Илья Щуров (НИУ ВШЭ)

9 Подпоследовательности, предельные точки и теорема Больцано — Вейерштрасса

9.1 Подпоследовательности и предельные точки

9.1.1 Подпоследовательности

Доказательство первых двух пунктов этого утверждения простое и я советую его провести самостоятельно. Третий пункт вынесен в качестве задачи на семинары. Обратное неверно: если подпоследовательность обладает каким-нибудь из этих свойств (скажем, ограничена), это ничего не говорит про аналогичное свойство исходной последовательности (приведите примеры).

Неверный ответ. Попробуйте доказать 🙂

9.1.2 Предельные точки

При решении некоторых задач удобным оказывается другое определение предельной точки.

Сравните это определение с определением предела — в чём ключевое различие?

Есть ли последовательности, не имеющие предельных точек? Тут легко привести пример — скажем, последовательность a n = n обладает таким свойством: она посещает каждое натуральное число ровно один раз, а потом уходит от него на расстояние как минимум 1.

Заметим, что последовательсноть a n = n неограничена. Бывают ли ограниченные последовательности без предельных точек? Прежде, чем читать дальше, попробуйте придумать такую.

9.2 Теорема Больцано — Вейерштрасса

Для доказательства этой теоремы нам понадобится вспомогательная лемма, которая представляет и самостоятельный интерес — она пригодится нам ещё несколько раз.

9.2.1 Лемма о вложенных отрезках

Потребуем также, чтобы длины отрезков стремились к нулю:

Неверный ответ. Какие же это?

9.2.2 Деление отрезка пополам

Источник

Теорема Вейерштрасса о пределе монотонной последовательности

Теорема Вейерштрасса о пределе монотонной последовательности

Любая монотонная ограниченная последовательность < x_n > имеет конечный предел, равный точной верней границе, sup < x_n > для неубывающей и точной нижней границе, inf < x_n > для невозрастающей последовательности.
Любая монотонная неограниченная последовательность имеет бесконечный предел, равный плюс бесконечности, для неубывающей и минус бесконечности, для невозрастающей последовательности.

Доказательство

1) Пусть последовательность является неубывающей ограниченной последовательностью.

Поскольку последовательность ограничена, то она имеет конечную точную верхнюю границу
.
Это означает, что:

Поскольку последовательность ограничена, то она имеет конечную точную нижнюю границу
.
Это означает следующее:

Теперь рассмотрим неограниченные последовательности.
3) Пусть последовательность является неограниченной неубывающей последовательностью.

Поскольку последовательность неубывающая, то при имеем:
.
Здесь мы также использовали (3.2).

4) Наконец рассмотрим случай, когда является неограниченной невозрастающей последовательностью.

Поскольку последовательность невозрастающая, то при имеем:
.

Пример решения задачи

Представим последовательность в виде рекуррентных формул:
,
.

Поскольку последовательность возрастает и ограничена сверху, то она является ограниченной последовательностью. Поэтому, по теореме Вейерштрасса, она имеет предел.

Источник

Предел монотонной последовательности

Монотонная последовательность. Точные грани последовательности.

Последовательность \(\\>\) называют возрастающей (неубывающей), если для любого \(n\in\mathbb\) выполняется неравенство
$$
x_\geq x_.\label
$$
Аналогично последовательность\(\\>\) называют убывающей (невозрастающей), если для любого \(n\in\mathbb\) справедливо неравенство
$$
x_\leq x_.\label
$$
Если неравенство \eqref можно записать в виде \(x_>x_\), а неравенство \eqref — в виде \(x_ 0 \ \exists x_<\varepsilon>\in X:x_<\varepsilon>>M-\varepsilon\>.\label
$$
Аналогично определение точной нижней грани \(\displaystyle \inf\) числового множества \(X\) можно записать в виде
$$
\displaystyle \\Leftrightarrow\<\forall x\in X\rightarrow x\geq m\>\wedge\<\forall\varepsilon>0\ \exists x_<\varepsilon>\in X:x_ <\varepsilon>0\ \exists N_<\varepsilon>:x_>>a-\varepsilon\>,\label
$$
$$
[b=\displaystyle \inf\\>]\Leftrightarrow\<\forall n\in N\rightarrow x_\geq b\>\wedge\<\forall\varepsilon 0\) (рис. 6.1) найдется член последовательности, больший \(a-\varepsilon\), то есть
$$
\forall\varepsilon>0 \ \exists N_<\varepsilon>:x_>>a-\varepsilon.\label
$$

Рис. 6.1

Аналогично разъясняется определение \eqref точной нижней грани последовательности.

Признак сходимости монотонной последовательности.

Если последовательность \(\<>\>\) является возрастающей и ограниченной сверху, то существует
$$
\lim_x_=\sup\\>.\nonumber
$$

Если последовательность \(\\>\) является убывающей и ограниченной снизу, то существует
$$
\lim_x_=\inf\\>.\nonumber
$$

\(\circ\) Ограничимся доказательством теоремы для случая ограниченной сверху и возрастающей последовательности.

Если последовательность \(\\>\) ограничена сверху, то есть множество чисел \(x_<2>,x_<2>, \ldots,x_, \ldots\) ограничено сверху, то по теореме о существовании верхней грани существует точная верхняя грань этой последовательности, определяемая условиями \eqref, \eqref. Так как \(\\>\) — возрастающая последовательность, то
$$
\forall n\geq N_<\varepsilon>\rightarrow x_>\leq x_.\label
$$

Из \eqref-\eqref следует, что
$$
\forall\varepsilon>0 \ \exists N_<\varepsilon>:\forall n\geq N_<\varepsilon>\rightarrow a-\varepsilon Замечание 1.

Теорема 1 остается справедливой для последовательности, ограниченной сверху (снизу) и возрастающей (убывающей), начиная с некоторого номера.

Источник

Предел последовательности – основные теоремы и свойства

Определение последовательности

Более подробно см. страницу Определение числовой последовательности >>>.
Далее мы будем считать, что элементами последовательности являются действительные числа.

Верхнюю грань также называют точной верхней границей, а нижнюю грань – точной нижней границей. Понятия верхней и нижней граней справедливы не только к последовательностям, но и к любым множествам действительных чисел.

Определение предела последовательности

С помощью логических символов существования и всеобщности определение предела можно записать следующим образом:
.

Свойства конечных пределов последовательностей

Основные свойства

Точка a является пределом последовательности тогда и только тогда, когда за пределами любой окрестности этой точки находится конечное число элементов последовательности или пустое множество.

Теорема единственности предела числовой последовательности. Если последовательность имеет предел, то он единственный.

Если последовательность имеет конечный предел, то она ограничена.

Если у последовательности добавить, отбросить или изменить первые m элементов, то это не повлияет на ее сходимость.

Арифметические действия с пределами

Свойства, связанные с неравенствами

Бесконечно большая и бесконечно малая последовательности

Бесконечно малая последовательность

Сумма и разность конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.

Произведение ограниченной последовательности на бесконечно малую является бесконечно малой последовательностью.

Произведение конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.

Доказательства свойств бесконечно малых последовательностей приведены на странице
Бесконечно малые последовательности – определение и свойства >>>.

Бесконечно большая последовательность

Если последовательность бесконечно большая, а последовательность ограничена, то
.

Если абсолютные значения элементов последовательности ограничены снизу положительным числом ( ), а – бесконечно малая с неравными нулю элементами, то
.

Более подробно определение бесконечно большой последовательности с примерами приводится на странице
Определение бесконечно большой последовательности >>>.
Доказательства свойств бесконечно больших последовательностей приведены на странице
Свойства бесконечно больших последовательностей >>>.

Критерии сходимости последовательностей

Монотонные последовательности

Аналогичными неравенствами определяются другие монотонные последовательности.

Строго убывающая последовательность:
.
Неубывающая последовательность:
.
Невозрастающая последовательность:
.

Отсюда следует, что строго возрастающая последовательность также является неубывающей. Строго убывающая последовательность также является невозрастающей.

Монотонная последовательность – это неубывающая или невозрастающая последовательность.

Теорема Вейерштрасса. Для того чтобы неубывающая (невозрастающая) последовательность имела конечный предел, необходимо и достаточно, чтобы она была ограниченной сверху (снизу ). Здесь M – некоторое число.

Поскольку любая неубывающая (невозрастающая) последовательность ограничена снизу (сверху), то теорему Вейерштрасса можно перефразировать следующим образом:

Монотонная неограниченная последовательность имеет бесконечный предел, равный для неубывающей и для невозрастающей последовательности.

Критерий Коши сходимости последовательности

Фундаментальная последовательность – это последовательность, удовлетворяющая условию Коши.

Критерий Коши сходимости последовательности. Для того, чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она удовлетворяла условию Коши.

Доказательство критерия сходимости Коши приведено на странице
Критерий Коши сходимости последовательности >>>.

Подпоследовательности

Доказательство теоремы Больцано – Вейерштрасса приведено на странице
Теорема Больцано – Вейерштрасса >>>.

Определения, теоремы и свойства подпоследовательностей и частичных пределов рассмотрены на странице
Подпоследовательности и частичные пределы после­довательностей>>>.

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
В.А. Зорич. Математический анализ. Часть 1. Москва, 1997.
В.А. Ильин, Э.Г. Позняк. Основы математического анализа. Часть 1. Москва, 2005.

Источник