Докажите что на 8 делится куб четного числа

Доказать, что на 8 делится : куб чётного числа?

Доказать, что на 8 делится : куб чётного числа.

Любое четное число можно представить в виде 2 * а.

Е. данное выражение всегда будет кратным 8, что и необходимо было доказать.

Какие утверждения верны для любыx чисел?

Какие утверждения верны для любыx чисел?

1] куб чётного числа делится на 8 2] разность квадратов двуx нечётныx чисел делится на 8 3] квадрат четного числа делится на 8

4] разность квадратов двуx чётныx чисел делится на 8.

Сумма трех целых чисел делится на 6 доказать что и сумма кубов этих чисел делится на 6?

Сумма трех целых чисел делится на 6 доказать что и сумма кубов этих чисел делится на 6.

+ 5в 2006 степени делится на 6.

Доказать, что число 11n(в кубе) + n делится на 6, при любом n, принадлежащему множеству натуральных чисел?

Доказать, что число 11n(в кубе) + n делится на 6, при любом n, принадлежащему множеству натуральных чисел.

Доказать что (n3(в кубе) + 5n)делится на 6?

Доказать что (n3(в кубе) + 5n)делится на 6.

Срочно?

25балов n(в кубе) + 5n Доказать что делится на 6.

Как доказать что если каждое из двух четных чисел кратно 3, то сумма их кубов делится 54?

Как доказать что если каждое из двух четных чисел кратно 3, то сумма их кубов делится 54.

Какова формула чётного числа, нечетного числа?

Какова формула чётного числа, нечетного числа?

Доказать, что число 333333² + 777777³ делится на 37?

Доказать, что число 333333² + 777777³ делится на 37.

1. 1). Допустимы все значения от минус бесконечности до плюс бесконечности кроме нуля, на ноль делитьнельзя. 2). Раз знаменатель не должен равняться нулю, то находим это значение для «а» в знаменателеи исключаем его из множества допустимых значений..

Источник

Докажите что на 8 делится куб четного числа

Задача 15:

Найдите остатки от деления

а) 1989 • 1990 • 1991 + 1992³ на 7;

Решение:

Ответ: а) 0; б) 1, так как 9 дает остаток 1 при делении на 8.

Задача 16:

Докажите, что n³ + 2n делится на 3 для любого натурального n.

Решение:

Число n может давать при делении на 3 один из трех остатков: 0, 1, 2. Рассмотрим три случая.

Если n дает остаток 0, то и n³ и 2n делятся на 3 и поэтому n³ + 2n также делится на 3.

Если n дает остаток 1, то n³ дает остаток 1, 2n – остаток 2, а 1 + 2 делится на 3.

Если n дает остаток 2, то n² дает остаток 1, n³ – остаток 2, 2n – остаток 1, а 2 + 1 делится на 3.

Задача 17:

Докажите, что n 5 + 4n делится на 5 при любом натуральном n.

Решение:

Указание: Переберите остатки от деления на 5.

Задача 18:

Докажите, что n² + 1 не делится на 3 ни при каком натуральном n.

Решение:

Переберите остатки от деления на 3.

Задача 19:

Докажите, что n³ + 2 не делится на 9 ни при каком натуральном n.

Решение:

Переберите остатки от деления на 9.

Задача 20:

Докажите, что n³ – n делится на 24 при любом нечетном n.

Решение:

Указание: Докажите, что указанное число делится и на 3, и на 8.

Задача 21:

а) Докажите, что p² – 1 делится на 24, если p – простое число и p > 3.

б) Докажите, что p² – q² делится на 24, если p и q – простые числа, большие 3.

Решение:

Указание: Докажите, что указанные числа делятся и на 3 и на 8.

Задача 22:

Натуральные числа x, y, z таковы, что x² + y² = z². Докажите, что хотя бы одно из этих чисел делится на 3.

Решение:

Если ни x, ни y не делятся на 3, то x² и y² дают остаток 1 от деления на 3. Таким образом, их сумма имеет остаток 2 от деления на 3. Но z² не может иметь такого остатка.

Задача 23:

a и b – натуральные числа, причем число a² + b² делится на 21. Докажите, что оно делится и на 441.

Решение:

Проверьте, что и a и b делятся и на 3 и на 7.

Задача 24:

a, b, c – натуральные числа, причем a + b + c делится на 6. Докажите, что a³ + b³ + c³ тоже делится на 6.

Решение:

Проверьте, что числа x³ и x имеют одинаковые остатки от деления на 6.

Задача 25:

Три простых числа p, q и r, большие 3, образуют арифметическую прогрессию: p = p, q = p + d, r = p + 2d. Докажите, что d делится на 6.

Решение:

Если d – нечетно, то среди чисел p и q есть четное, что невозможно. Если d не делится на 3, то среди чисел p, q и r есть делящееся на 3, что тоже невозможно.

Задача 26:

Докажите, что сумма квадратов трех натуральных чисел, уменьшенная на 7, не делится на 8.

Решение:

Выясните возможные остатки квадратов при делении на 8.

Задача 27:

Сумма трех натуральных чисел, являющихся точными квадратами, делится на 9. Докажите, что из них можно выбрать два, разность которых также делится на 9.

Решение:

Возможные остатки квадратов от деления на 9: 0, 1, 4, 7. Проверьте, что если сумма трех из них делится на 9, то среди них есть два одинаковых.

Задача 28:

Решение:

Так как при нахождении последней цифры очередной степени числа 9 достаточно умножить на 9 лишь последнюю цифру предыдущей степени, то ясно, что за 9 следует 1 (9 • 9 = 81), а за 1 – 9 (1 • 9 = 9).

Таким образом, нечетные степени девятки оканчиваются на 9. Поэтому последняя цифра числа 1989 1989 – девятка.

Задача 29:

Решение:

Выпишем последние цифры нескольких начальных степеней двойки: 2, 4, 8, 6, 2, …. Мы видим, что 2 5 так же, как и 2¹, оканчивается на 2. Поскольку очередная цифра полностью определяется последней цифрой предыдущей степени, то произойдет «зацикливание»: 2 6 (как и 2²) оканчивается на 4, 2 7 (как и 2³) – на 8, 2 8 – на 6, 2 9 – на 2 и т.д. Поскольку длина цикла равна 4, то последняя цифра числа 2 50 определяется остатком от деления числа 50 на 4. Так как он равен 2, то последняя цифра числа 2 50 совпадает с последней цифрой числа 2², то есть равна 4.

Задача 30:

Решение:

Задача 31:

Найдите остаток от деления 2¹ºº на 3.

Решение:

Выпишите остатки от деления на 3 нескольких начальных степеней двойки. Докажите, что здесь происходит «зацикливание».

Задача 32:

Найдите остаток от деления 3 1989 на 7.

Решение:

Задача 33:

Докажите, что 2222 5555 + 5555²²²² делится на 7.

Решение:

Вычислите остаток от деления этого числа на 7 и убедитесь, что он равен нулю.

Задача 34:

Найдите последнюю цифру числа .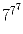

Задача 35:

а) p, p + 10, p + 14 – простые числа. Найдите p.

б) p, 2p + 1, 4p + 1 – простые числа. Найдите p.

Решение:

Рассмотрите остатки от деления на 3. Одно из этих чисел делится на 3. а) p = 3; б) p = 3.

Задача 36:

p и 8p² + 1 – простые числа. Найдите p.

Решение:

Задача 37:

p и p² + 2 – простые числа. Докажите, что p³ + 2 – также простое число.

Решение:

Задача 38:

Докажите, что не существует натуральных чисел a и b таких, что a² – 3b² = 8.

Решение:

Рассмотрите остатки по модулю 3.

Задача 39:

а) Может ли сумма квадратов двух нечетных чисел быть квадратом целого числа?

б) Может ли сумма квадратов трех нечетных чисел быть квадратом целого числа?

Решение:

Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.

Задача 40:

Докажите, что сумма квадратов пяти последовательных натуральных чисел не является точным квадратом.

Решение:

Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.

Задача 41:

p, 4p² + 1 и 6p² + 1 – простые числа. Найдите p.

Ответ: p = 5. Рассмотрите остатки при делении на 5.

Задача 42:

Докажите, что число 100 … 00500 … 001 (в каждой из двух групп по 100 нулей) не является кубом целого числа.

Решение:

Это число дает остаток 7 от деления на 9.

Задача 43:

Докажите, что a³ + b³ + 4 не является кубом целого числа ни при каких натуральных a и b.

Решение:

Выясните, какой остаток может давать число a³ + b³ + 4 от деления на 9.

Задача 44:

Докажите, что число 6n³ + 3 не является шестой степенью целого числа ни при каком натуральном n.

Решение:

Выясните, какой остаток может давать число 6n³ + 3 от деления на 7.

Задача 45:

x, y, z – натуральные числа, причем x² + y² = z². Докажите, что xy делится на 12.

Решение:

Если ни одно из чисел x, y не делится на 3, то z² дает остаток 2 при делении на 3, что невозможно. Заметьте теперь, что квадрат нечетного числа при делении на 8 дает остаток 1, квадрат четного числа, не делящегося на 4, – остаток 4, квадрат числа, делящегося на 4, – остаток 0. Докажите, что либо x и y оба четны, либо среди них есть число, кратное 4.

Источник