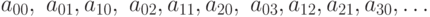Докажите что объединение двух счетных множеств является счетным множеством

06. Теоремы о счетных множествах. Множества мощности континуум

Если рассмотреть любое конечное множество и любое его собственное (непустое и не совпадающее с ним самим) подмножество, то элементов в подмножестве меньше, чем в сам множестве, т. е. часть меньше целого.

Обладают ли бесконечные множества таким свойством? И может ли иметь смысл утверждение, что в одном бесконечном множестве «меньше» элементов, чем в другом, тоже бесконечном? Ведь про два бесконечных множества мы можем пока только сказать, эквивалентны они или нет. А существуют ли вообще неэквивалентные бесконечные множества?

Приведём забавную фантастическую историю из книги Н. Я. Виленкина «Рассказы о множествах». Действие происходит в далёком будущем, когда жители разных галактик могут встречаться друг с другом. Поэтому для всех путешествующих по космосу построена огромная гостиница, протянувшаяся через несколько галактик.

В этой гостинице бесконечно много номеров (комнат), но, как и положено, все комнаты пронумерованы, и для любого Натурального числа n есть комната с этим номером.

Однажды в этой гостинице проходил съезд космозоологов, в котором участвовали представители всех галактик. Так как галактик тоже бесконечное множество, все места в гостинице оказались занятыми. Но в это время к директору гостиницы приехал его друг и попросил поселить его в эту гостиницу.

«После некоторых размышлений директор обратился к администратору и сказал:

– Куда же я дену жильца этого номера? – удивлённо спросил администратор.

– А его переселите в № 2. Жильца же из № 2 отправьте в № 3, из № 3 – в № 4 и т. д.»

Вообще, пусть постоялец, живущий в номере K, переедет в номер K+1, как это показано на следующем рисунке:

Тогда у каждого снова будет свой номер, а № 1 освободится.

Таким образом, нового гостя удалось поселить – именно потому, что номеров в гостинице бесконечно много.

Первоначально участники съезда занимали все номера гостиницы, следовательно, между множеством космозоологов и множеством N Было установлено взаимно однозначное соответствие: каждому космозоологу дали по номеру, на двери которого написано соответствующее ему натуральное число. Естественно считать, что делегатов было «столько же», сколько имеется натуральных чисел. Но приехал ещё один человек, его тоже поселили, и количество проживающих увеличилось на 1. Но их снова осталось «столько же», сколько и натуральных чисел: ведь все поместились в гостиницу!

Мы пришли к удивительному выводу: если к множеству, которое равномощно N, добавить ещё один элемент, получится множество, которое снова равномощно N. Но ведь совершенно ясно, что делегаты-космозоологи представляют собой часть того множества людей, которые разместились в гостинице после приезда нового гостя. Значит, в этом случае часть не «меньше» целого, а «равна» целому!

Итак, из определения эквивалентности (которое не приводит ни к каким странностям в случае конечных множеств) следует, что часть бесконечного множества может быть эквивалентна всему множеству.

Новый постоялец не удивился, когда на другое утро ему предложили переселиться в № 1000000. Просто в гостиницу прибыли запоздавшие космозоологи из галактики ВСК-3472, и надо было разместить ещё 999999 жильцов.

Эта задача оказалась весьма сложной. Но и в этом случае нашёлся выход.

«В первую очередь администратор приказал переселить жильца из № 1 в № 2.

– А жильца из № 2 переселите в № 4, из № 3 – в № 6, вообще, из номера N – в номер 2n.

Определение. Множество А, равномощное множеству натуральных чисел N, называется Счетным множеством (имеет мощность счетного множества). Если множество В является бесконечным и не равномощно множеству N, то его называют несчетным.

Множество, которое является конечным или счетным, еще называют не более чем счетным .

Пусть множество А является счетным. По определению, тогда существует биекция А на N, т. е. каждому аÎА соответствует единственный номер nÎN и множество А обращается в некоторую последовательность <аn>.

Теорема 1. Любое подмножество счетного множества не более чем счетно.

Доказательство. Пусть А = — счетное множество и В Í А. Если В конечное множество, то утверждение доказано. Предположим, что В бесконечное множество. Те элементы А, которые попали в В будут иметь некоторые номера в порядке возрастания: . Тогда необходимая нам биекция, показывающая, что В является счетным множеством, задается в виде: ® k.

Теорема 2. Объединение конечного или счетного числа счетных множеств является счетным множеством.

Теорема 3. Любое бесконечное множество содержит счетное подмножество.

Доказательство. Выберем в заданном множестве А какой-либо элемент, придав ему единичный индекс: а1. Среди всех оставшихся элементов множества А найдется не равный а1 элемент (в силу бесконечности А). Его мы обозначим через а2. Продолжая этот процесс до бесконечности мы получим необходимое нам счетное множество .

Доказательство. Пусть множество М – А не более чем счетно. Тогда множество М = АÈ(М – А) по теореме 2 не более чем счетно. Это противоречит тому, что множество М несчетно и, следовательно, наше исходное предположение не верно. Таким образом, множество М – А несчетно. Последнее еще не означает равномощности множеств М и М – А. Докажем ее. Выделим из М – А счетное множество В. Обозначим через С множество С = (М – А) – В. Справедливы равенства М = АÈВÈС и М – А = ВÈС. Множество АÈВ счетно (теорема 2). Следовательно, существует биекция f из АÈВ на А. Теперь можно построить биекцию g из М на М – А по правилу:

Теорема 5. Если множество С бесконечно, а В не более чем счетно, то множество ВÈС равномощно множеству С.

Доказательство. Если множество С счетно, то множество ВÈС также счетно и следовательно они равномощны. Если же множество С не счетно, то мы можем воспользоваться теоремой 4, положив в ней А = СÇВ, а М = С.

Теорема 6. Если множество С является бесконечным, то существует его подмножество В такое, что В¹С и В равномощно с С.

Доказательство. По теореме 3 мы можем выделить из множества С его счетное подмножество А. Если множество С счетно, то в качестве В из утверждения теоремы можно взять В=А. Если же С не счетно, то можно положить В=С-А и утверждаемое вытекает из теоремы 4.

Теорема 7. Множество рациональных чисел Q является счетным.

Доказательство. Обозначим через Р множество всех пар натуральных чисел (p, q), таких что p и q не имеют общих целых делителей, кроме единицы. Для пары натуральных чисел (p, q) введем ее высоту m = p + q. Обозначим Рn множество пар натуральных чисел высоты n. Нетрудно проверить, что каждое множество Рn является конечным и содержит не более, чем n-1 член. Так как Р = Èn Рn, то множество Р счетно в силу теоремы 2.

Теорема 8. Множество точек интервала (0,1) является несчетным.

Доказательство (Диагональный метод Кантора). Доказательство проведем от противного, предположив, что множество точек интервала (0,1) является счетным. Тогда все точки можно записать в виде последовательности:

Множества, равномощные множеству точек интервала (0, 1), называются множествами мощности Континуум .

Задачи.

1. Показать, что если множества А и В являются счетными, то и их произведение А´В является счетным.

2. Установить биекцию между множеством N всех натуральных чисел и множеством Q всех четных положительных чисел.

3. Установить биекцию между множеством N всех натуральных чисел и множеством Р всех четных чисел.

Источник

Счетные множества

Множество называется счетным, если оно равномощно множеству 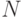натуральных чисел, то есть если его можно представить в виде (здесь — элемент, соответствующий числу ; соответствие взаимно однозначно, так что все различны).

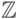
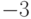
Например, множество целых чисел счетно, так как целые числа можно расположить в последовательность , , , , , , ,

(а) Подмножество счетного множества конечно или счетно.

(в) Объединение конечного или счетного числа конечных или счетных множеств конечно или счетно.

(а) Пусть — подмножество счетного множества . Выбросим из последовательности те члены, которые не принадлежат (сохраняя порядок оставшихся). Тогда оставшиеся члены образуют либо конечную последовательность (и тогда конечно), либо бесконечную (и тогда счетно).

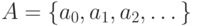
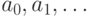
(в) Пусть имеется счетное число счетных множеств Расположив элементы каждого из них слева направо в последовательность ( ) и поместив эти последовательности друг под другом, получим таблицу

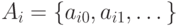
Замечание. В доказательстве утверждения (б) теоремы 2 есть тонкий момент: на каждом шаге мы должны выбрать один из оставшихся элементов множества ; такие элементы есть, но у нас нет никакого правила, позволяющего такой выбор описать. При более формальном построении теории множеств тут нужно сослаться на специальную аксиому, называемую аксиомой выбора. Законность этой аксиомы вызывала большие споры в начале 20-го века, но постепенно к ней привыкли, и эти споры сейчас почти не воспринимаются. В середине века великий логик Курт Гедель доказал, что аксиому выбора нельзя опровергнуть, пользуясь остальными аксиомами теории множеств, а в 1960-е годы американский математик Пол Дж.Коэн доказал, что ее нельзя и вывести из остальных аксиом. (Конечно, понимание этих утверждений требует подробного изложения теории множеств как аксиоматической теории.)

30. Такой же тонкий момент (хотя и менее очевидный) есть и в доказательстве утверждения (в). Можете ли вы догадаться, где он? (Ответ: мы знаем, что множества счетны, то есть что существует взаимно однозначное соответствие между и . Но нужно выбрать и фиксировать эти соответствия, прежде чем удастся построить соответствие между объединением всех и .)

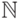
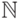
Еще несколько примеров счетных множеств:

31. Докажите, что любое семейство непересекающихся интервалов на прямой конечно или счетно. (Указание: в каждом интервале найдется рациональная точка.)

33. Докажите, что множество точек строгого локального максимума любой функции действительного аргумента конечно или счетно.

Докажите, что множество точек разрыва неубывающей функции Действительного аргумента конечно или счетно.

Источник

Счетные множества и их свойства (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3

М1. Счетные множества и их свойства. Счетность множества рациональных и алгебраических чисел. Несчетность множества действительных чисел. Существование трансцендентных чисел.

Опр1: множествово называется счетным, если оно равномощно множеству N. (2 множества называются равномощн, если одно из них можно биективно отобразить на другое).

Опр2: множество называется счетным, если все его элементыты можно занумеровать, используя по одному разу все натуральные числа.

Бесконечное множество, отличное от счетного, называется несчетным.

Пр: N, Z, множество четных чисел, множество простых чисел.

Свойства счетных множеств:

1) Всякое бесконечное подмножество счетного множества счетно.

2) Если к бесконечному множеству добавить счетное или конечное множество, то его мощность не изменится.

3) объединение конечного числа счетных множеств счетно.

4) Объединение счетного семейства счетных множеств счетно.

5) Объединение счетного семейства конечных множеств счетно или конечно.

6) Объединение счетного и конечного множеств счетно.

7) Не существует бесконечных множеств мощностью меньше чем счетное.

8) Если из бесконечного несчетного множества удалить счетное или конечное, то его мощность не изменится.

9) Если некоторое множество представить в виде прямого произведения конечного числа счетных, то оно само является счетным.

Теор: множество Q счетно.

Теор: множество R и множество N неравномощны.

Т: множество алгебраических чисел счетно.

Д: 1) Пусть P3 – множество многочленов 3-й степени с целыми коэффициентами. Пусть C4 – множество упорядоченных четверок из целых чисел, у которых первое число отлично от 0. C4 – счетно, как прямое произведение 4-х счетных множеств.

pP3 p=a3x3+a2x2+a1x+a0 (a3≠0). Многочлену p сопоставим упорядоченный набор его коэффициентов

p=a3x3+a2x2+a1x+a0 (a3≠0) → (a3, a2, a1, a0) C4. f: P3→C4 – биекция. Т. к. P3 счетно, то и C4 счетно. Аналогично доказывается счетность Pn при любом фиксированном n.

2) Пересчитаем все многочлены:

3) Рассмотрим любой многочлен, например 5-й степени, у него корней не более пяти. Каждый многочлен

имеет конечное число корней Множество А алгебраических чисел счетно или конечно как счетное семейство конечных. АN, значит А бесконечно, т. е. счетно.

Сл: существуют трансцендентные числа, их бесконечно много, их мощность больше чем чисел алгебраических.

Д: Пусть Т – множество трансцендентных чисел, R=AυT. Т не может быть Ø, конечным или счетным, т. к. R было бы счетным, а это не так. Т. о. |T|>|A|

М2. Предел числовой последовательности. Теоремы о существовании предела.

Опр1: Если каждому натуральному числу n поставлено в соответствие единственное действительное число, то говорят, что дана числовая последовательность. Обозначается y=f(n), (Xn): x1, x2,…, xn,…(*)

Опр2: числовая последовательность это функция заданная на множестве всех натуральных чисел.

Числовая последовательность (*) считается заданной, если указан закон, с помощью которого по номеру места в последовательности всегда можно назвать число, стоящее на этом месте.

Опр: число а называется пределом последовательности xn если для любого положительного числа δ (сколь угодно малого) существует такой номер N, что для всех номеров n>N выполняется неравенство: |xn—a| 1, то конечного предела не имеет.

Т: Если последовательность имеет предел, то он единственный.

Т: Если последовательность xn имеет предел, то она ограничена.

Т: тогда и только тогда, когда последовательность можно представить в виде суммы этого предела и бесконечно малой последовательности.

Т: Пусть даны 3 последовательности xn, yn, zn, такие что xn≤yn≤zn. Если , то и .

Т: (Вейерштрасса) Всякая возрастающая (неубывающая) ограниченная сверху последовательность имеет предел.

Д: т. к. xn ограничена сверху, то существует ТВГ, обозначим ее b. Тогда xn≤b b-δ

xn b-δ xN b

В силу возрастания при n>N xn>xN>b-δ, т. е. xn>b-δ (2) . Одновременно выполняются (1) и (2),b-δ 0 найдется такое число δ>0, что для всех значений xD(f) и удовлетворяющих неравенству 0 0, так чтобы если |x-6| 0, мы видим, что для всех х, удовлетворяющих неравенству |x-6| 0 в ∆, то f(x) строго возр на ∆, если f'(x) 0 то f(x2)-f(x1)≥0, f(x1)≤ f(x2). Итак из х1 0, то х+∆х>x и т. к. f(x) неубыв то f(х+∆х)≥f(x) т. е. ∆y≥0, (1)

2) ∆х 0 (f»(x) f(x0)). Эти точки наз точками локальных экстремумов.

Опр: знач-я ф-ии в т-ках лок-х экстремумов наз лок-ми экстремумами.

Т: (необх усл экстремума диф-мой ф-ии) если x0 точка лок-го экстр-ма ф-ии y=f(x) и в точке x0 существ f'(x0), то она с необх-ю =0.

Ф-я м-т иметь экстр-м и в тех точках, где производная не сущ: н-р y=|x|. D=R, f-непр, по опр х0=0 точка лок-го мин-ма, но как изв-но произв-я в этой точке не сущ.

Опр: внутр точки х, принадл-е обл-ти опр-я ф-ии, в кот f'(x)=0 или вовсе f'(x) не сущ, назыв-ся критическими точками, а те из них, в кот f'(x)=0 наз-ся в частности стационарными.

Т: (2-е дост усл экстр) пусть х0 стационарная точка ф-ции f(x) и в т х0 сущ произв-я 2-го пор-ка, тогда если f»(x0) 0, то х0 точка мин. Если f»(x0)=0, то теор ответа не дает.

Пусть х0 внутр точка обл опр-я ф-ции f(x) и в этой точке сущ f'(x), т. е. график имеет касательную.

Опр: точка М0(х0,f(x0)) наз точкой перегиба гр-ка ф-ии f(x), если в точке х0 гр-к имеет касат-ю, а слева и справа от х0 гр-к имеет разные направления выпуклости (гр-к лежит по разные стороны от кас-й к гр-ку)

Т: (необх усл т-ки перегиба) Пусть х0 точка перегиба гр-ка ф-ии f(x) и ф-ия имеет непрерывную производную 2-го пор-ка, тогда с необх-ю f»(x0)=0.

(теор справ-ва и без треб-я непр-ти 2-й произв-й, знач точки перегиба м/б лишь в тех случ-х, где f»(x0)=0 или не сущ)

Т: (дост усл т-ки перегиба) пусть f(x) в нек окр-ти точки х0 имеет f»(x) кроме м/б самой точки х0 в кот все-таки сущ произв-я 1-го пор-ка, тогда если f»(x) меняет знак при переходе через точку х0, то х0 точка перегиба.

М7. Опр и св-ва степени.

Опр: Степенью числа а с нат пок-м n наз-ся произвед n множ-лей, кажд из кот равен а:

число а наз основ-ем степени, рез-т возвед в степ аn степенью с нат пок-лем.

При а≠0 по опред а0=1, 00не определен

При а≠0 по опред а-1=1/a

Первой степ-ю числа а наз само число а1=а, вторую степ числа а: а2=а*а наз кв-том числа, третью – кубом.

Опр: рац степ-ю (mZ, nN) положит-го действ числа а наз число

Из шк курса изв-ны св-ва степ с рац пок-лем. рац чисел r и s и неотр-х чисел вы прав-ва:

1) aras=ar+s, 2) ar:as=ar-s, 3) (ar)s=ar*s,

4) (ab)r=arbr, 5) (a/b)r=ar/br,

6) пусть rQ и 00, ar>br при r s след ar>as при a>1, ar

Для того чтоб опр-ть понятие иррац степ числа, сформулируем важное св-во ирррац чисел и 2 леммы:

Т: для кажд иррац числа μ сущ возрастающая (неуб) посл-ть рац чисел r1, r2,…, rn,… сходящаяся к μ, т. е. .

Л1: Для посл-ти рац чисел r1, r2,…, rn,…, сход-ся к 0, посл-ть

(где a>0)сх-ся к 1, т. е

Л2: пусть a>0 и μ некот иррац число. Тогда для люб посл-ти рац чисел r1, r2,…, rn,…, сход-ся к μ, посл сх-ся к одному и тому же пределу А.

Д: а) если а=1 то лемма очевидна, в эт случ А=1

б) пусть a>1. Рассм сначала некот фиксир неубыв посл рац чисел

ρ1≤ ρ2≤…≤ ρn≤…, сх-ся к μ, тогда (*)

Возьмем рац число r> μ, тогда для люб n будет ρn 0, т. к. и посл-ть (*) неубыв. Возьмем теперь произв посл чисел rn сх-ся к μ, тогда посл рац чисел r1-ρ1, r2-ρ2,…, rn-ρn,… будет сх-ся к 0 и по Л1:

. Но , сл-но

в) остается рассм случай когда 01 и по док-му выше для люб посл рац чисел rn, сходящейся к μ, сущ один и тот же предел , лемма док-на.

Т. о. мы получили, что для люб посл-ти рац чисел r1, r2,…, rn,…, сход-ся к μ, послед-ть сход-ся к одному и тому же пределу А. Число принимается за значение aμ: (**) если rn→μ. Полученная ф-ла м/б док-на и в случае рац μ. В этом случае ,

но rn-μ→0, а по лемме и по теор о пределе произведения .

μ, νI справ-вы св-ва:

1) осн св-во степени: аμ+ν=аμаν

М8. Показательная ф-я, ее св-ва. Разложение в степенной ряд.

Опр: ф-я, заданная ф-лой y=ax (где a>0, a≠1, xR) наз-ся показат-й ф-ей с основанием а.

Д: для этого по следствию из 2-й теор Больцано-Коши дост установить, что sup(ax)=+∞, inf(ax)=0 (*)

Представим величину а в виде a=1+h, где h>0. По нер-ву Бернулли при имеем an=(1+h)n≥1+nh, откуда ясно, что an→+∞, при n→∞. C другой стороны a-n→0, отсюда и следуют формулы (*)

3) ф-я не является ни четной ни нечетной.

4) характ особенность: она нигде не обращается в 0, каково бы ни было число a>0 (т. е. гр-к показат ф-ции нигде не пересекает ось Ох).

5) пром-ки знакопостоянства: y>0 при всех хR.

6) пр-ки монотонности: при 0R, при a>1 ф-я возрастает при всех хR.

7) непрер на всей обл опред.

8)диф-ма на всей числ прямой, (ax)’=axlna, причем если a=e, то (ex)’= ex.

9) разложение ф-ии в ряд Тейлора м/б получено: y=ax=exlna. Пусть xlna=t, тогда на обл сходимости тогда

или

10) график функции:

Т. к. ф-я y=ax строго монотонна и непрерывна, то для нее сущ обратная: y=logax – логарифмическая, при этом x>0, E(y)=R, непрерывная и строго монотонная на (0;+∞

М9. Логарифмическая ф-я, ее осн св-ва. Разложение в степенной ряд.

Опр: ф-я, заданная ф-лой y=logax, где a>0, a≠1, наз-ся логарифм-й ф-ей. Осн. св-ва:

3) Лог ф-я по опр явл обратной по отношению к показательной ф-ии y=ax (где a>0, a≠1, xR), поэтому ее гр-к легко представить по гр-ку показ ф-ии

-ф-я не явл ни четной ни нечетной,

-нули ф-ии y=0 при х=1,

-пр-ки знакопостоянства: при 00 при х(0;1), y 1 y>0 при х(1;+∞), y 0, a≠1) диф-ма на D(f) причем

Д: дадим х приращение Δх≠0, так чтобы (х+Δх)D(y) и найдем

ч. т.д.

Т. к. люб логарифм всегда м-но свести к натур-му по ф-ле перехода от одного основ к др-му, то:

6) Обычно рассм-ся для разложения в ряд Тейлора в окр-ти х0=0 ф-я y=loga(1+x) ч)поэтому рассм-ся ф-я y=ln(1+x)

этот ряд сх-ся медленно и практически неудобен для вычисления логарифмов.

М10. Тригонометрические ф-ии, их основные св-ва. Разложение синуса и косинуса в степенной ряд.

Рассм прямоуг дек сист корд ХОУ и единичную окружность с центром в т. (0;0). Рассм в-р . Повернем в-р на ч радиан (xR). Получим вектор . Пусть В(αx;βx).

Опр:

Т. к. точка В лежит на единичной окр-ти с ц-ром (0;0), то верно след: sin2x+cos2x=1 xR.

Источник