Докажите что около любого тетраэдра можно описать сферу
638. Докажите, что: а) около любого тетраэдра можно описать сферу; б) в любой тетраэдр можно вписать сферу.
а) Докажем, что через любые 4 точки, не лежащие в одной плоскости, можно провести сферу и притом только одну. (см.ниже).
Геометрическим местом точек пространства, равноудаленных от концов отрезка, является плоскость, перпендикулярная этому отрезку и проведенная через его середину. Следовательно, центр сферы, описанной около тетраэдра, принадлежит каждой из плоскостей, проведенных через середины ребрер тетраэдра перпендикулярно к этим ребрам.
Пусть О — центр окружности, описанной около грани АВС тетраэдра, d— прямая, которая проходит через точку О, d ⊥ плоскости АВС. Все точки прямой d равноудалены от точек А, В и С. (ОА=ОВ=ОС=r — радиус описанной окружности). Если точка S ∈ d, то прямоугольные треугольники SOA, SOB, SOC равны двум катетам. Следовательно, SA=SB=SC.
Пусть плоскость α проходит через середину ребра DA и плоскость α ⊥ DA. Докажем, что d и α пересекаются. Предположим, что α || d.
Если α ⊥ AD и d ||α, то AD ⊥ d. Кроме того, d ⊥ АВ (поскольку d ⊥ плоскости АВС), и, значит d ⊥ ABD — по признаку перпендикулярности прямой плоскости.
Таким образом, через точку А проведены две различные плоскости АВС и АВD, перпендикулярные к одной прямой, что невозможно. Значит предположение, что d || α неверно.
Значит, пусть точка S точка пересечения d и α. Тогда SD=SA, т.к. S принадлежит каждой плоскости, проходящей через середину ребра тетраэдра и перпендикуляра к этому ребру.
Пусть точка О равноудаленна от всех вершин тетраэдра.
Расстояние от точки О до одной из вершин тетраэдра обозначим R. Сфера с центром О и радиусом R проходит через все данные точки. Из этого доказательства следует, что такая сфера может быть только одна.
Что и требовалось доказать. б) Рассмотрим двугранный угол. Геометрическое место точек, равноудаленных от обеих граней двугранного угла, это плоскость, которая делит двугранный угол пополам. Значит центр сферы, вписанной в тетраэдр, равноудален от всех граней пирамиды, и он должен принадлежать каждой из биссекторных плоскостей, то есть это точка пересечения биссекторных плоскостей всех двугранных углов тетраэдра. Т.к. все точки биссекторной плоскости лежат между гранями двугранного угла, то центр сферы, вписанной в тетраэдр, всегда находится внутри тетраэдра.
Центр у вписанной сферы может быть только один. Сфера с радиусом, равным расстоянию от этой точки до плоскости какой-либо грани тетраэдра, касается всех граней тетраэдра. Следовательно, в любой тетраэдр можно вписать сферу и притом только одну.
Теперь докажем 2 факта, которые использовались в доказательстве.
1) В любой трехгранный угол можно вписать сферу.
2) Биссекторные плоскости двугранных углов тетраэдра пересекаются в одной точке.
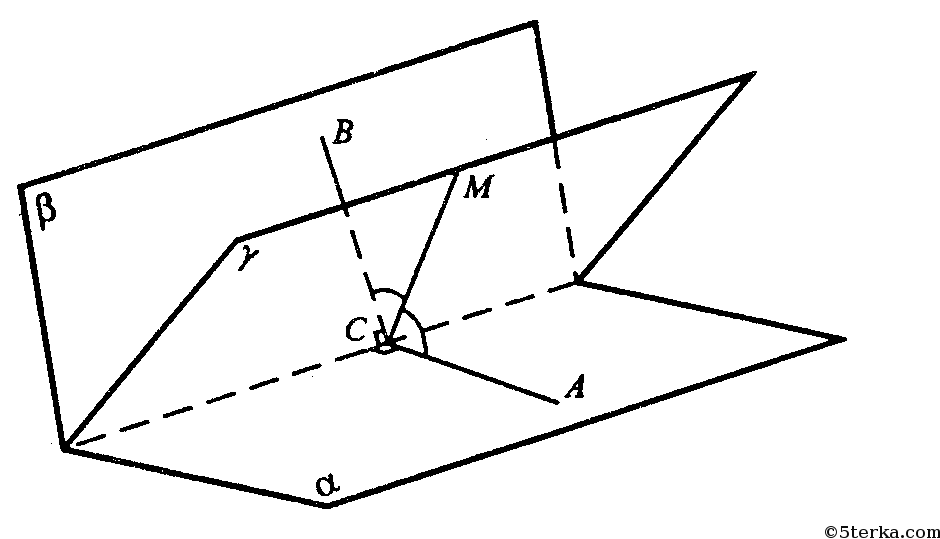
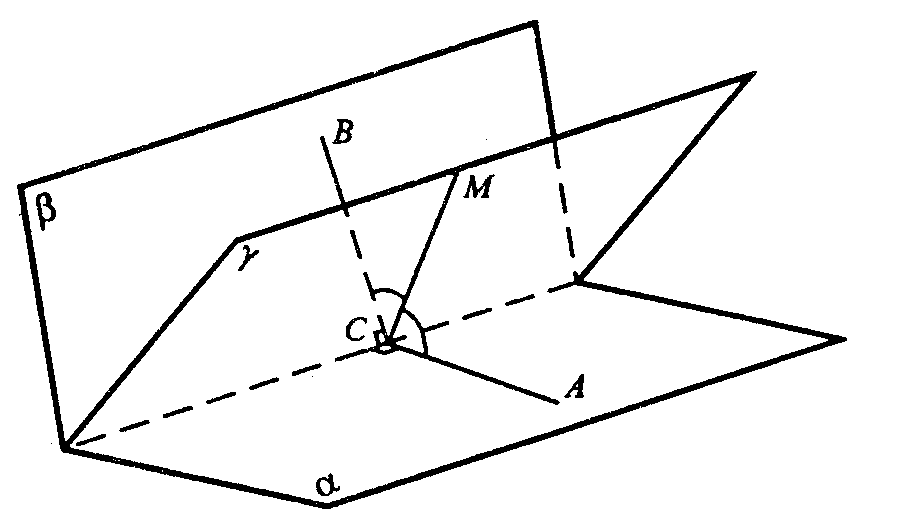
∠AСB — линейный угол двугранного угла между плоскостями α и β.
Пусть γ делит этот двугранный угол так, что ∠BСМ=∠АСМ. Таким образом, γ биссекторная плоскость данного двугранного угла.
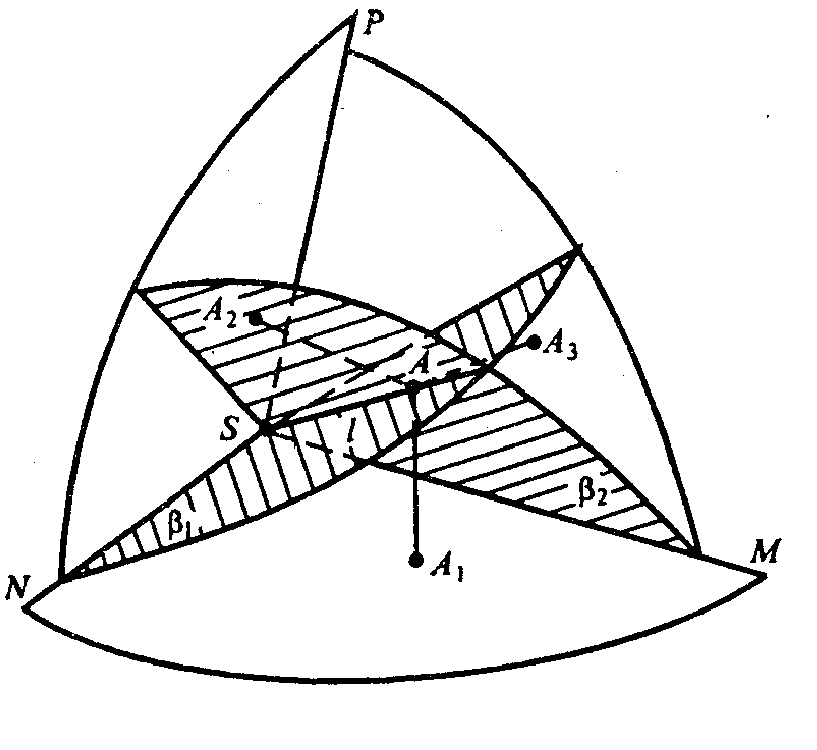
Докажем, что биссекторные плоскости двугранных углов трехгранного угла пересекаются по одному лучу.
β1 и β2 — биссекторные плоскости, их пересечение — луч, с началом в точке S — вершине тетраэдра. Луч обозначим 1. Пусть точка А ∈ l, A — произвольная точка луча. Проведем перпендикуляры АА1, АА2, АА3 на грани трехгранного угла. А ∈ β1 таким образом,
Тогда, АА1=АА2=АА3, то есть точка А равноудалена от плоскостей граней NSB и MSB. Значит, точка А находится на биссек-торной плоскости двугранного угла с ребром SP. А т.к. точка А произвольная точка, то и весь луч находится в биссекторной плоскости.
Значит, все три биссекторные плоскости пересекаются по одному лучу, любая точка которых равноудалена.
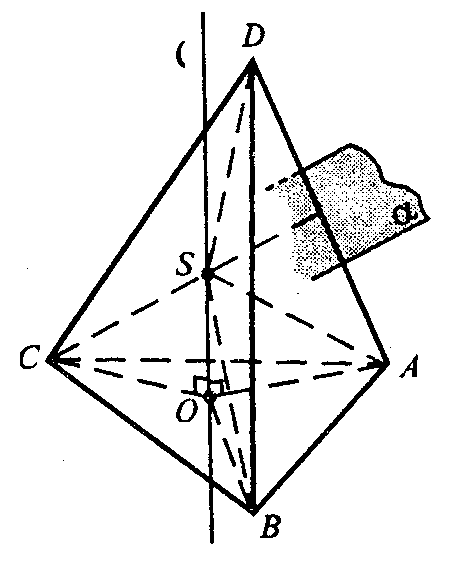
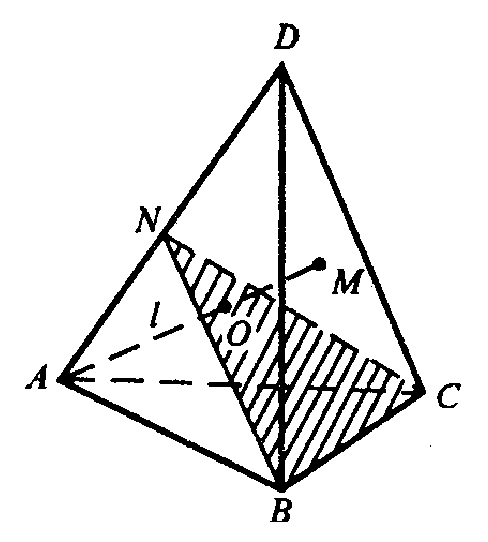
2. Пусть l — луч, по которому пересекаются биссекторные плоскости трехгранного угла при вершине А, М — точка пересечения луча l и грани BDC.
отрезка АМ принадлежат разным граням двугранного угла при ребре ВС, поэтому биссекторная плоскость этого двугранного угла пересечет отрезок АМ в точке О ∈ l, поэтому она равноудалена от плоскостей АВС и ABD и AСD. Расстояние от точки О до плоскостей АВС и BСD равны, т.к. точка О принадлежит биссекторной плоскости двугранного угла при ребре ВС. Таким образом, точка О равноудалена от всех граней тетраэдра, то есть принадлежит всем биссекторным плоскостям двугранных углов тетраэдра. Таким образом, биссекторные плоскости двугранных углов тетраэдра пересекаются в одной точке.
Оба утверждения доказаны.
638. Докажите, что: а) около любого тетраэдра можно описать сферу; б) в любой тетраэдр можно вписать сферу
Разные задачи на многогранник, цилиндр, конус и шар → номер 638
Тетраэдр — это пространственный четырехугольник.
А) Докажем, что через любые 4 точки, не лежащие в одной плоскости, можно провести сферу и притом только одну. (см. ниже).
Геометрическим местом точек пространства, равноудаленных от концов отрезка, является плоскость, перпендикулярная этому отрезку и проведенная через его середину. Следовательно, центр сферы, описанной около тетраэдра, принадлежит каждой из плоскостей, проведенных через середины ребрер тетраэдра перпендикулярно к этим ребрам.
Пусть О — центр окружности, описанной около грани АВС тетраэдра, d— прямая, которая проходит через точку О, d ⊥ плоскости АВС. Все точки прямой d равноудалены от точек А, В и С. (ОА=ОВ=ОС=r — радиус описанной окружности). Если точка S ∈ d, то прямоугольные треугольники SOA, SOB, SOC равны двум катетам. Следовательно, SA=SB=SC.
Пусть плоскость α проходит через середину ребра DA и плоскость α ⊥ DA. Докажем, что d и α пересекаются. Предположим, что α || d.
Если α ⊥ AD и d ||α, то AD ⊥ d. Кроме того, d ⊥ АВ (поскольку d ⊥ плоскости АВС), и, значит d ⊥ ABD — по признаку перпендикулярности прямой плоскости.
Таким образом, через точку А проведены две различные плоскости АВС и АВD, перпендикулярные к одной прямой, что невозможно. Значит предположение, что d || α неверно.
Значит, пусть точка S точка пересечения d и α. Тогда SD=SA, т. к. S принадлежит каждой плоскости, проходящей через середину ребра тетраэдра и перпендикуляра к этому ребру.
Пусть точка О равноудаленна от всех вершин тетраэдра.
Расстояние от точки О до одной из вершин тетраэдра обозначим R. Сфера с центром О и радиусом R проходит через все данные точки. Из этого доказательства следует, что такая сфера может быть только одна.
Что и требовалось доказать. б) Рассмотрим двугранный угол. Геометрическое место точек, равноудаленных от обеих граней двугранного угла, это плоскость, которая делит двугранный угол пополам. Значит центр сферы, вписанной в тетраэдр, равноудален от всех граней пирамиды, и он должен принадлежать каждой из биссекторных плоскостей, то есть это точка пересечения биссекторных плоскостей всех двугранных углов тетраэдра. Т. к. все точки биссекторной плоскости лежат между гранями двугранного угла, то центр сферы, вписанной в тетраэдр, всегда находится внутри тетраэдра.
Центр у вписанной сферы может быть только один. Сфера с радиусом, равным расстоянию от этой точки до плоскости какой-либо грани тетраэдра, касается всех граней тетраэдра. Следовательно, в любой тетраэдр можно вписать сферу и притом только одну.
Теперь докажем 2 факта, которые использовались в доказательстве.
1) В любой трехгранный угол можно вписать сферу.
2) Биссекторные плоскости двугранных углов тетраэдра пересекаются в одной точке.
∠AСB — линейный угол двугранного угла между плоскостями α и β.
Пусть γ делит этот двугранный угол так, что ∠BСМ=∠АСМ. Таким образом, γ биссекторная плоскость данного двугранного угла.
Докажем, что биссекторные плоскости двугранных углов трехгранного угла пересекаются по одному лучу.
β1 и β2 — биссекторные плоскости, их пересечение — луч, с началом в точке S — вершине тетраэдра. Луч обозначим 1. Пусть точка А ∈ l, A — произвольная точка луча. Проведем перпендикуляры АА1, АА2, АА3 на грани трехгранного угла. А ∈ β1 таким образом,
АА2=АА1 ; А ∈ β2, поэтому АА3=АА1.
Тогда, АА1=АА2=АА3, то есть точка А равноудалена от плоскостей граней NSB и MSB. Значит, точка А находится на биссек-торной плоскости двугранного угла с ребром SP. А т. к. точка А произвольная точка, то и весь луч находится в биссекторной плоскости.
Значит, все три биссекторные плоскости пересекаются по одному лучу, любая точка которых равноудалена.
2. Пусть l — луч, по которому пересекаются биссекторные плоскости трехгранного угла при вершине А, М — точка пересечения луча l и грани BDC.
Отрезка АМ принадлежат разным граням двугранного угла при ребре ВС, поэтому биссекторная плоскость этого двугранного угла пересечет отрезок АМ в точке О ∈ l, поэтому она равноудалена от плоскостей АВС и ABD и AСD. Расстояние от точки О до плоскостей АВС и BСD равны, т. к. точка О принадлежит биссекторной плоскости двугранного угла при ребре ВС. Таким образом, точка О равноудалена от всех граней тетраэдра, то есть принадлежит всем биссекторным плоскостям двугранных углов тетраэдра. Таким образом, биссекторные плоскости двугранных углов тетраэдра пересекаются в одной точке.
Задания
Задание
Шар и сфера, их сечения
Доказать, что около любого тетраэдра можно описать сферу и в любой тетраэдр можно вписать сферу.
а) См. Рис.1
Будем доказывать, что через любые 4 точки, не лежащие в одной плоскости, можно провести сферу, и притом только одну. Центр сферы, описанной около тетраэдра, должен принадлежать каждой из плоскостей, проведённых через середины рёбер тетраэдра перпендикулярно к его рёбрам.
Пусть О – центр окружности, описанной около грани АВС, l – прямая, проходит через О и перпендикулярна плоскости АВС. Каждая точка l равноудалена от точек А, В, С. (ОА = ОВ = ОС = r – радиус описанной окружности). Если S лежит на l, то ∆SOA = ∆SOB = ∆SOC (по двум катетам). Значит, SA = SB = SC.
Пусть плоскость α проходит через середину DA и перпендикулярна DA. Нужно доказать, что l и α пересекаются. Предположим, что это не так, т.е. что они параллельны.
Если α ⊥AD и l || α, то AD ⊥l. Но l ⊥AB и, тогда, l ⊥ABD (по признаку перпендикулярности прямой плоскости).
Значит, через одну точку были проведены две разные плоскости, перпендикулярные к одной прямой. Наше предположение неверно, т.е. l и α пересекаются. Пусть S – их точка пересечения. Тогда SD = SA. Т.к. S лежит на l, то SA = SB = SC, и, следовательно, S равноудалена от всех вершин тетраэдра.
Обозначим через R расстояние от О до одной из вершин тетраэдра. Сфера с центром в S и радиусом R проходит через все данные точки. Из доказанного выше следует, что такая сфера может быть только одна.
Таким образом, доказали, что около любого тетраэдра можно описать сферу
б) Будем рассматривать 2 грани с общим ребром. Геометрическим местом точек, равноудалённых от обеих граней двугранного угла, будет плоскость, делящая двугранный угол пополам, или, другими словами, биссекторная плоскость этого двугранного угла. Поэтому центр сферы, вписанной в тетраэдр, равноудалён от всех граней пирамиды, он принадлежит каждой из биссекторных плоскостей, т.е. он – точка пересечения биссекторных плоскостей всех двугранных углов тетраэдра. Центр сферы, вписанной в тетраэдр, всегда находится внутри тетраэдра, т.к. все точки биссекторной плоскости расположены между гранями двугранного угла.
Таким образом, центр у вписанной сферы может быть только один. Сфера с центром в этой точке и радиусом, равным расстоянию от этой точки до плоскости какой-либо грани тетраэдра, касается всех граней тетраэдра. Значит, в любой тетраэдр можно вписать сферу и притом только одну.
Осталось лишь доказать, что биссекторные плоскости двугранных углов тетраэдра пересекаются в одной точке.
См. Рис.2
M лежит на γ. Угол АСВ – линейный угол двугранного угла между плоскостями α и β.
Пусть γ делит этот угол так, что углы ВСМ и АСМ равны, т.е. γ – биссекторная плоскость. Докажем, что биссекторные плоскости двугранных углов трёхгранного угла пересекаются по одному лучу.
См. Рис.3
β1 и β2 – биссекторные плоскости, их пересечение – луч l, исходящий из вершины S тетраэдра. Пусть А, принадлежащая l, произвольная точка луча. Проведём перпендикуляры AA1, AA2, AA3 на грани трёхгранного угла. A принадлежит β1, поэтому АА2 = AA1; A принадлежит β2, поэтому АА3 = AA1.
Значит AA1 = AA2 = AA3, т.е. А равноудалена от плоскостей граней NSP и MSP. Значит, А находится на биссеторной плоскости двугранного угла с ребром SP. Т.к. мы выбирали А произвольно, значит, весь луч находится в биссекторной плоскости. Значит, все три биссекторные плоскости пересекаются по одному лучу, любая точка которых равноудалена.
См. Рис.4
Пусть l – луч, по которому пересекаются биссекторные плоскости трёхгранного угла при вершине А, М – точка, в которой l пересекает BDC. Концы АМ принадлежат разным граням двугранного угла при ребре ВС, поэтому биссекторная плоскость этого двугранного угла пересечёт отрезок АМ в точке О. О лежит на l, поэтому она равноудалена от плоскостей ABC, ABD и ACD. Кроме этого, расстояние от О до ABC и BCD равны, т.к. О принадлежит биссекторной плоскости двугранного угла при ребре ВС. Значит, О равноудалена от всех граней тетраэдра, т.е. принадлежит всем биссекторным плоскостям двугранных углов тетраэдра. Итак, биссекторные плоскости двугранных углов тетраэдра пересекаются в одной точке.
Сфера, описанная около тетраэдра.
Известно, что около всякого тетраэдра можно описать сферу, её центр O лежит на перпендикулярах к граням тетраэдра, восстановленных в центрах окружностей, описанных около граней.
Медианы тетраэдра.
Отрезок, соединяющий вершину тетраэдра с центроидом противоположной грани, называется медианой тетраэдра. Свойства медиан тетраэдра аналогичны свойствам медиан треугольника.
Теорема 4. Четыре медианы тетраэдра ABCD пересекаются в одной точке G, которая делит каждую из них в отношении 3:1, считая от вершины тетраэдра, причем
где P – любая точка пространства.
Доказательство. Возьмем на медиане DG’тетраэдра ABCD точку G, определяемую соотношением DG : GG’ = 3 : 1 ( рис 5). Согласно формуле (1),
Учитывая, что центроид G’ треугольника ABC удовлетворяет соотношению 3PG = PA + PB + PC, получим
Вычисляя вектор PG’’ с концом в точке G’’, делящей любую из трех других медиан тетраэдра в отношении 3 : 1 (считая от вершины), получим то же самое выражение. А это означает, что все четыре медианы тетраэдра пересекаются в одной точке G, удовлетворяющей соотношению (4). Точка G, называется
центром тяжести (или центроидом) тетраэдра.
Высоты тетраэдра.
Высоты треугольника всегда пересекаются в одной точке. По аналогии можно предположить, что высоты любого тетраэдра также пересекаются в одной точке. Однако это не так.
Для примера рассмотрим тетраэдр ABCD с прямым двугранным углом при ребре AB, в котором AC = BC, но AD = BD (рис. 6). Высоты CE и DF тетраэдра лежат соответственно в гранях ABC и ABD, но точка E – середина AB, а F – нет. Если бы длины ребер DA и DB были равны, то основания E и F совпадали бы, но две другие высоты тетраэдра не могут проходить через точку E.
Таким образом, даже две высоты тетраэдра могут не иметь общей точки.
Тем не менее существуют и тетраэдры, все четыре высоты которых пересекаются в одной точке. Таким будет, например, тетраэдр ABCD с прямыми плоскими углами при вершине D. Ребра DA, DB и DC являются его высотами, а вершина D – ортоцентром(точкой пересечения всех четырех высот).
Попробуем найти все тетраэдры, у которых высоты пересекаются в одной точке.
Пусть высоты тетраэдра ABCD, проведенные из вершин C и D, пересекаются в точке H
( рис. 7). Тогда CH’__AB и DH’’__AB, т.е. прямая AB перпендикулярна к двум пересекающимся прямым лежащим в плоскости CDH, следовательно, AB__BC. Аналогично доказывается, что если две другие высоты тетраэдра ABCD проходят через ту же точку H, то AC__BD и AD__BC. Итак, если все высоты тетраэдра пересекаются в одной точке, то противоположные ребра тетраэдра взаимно перпендикулярны. Такой тетраэдр называется ортоцентрическим.
Теорема 5. Четыре высоты ортоцентрического тетраэдра ABCD пересекается в одной точке H, причем если O – центр сферы, описанной около тетраэдра, то
Доказательство. Пусть ABCD – ортоцентрический тетраэдр, DG’ – его медиана, DH’ – его высота (рис.8). Тогда G’ центроид, а H’- ортоцентр треугольника ABC, причем точки O’( центр окружности, описанной около треугольника ABC), G’ и H’ лежат на одной прямой. Заметим, что центр O сферы, описанной около тетраэдра ABCD, лежит на перпендикуляре к плоскости треугольника ABC, восстановленном в точке O’.
Будем доказывать теорему тем же способом, что и теорему 2 для треугольника: строить разными способами точку H, удовлетворяющую соотношению (5).
Вначале сложим векторы OA, OB и OC:
или G’M = 2OG’. Точки O’,G’,H’, лежат на прямой Эйлера треугольника ABC, причем H’G’ = 2G’O’. Следовательно,
Отсюда вытекает, что прямые H’M и OO’ параллельны, а так как прямая OO’ перпендикулярна к плоскости ABC, то и прямая H’M перпендикулярна к этой плоскости. Следовательно, точка M’ лежит на прямой DH’ ( если точки O и O’ совпадают, то точки M и H’ тоже совпадают).
Из левого равенства следует, что точка H является серединой отрезка DM, т.е. точка H лежит на DH’ тетраэдра.
Следовательно, высоты ортоцентрического тетраэдра пересекаются в одной точке H, определяемой соотношением (5).
Прямая Эйлера тетраэдра.
Теорема 6. Центр О описанной сферы, центроид G и ортоцентр Н ортоцентрического тетраэдра ABCD лежат на одной прямой, причем точки О и Н симметричны относительно точки G.
Доказательство. По формулам (4) и (5)
откуда OH=2OG. Полученное равенство означает, что точки O, G, H лежат на одной прямой, причем точки О и Н симметричны относительно точки G.
Прямую, на которой лежат точки O, G, H, можно назвать прямой Эйлера ортоцентрического тетраэдра.
В данном реферате собран материал необходимый для выявления прямой Эйлера и прямой Эйлера тетраэдра.
Использованные источники информации:
Сфера, описанная около тетраэдра.
Известно, что около всякого тетраэдра можно описать сферу, её центр O лежит на перпендикулярах к граням тетраэдра, восстановленных в центрах окружностей, описанных около граней.
Медианы тетраэдра.
Отрезок, соединяющий вершину тетраэдра с центроидом противоположной грани, называется медианой тетраэдра. Свойства медиан тетраэдра аналогичны свойствам медиан треугольника.
Теорема 4.Четыре медианы тетраэдра ABCD пересекаются в одной точке G, которая делит каждую из них в отношении 3:1,считая от вершины тетраэдра, причем
4PG = PA + PB +PC +PD, (4)
где P – любая точка пространства.
Доказательство.Возьмем на медиане DG’тетраэдра ABCD точку G, определяемую соотношением DG : GG’ = 3 : 1 (рис 5). Согласно формуле (1),
Учитывая, что центроид G’ треугольника ABC удовлетворяет соотношению 3PG = PA + PB + PC, получим
Вычисляя вектор PG’’ с концом в точке G’’, делящей любую из трех других медиан тетраэдра в отношении 3 : 1 (считая от вершины), получим то же самое выражение. А это означает, что все четыре медианы тетраэдра пересекаются в одной точке G, удовлетворяющей соотношению (4). Точка G, называется
центром тяжести (или центроидом) тетраэдра.
Высоты тетраэдра.
Высоты треугольника всегда пересекаются в одной точке. По аналогии можно предположить, что высоты любого тетраэдра также пересекаются в одной точке. Однако это не так.
Для примера рассмотрим тетраэдр ABCD с прямым двугранным углом при ребре AB, в котором AC = BC, но AD = BD (рис. 6). Высоты CE и DF тетраэдра лежат соответственно в гранях ABC и ABD, но точка E – середина AB, а F – нет. Если бы длины ребер DA и DB были равны, то основания E и F совпадали бы, но две другие высоты тетраэдра не могут проходить через точку E.
Таким образом, даже две высоты тетраэдра могут не иметь общей точки.
Тем не менее существуют и тетраэдры, все четыре высоты которых пересекаются в одной точке. Таким будет, например, тетраэдр ABCD с прямыми плоскими углами при вершине D. Ребра DA, DB и DC являются его высотами, а вершина D – ортоцентром(точкой пересечения всех четырех высот).
Попробуем найти все тетраэдры, у которых высоты пересекаются в одной точке.
Пусть высоты тетраэдра ABCD, проведенные из вершин C и D, пересекаются в точке H
(рис. 7). Тогда CH’__AB и DH’’__AB, т.е. прямая AB перпендикулярна к двум пересекающимся прямым лежащим в плоскости CDH, следовательно, AB__BC. Аналогично доказывается, что если две другие высоты тетраэдра ABCD проходят через ту же точку H, то AC__BD и AD__BC. Итак, если все высоты тетраэдра пересекаются в одной точке, то противоположные ребра тетраэдра взаимно перпендикулярны. Такой тетраэдр называется ортоцентрическим.
Теорема 5.Четыре высоты ортоцентрического тетраэдра ABCD пересекается в одной точке H, причем если O – центр сферы, описанной около тетраэдра, то
Доказательство.Пусть ABCD – ортоцентрический тетраэдр, DG’ – его медиана, DH’ – его высота (рис.8). Тогда G’ центроид, а H’- ортоцентр треугольника ABC, причем точки O’(центр окружности, описанной около треугольника ABC), G’ и H’ лежат на одной прямой. Заметим, что центр O сферы, описанной около тетраэдра ABCD, лежит на перпендикуляре к плоскости треугольника ABC, восстановленном в точке O’.
Будем доказывать теорему тем же способом, что и теорему 2 для треугольника: строить разными способами точку H, удовлетворяющую соотношению (5).
Вначале сложим векторы OA, OB и OC:
OM = OA + OB + OC.
По теореме 1
OM = 3OG’
или G’M = 2OG’. Точки O’,G’,H’, лежат на прямой Эйлера треугольника ABC, причем H’G’ = 2G’O’. Следовательно,
Отсюда вытекает, что прямые H’M и OO’ параллельны, а так как прямая OO’ перпендикулярна к плоскости ABC, то и прямая H’M перпендикулярна к этой плоскости. Следовательно, точка M’ лежит на прямой DH’ (если точки O и O’ совпадают, то точки M и H’ тоже совпадают).
Из левого равенства следует, что точка H является серединой отрезка DM, т.е. точка H лежит на DH’ тетраэдра.
Следовательно, высоты ортоцентрического тетраэдра пересекаются в одной точке H, определяемой соотношением (5).